本記事では、音声データをMFCC(メル周波数ケプストラム係数)で特徴量抽出する方法を解説します。
ケプストラムとあるように、基本的理解にはケプストラム分析の概念が必要です。そちらの解説記事も書いていますので、ぜひご覧ください。
【Python】音声の特徴量抽出MFCCの前段階:ケプストラム分析
MFCCの概要
MFCCは次のようにして求めます。
1. 音声をフーリエ変換して周波数領域にする
2. メル尺度で周波数領域を変換し、フィルタバンクで周波数の情報を圧縮(メルフィルタバンク)
3. 対数パワースペクトルに変換
4. 離散コサイン変換し、ケフレンシー領域で低周波数と高周波数に分離
MFCCではメルフィルタバンクとケプストラム分析のそれぞれを理解する必要があります。
フィルタバンク
フィルタバンクとは、入力信号を分解するフィルタのことです。
重要な信号は密に取り、重要でない信号は比較的大雑把に取ります。今回のメルフィルタバンクの例でもそうですが、フィルタバンクを取ることで周波数情報を圧縮することが可能です。
音声認識ではどのようなフィルタバンクを設計すればよいか?ということが疑問になりますが、MFCCではメル(mel) と呼ばれる尺度を使います。厳密な数式の定義は後に説明するとして、メル尺度は、人間の音高の知覚的尺度ということを理解しておけば大丈夫です。
メル尺度を用いたフィルタバンクのことをメルフィルタバンク といいます。
上記の順番では、メルフィルタバンクは2. に当てはまります。
2. メル尺度で周波数領域を変換し、フィルタバンクで周波数の情報を圧縮(メルフィルタバンク)
メルフィルタバンクによる周波数領域の圧縮
他の記事と差別化を図るためにも…、ということでメル尺度について深堀していこうと思います。
音高を知覚的尺度にするメル尺度ですが、周波数$f$から次のように求められます。また逆変換の式も記載します。
m = m_o \log\left(\frac{f}{f_o} + 1\right), \hspace{10pt}f = f_o\left(\exp\frac{m}{m_o}-1\right)
ここで意外に重要なのは、周波数パラメータ $f_o$です。既存の論文だと、$f_o$=700 Hz, 1000 Hzなどがあります。
周波数パラメータの性質があり、
・$f<<f_o$だと、周波数成分とメル尺度は比例する。
・$f>>f_o$だと、メル尺度に対して周波数成分は指数的に増加する。逆変換の式を参照。
となります。
グラフで表現してみます。メル尺度に対する周波数は次の通りになります。
※プログラムでメル尺度を等間隔で取る都合上、以下では逆変換の式を用いていることをご了承ください。
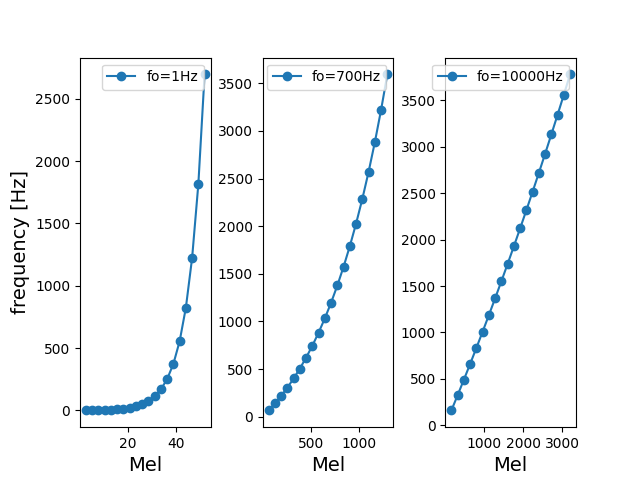
図を見てもらうとわかるように、$f>>f_o$であるほど、低周波数を取る数が多くなります。
$f_o$= 700 Hzの場合、メルフィルタバンクは次のようになります。三角形の頂点部分が取得する周波数になります。

メルフィルタバンク上で見てみても、$f_o$= 700 Hzでも低周波数側が密に取られていることがわかります。
ケプストラム分析
ケプストラム分析 にあたるのは3.~4.の部分です。
3. 対数パワースペクトルに変換
4. 離散コサイン変換し、ケフレンシー領域で低周波数と高周波数に分離
ケプストラム分析でMFCCを解釈すると、
1.で1回目のフーリエ変換→3. 周波数領域の対数パワーに変換→4.の2回目のフーリエ変換でケフレンシー領域
という手順がなされていることがわかります。
あくまで3.の時点ですが、元の周波数とメルフィルタバンクで圧縮された対数パワースペクトルが比較できます。
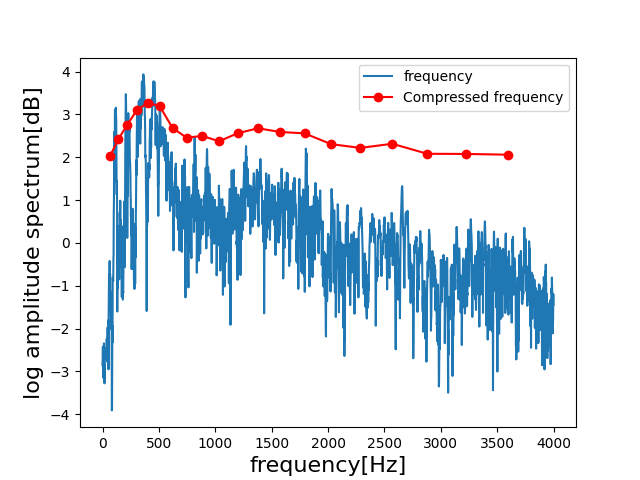
ケプストラム分析によれば、ケフレンシーの低次元を取るとスペクトル包絡が取得できます。
このスペクトル包絡の情報が重要であれば、圧縮する際に低次元をフィルタバンクで多くとります。そして、スペクトル微細成分は荒く取り、MFCCを構成します。
実数値を取らなければいけないのでMFCCではフーリエ変換ではなく、離散コサイン変換を使います。
MFCCのプログラム
MFCCを初心者が追うとかなり苦労します。初心者の方は、一度ケプストラム分析から振り返るとよいと思います。
※アルゴリズム上では音声に窓関数をかける必要がありますが、窓関数にもたくさん種類がありますので一意にプログラムを作成できません。そのため、窓関数については割愛します。
1. 音声データをFFTする
dft = np.abs(np.fft.fft(self.data))[:int(N/2)]
ナイキスト周波数を考慮し、データを半分にします。
2. メルフィルタバンクを作成する
今回メルフィルタバンクはクラスを作成しました。その際、コンストラクタを次のようにしています。
class MelFilterBankCalc:
"""
Class for calculate mel-filterbank.
To calculate, call the melfilterbank fucntion.
Attributes:
N: Data length.
fs: samplingrate
fo: frequency Parameter. Default setting is 700.
mel: Definition of the mel scale. Default setting is 1000.
numChannels: Specifying the number of bandpass fileters. Default setting is 20.
"""
def __init__(self, N, fs, fo=700, mel=1000, numChannels=20):
self.N = N
self.fs = fs
self.fo = fo
self.mel = mel
self.numChannels = numChannels
コメントにも書いていますが、メンバ変数は次の通り。
N: データ長
fs: サンプリングレート
fo: 周波数パラメータ
mel: 周波数パラメータから導かれる従属パラメータを求めるための初期値
numChannels: 周波数領域を圧縮する次元数
melを解説していませんでしたが、下記でも扱うように$f_o$の従属パラメータ$m_o$を求めるための初期値です。
2-1. メル尺度と周波数を相互に変換する
以下も、MelFilterBankCalcクラスの一部になります。変換式はメル尺度の定義によるものと、その逆変換式になります。
def calc_mo(self):
"""
Functions for determining dependent parameters of the Mel scale.
"""
return self.mel / np.log((self.mel / self.fo) + 1.0)
def hz2mel(self, f):
"""
Convert Hz to mel.
"""
mo = self.calc_mo()
return mo * np.log(f / self.fo + 1.0)
def mel2hz(self, m):
"""
Convert mel to Hz
"""
mo = self.calc_mo()
return self.fo * (np.exp(m / mo) - 1.0)
2-2.メルフィルタバンクを作成する
率直なところ、厄介です。時間をかけて、プログラムを一行ずつ追っていくとよいと思います。
def melfilterbank(self):
"""
Calculate mel-fileterbank.
Returns:
filterbank: (numChannels, N) matrix.
fcenters: Frequency of bandpass filtering.
"""
fmax = self.fs / 2 #Nyquist frequency
melmax = self.hz2mel(fmax) #Mel scale of Nyquist frequency
Nmax = int(self.N / 2) #Maximum frequency index
df = self.fs / self.N #Frequency resolution
dmel = melmax / (self.numChannels + 1)
melcenters = np.arange(1, self.numChannels + 1) * dmel #Center frequency of each filter on the Mel scale
fcenters = self.mel2hz(melcenters) #Converts the center frequency of each filter ot Hz
indexcenter = np.round(fcenters / df) #Convert the center frequency of each filter to freuency indexes
indexstart = np.hstack(([0], indexcenter[0:self.numChannels - 1]))
indexstop = np.hstack((indexcenter[1:self.numChannels], [Nmax]))
filterbank = np.zeros((self.numChannels, Nmax))
for channel in np.arange(0, self.numChannels):
#Find the point from the slope of the straight line to the left of the triangular fileter
increment = 1.0 / (indexcenter[channel] - indexstart[channel])
for i in np.arange(indexstart[channel], indexcenter[channel]):
filterbank[int(channel), int(i)] = (i - indexstart[channel]) * increment
#Find the point from the slope of the straight line to the right of the triangular filete
decrement = 1.0 / (indexstop[channel] - indexcenter[channel])
for j in np.arange(indexcenter[channel], indexstop[channel]):
filterbank[int(channel), int(j)] = 1.0 - ((j - indexcenter[channel]) * decrement)
return filterbank, fcenters
概要としては大まかにわけて次の二つです。
・メル尺度を等間隔に取り、周波数に変換する。fcentersまでがそれに該当。
・それ以降は、フィルタバンクを作成するためのプログラム
これによりnumChannel×データ長/2 のデータ配列が完成します。numChannel=20, データ長が8192だとすると、20×4096行列が取得できます。
2-3. メルフィルタバンクを実データに適用し、圧縮する
melfileterbank_obj = MelFilterBank.MelFilterBankCalc(N, self.fs)
filterbank, fcenters = melfileterbank_obj.melfilterbank()
inner_product_fbank = np.dot(dft, filterbank.T)
ここからは、MelFilterBankCalcクラスから外れます。
MelFilterBankCalcクラスをオブジェクト化し、フィルタバンクを出力します。
そして、inner_product_fbankが圧縮のプログラムに相当します。 先人かしこい。
3. 対数パワースペクトルに変換する
mspec = np.log10(inner_product_fbank)
対数パワースペクトルに変換します。
※このとき、$f >> f_o$でinner_product_fbankの要素が0を取る場合があります。まとめで紹介するGitHubのソースコードには修正プログラムを入れています。
4. 離散コサイン変換し、低次元部を取り出す
import scipy.fftpack.realtransforms
cutpont = 12
ceps = scipy.fftpack.realtransforms.dct(mspec, norm="ortho")
output_ceps = ceps[1:cutpoint + 1]
対数パワースペクトルをケフレンシー領域に変換します。また低次元を取り出す数値も設定します。numChannels=20のうち、12個を取り出すということが多いです。
以上で、12次元のMFCCによる特徴量抽出が完了しました。
【結果】サポートベクトルマシンによる正解率【機械学習】
ようやく音声の特徴量を抽出できるようになりました。早速、機械学習にかけてみます。
MFCCでは通常、SVM(サポートベクトルマシン)に入力するのが常套手段 のようです。今回は簡易のため、線形SVMにかけてみます。
今回使用した音声のデータセットとその結果
今回のデータセットは、Attribution-ShareAlike 4.0 International (CC BY-SA 4.0)のJakobovskiらによるFree Spoken Digit Datasetを使用しました。
【GitHub】 free-spoken-digit-dataset
6人のスピーカーが0~9の音声を約1秒間だけ発する音声が収録されており、上記のGitHubよりダウンロードできます。
結果ですが、正解率は83.6% となりました。高いか低いかなど議論の余地がありますが、経験上の正解率は確保できているように思います。
結果については、次のソースコードで再現可能です。
上記のデータセットをダウンロードして、指定のファイルパスに置いて次のGitHubのlinearSVM.pyを実行すると、同様の結果が得られます。
【GitHub】MFCC linearSVM TEST
まとめ:GitHubに公開中
誤解を恐れずにいうと、MFCCを求めるプログラムは10年前のとある記事から量産されており、私もそれに乗っかっている一人です。
その記事が、いつ消えてしまうかわかりません。別の方がOSSを残し、残しておくことが重要ではないかと思います。
次の記事を拝見したところ、近年では離散コサイン変換を省いたメルスペクトラムでディープラーニングにかけるようです。時間があるときに論文を拝見し、試してみようと思います。
参考: 【Qiita】MFCC(メル周波数ケプストラム係数)入門
最後に、MFCCを求めるプログラムを誰でも使えるようMITライセンスでGitHubを上げています。
実行時、できるだけバグを検出し、汎用性のあるプログラムを作成したつもりです。どうぞご利用ください。
【GitHub】MFCC (Mel-frequency cepstrum coefficients)