音声の特徴量抽出はMFCC(メル周波数ケプストラム係数)をよく見かけます。しかし、メル周波数ケプストラム係数は名前に含まれているようにケプストラム(Cepstrum) と呼ばれる分析方法が基本にあります。
今回は、ケプストラム分析とPythonで書いたソースコードを解説をします。特にケプストラムの基本とソースコードについて着目するつもりですので、厳密な定義などは省きます。
ケプストラム分析とその注目すべき点
ケプストラム(cepstrum) 分析とは音声信号処理において周波数スペクトルを信号とみなして、フーリエ変換する手法 のことです。
これだけ聞くと通常は「何いってるのん??」となります。ケプストラム分析をするメリットとしては、スペクトル包絡と、スペクトル微細変動成分に分離できる点です。
試したものが以下になります。
今回の音声ファイルはAttribution-ShareAlike 4.0 International (CC BY-SA 4.0)のJakobovskiらによるFree Spoken Digit Datasetを使用しました。
【Github】 free-spoken-digit-dataset
6人のスピーカーが0~9の音声を約1秒間だけ発する音声で構成されており、上記からダウンロードすることができます。
今回は、0と発している音声のファイルを指定しています。
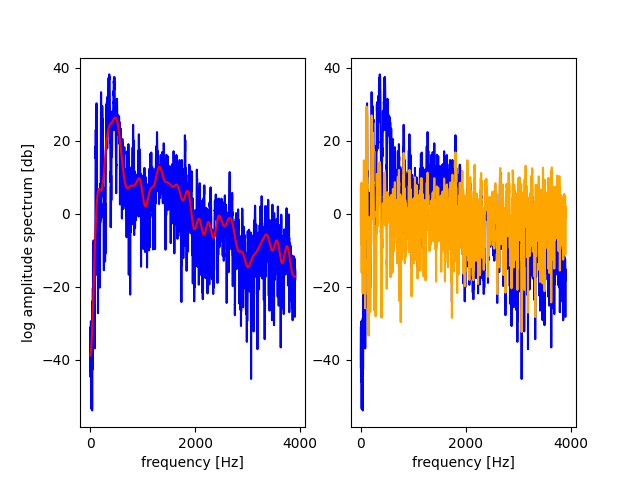
両図の青色のグラフは元信号のスペクトル。左図の赤色のグラフはケプストラムで抽出したスペクトル包絡。細かい変動成分がなくなって、包絡成分が抽出されていることがわかります。
また右図のオレンジ色のグラフはスペクトル微細成分です。包絡成分がなくなり、細かい変動成分のみになっていることがわかります。
分離するためには、スペクトル包絡とスペクトル微細成分が足し算になっていることが必要です。周波数領域ではこれらが積になっています。
数式に例えると次の通りです。ここがケプストラム分析の重要な点 です。
周波数領域のある信号$X(f)$に対して、便宜上2つの信号$F(f), G(f)$があるとし、周波数領域では
X(f) = F(f)G(f)
と仮定します。両辺に対数を取ると、
\log|X(f)| = \log|F(f)| + \log|G(f)|
となり、和の形を取ることができるため分離できるというわけです。
このため、ケプストラム分析によるスペクトラム包絡の分離は対数パワースペクトルを取る必要があります。
アルゴリズム的には次のようになります。音声データをフーリエ変換し、さらにフーリエ変換するというのが特徴です。
1. 音声データ
2. 周波数領域 (1. をフーリエ変換)
3. 対数パワースペクトル
4. ケフレンシー領域 (3. をフーリエ変換。逆フーリエ変換を取る流儀が多いですが、上記の理論は変わりません。)
5. 対数パワースペクトル (4.をフーリエ変換)
ケフレンシー(quefrency) とは、対数パワースペクトルをフーリエ変換した領域のことで、時間尺度に相当します。しかし、周波数領域を(逆)フーリエ変換したものではないので、信号の時間領域とは異なります。
深い意味は考えず、ケフレンシーは対数パワースペクトルをフーリエ変換したものなんだと理解 していいと思います。
4.から5.にかけて、リフタ(lifter) とよばれるケフレンシー領域でのフィルタをかけます。ローパスフィルタやハイパスフィルタに相当するフィルタをかけてあげると、5. の時点でスペクトル包絡とスペクトル微細成分が取得できます。
では実際にソースコードを書いていきます。
ケプストラム分析のソースコードを解説
アルゴリズムを見てもらうとわかるように、フーリエ変換のライブラリさえあれば、ケプストラム分析は可能です。リフタをかけてスペクトル包絡か微細成分を抽出できますが、今回紹介するのはスペクトル包絡です。
今回の実行環境は次の通りです。
Python 3.8.1
Ubuntu 20.04.4 LTS
numpy 1.21.4
1. 音声データの読み込み
今回は音声処理を行うPythonライブラリのsoundfileを使用します。
import soundfile
fname = '0_jackson_0.wav' #Any wav file.
data, fs = soundfile.read(fname)
音声ファイルパスを指定し、音声データとサンプリングレートを抽出します。
今回の音声データの波形は次の通りです。
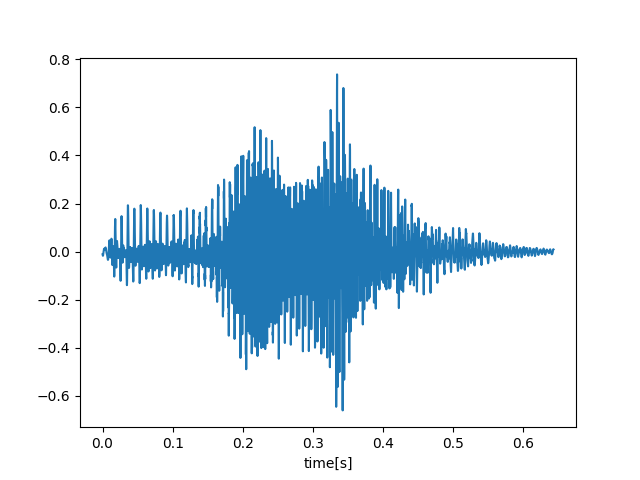
2. 周波数領域へのフーリエ変換
次にフーリエ変換によって、音声データを周波数領域に変換します。今回はnumpyパッケージのフーリエ変換関数を使います。
n = len(data)
fscale = np.linspace(0, fs, n)
dft = np.fft.fft(data, n)
またグラフ化するときに、周波数領域のデータ配列も必要ですので、numpyのlinspace()でサンプリングレート分だけ作成します。
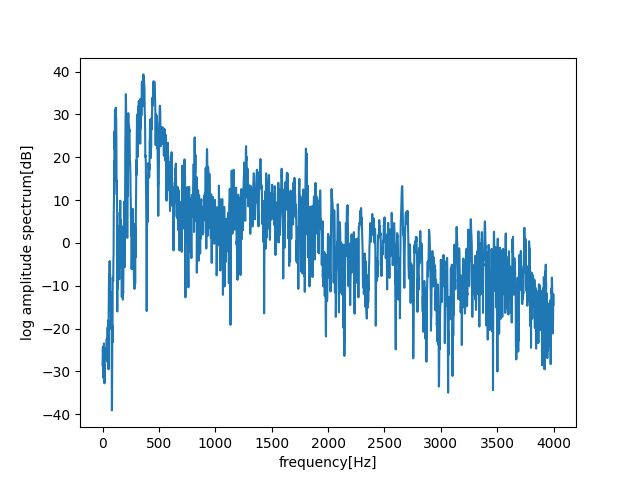
3. 対数パワースペクトルへの変換
dft_abs = np.abs(dft)
LogAmpDFT = 10*np.log10(dft_abs**2)
対数パワースペクトルに変換します。対数の性質上、真数>0ですので、絶対値にします。
そして、基準を$1^2$としてデシベルの定義に変換します。
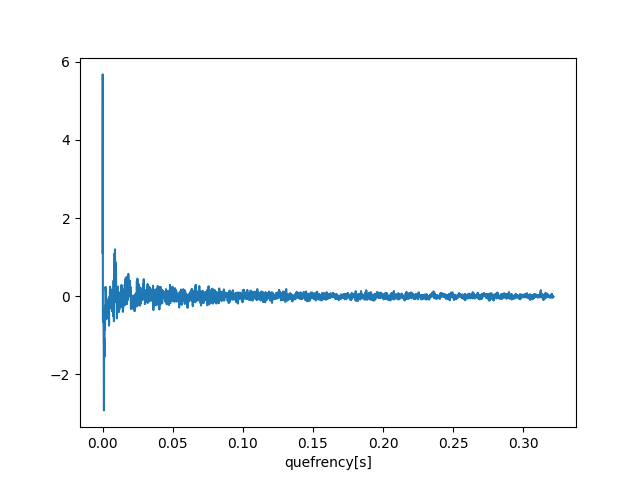
4. ケフレンシー領域
次にケフレンシー領域に変換します。今回は逆フーリエ変換の流儀を使います。
cps = np.real(np.fft.ifft(LogAmpDFT))
逆フーリエ変換して可視化するときは実数値にします。このデータ配列がケフレンシーになりますので、次でリフタをかけてスペクトル包絡を抽出します。
4. (補足) ケフレンシー領域でのリフタ
cpsCoef = index #index=50に指定
cps[cpsCoef:len(cps) - cpsCoef] = 0
今回はケフレンシーのデータ配列の高次元部分を0に指定します。低次元と高次元の比は0.018 (=50/5148)ですので、高次元と呼ぶデータ配列部分は非常に多いことに注意してください。
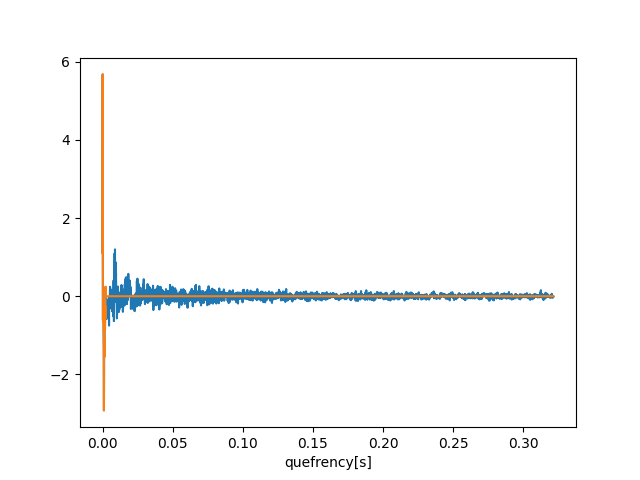
オレンジ色がローパスリフタで残した部分です。残りは0になっています。
また初心者が引っかかりやすいのですが、データ配列の両サイドのデータは残すことです。
具体的には、今回の場合データ長が5148個ですので配列番号50~5098を0にします。
今回はスペクトル包絡の場合ですが、スペクトル微細成分を取る場合は低次元部分を0にすればよいです。
5. 対数パワースペクトルの再変換
dft_cps_low = np.real(np.fft.fft(cps, n))
最後に対数パワースペクトルに再変換にします。ローパスリフタをかけているので、スペクトル包絡が得られます。
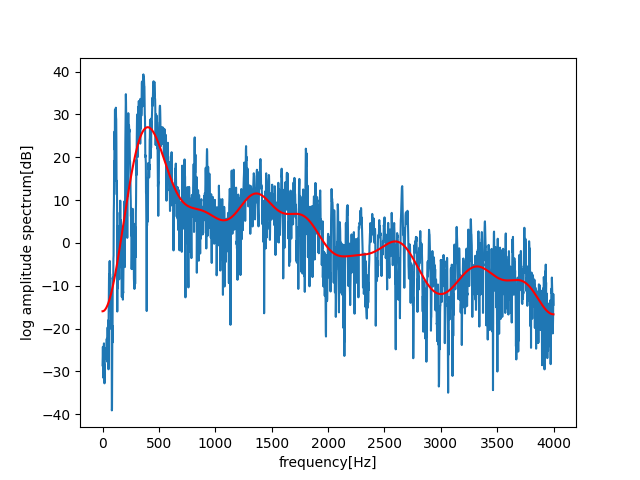
赤色のグラフがスペクトル包絡です。元スペクトルの包絡線を抽出できていることがわかります。
まとめ:GitHubに公開中
これにて、ケプストラム分析が可能になりました。この考え方が基本となり、MFCCで音声の特徴量抽出が可能になります。
また音声データからスペクトル包絡とスペクトル微細成分それぞれを抽出するソースコードをGitHubに公開しています。
音声データとサンプリングレートを指定するだけで、ケプストラム分析が可能です。ぜひ利用してみてください。
