前々回に行った第二量子化Hamiltonianの係数計算は、「Psi4」や「PySCF」という量子化学計算パッケージによって行うことも可能です。
前回用いた「OpenFermion (参考論文 : arXiv)」は、これらのパッケージと接続することで、第二量子化Hamiltonianの構成・Bravyi-Kitaev変換・基底状態の決定(Hamiltonian行列の厳密対角化)、までを一気通貫で行うことができます。
今回は、OpenFermionおよびPsi4を用いて
「Scalable Quantum Simulation of Molecular Energies」(PRX 2016)
(https://journals.aps.org/prx/abstract/10.1103/PhysRevX.6.031007)
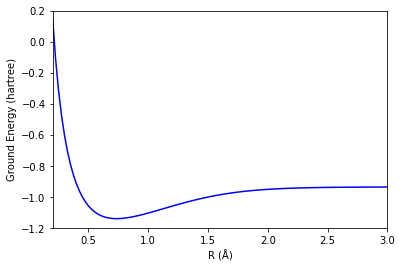
論文の数値計算結果(H$_2$分子の全エネルギー曲面)を再現します。
やること
・Psi4のインストール
・OpenFermion-Psi4のインストール
・H$_2$分子の基底エネルギー計算
Psi4のインストール
[公式サイト](http://psicode.org/)のdownloadsからインストーラーをダウンロード出来ます。
注意点として、Macユーザーはある程度古い(?)モデルの場合に、下の「OLD HDW」の方を選択する必要があるようです : [Report problems with 1.1 installers](http://forum.psicode.org/t/report-problems-with-1-1-installers/520/14
) 。自分はこのインストールミスによるエラーで2日ぐらい消えました...。ターミナルで`psi4 --test`を実行してテスト計算が始まればインストール成功です。上記のようなミスをしていると、`Illegal Instruction 4`とかいうエラーが表示されます。
OpenFermion-Psi4のインストール
「OpenFermion-Psi4」というプラグインによって、OpenFermionとPsi4を接続します。
公式GitHubに従ってインストールを行いました。
OpenFermion-Psi4の実行
まずは、計算したい分子系のパラメータを指定します。
geometryで分子構造、
basisで基底関数、
multiplicityは全スピン$S$とした時の$2S+1$(今回はsingleの基底状態なので$S=0$)、
chargeに電荷(イオン化していなければ$0$)、
descriptionには保存するファイル名
を指定します。
これらをMolecularData関数で１つのデータとしてまとめたものをmolecule変数に渡します。
from openfermion.hamiltonians import MolecularData
geometry = [["H", [0,0,0]],
["H", [0,0,0.7414]]]
basis = "sto-3g"
multiplicity = 1
charge = 0
description = "test" #str()
molecule = MolecularData(geometry, basis, multiplicity, charge, description)
ここから、Openfermion-psi4を通してPsi4を実行し、計算結果を取得します。run_psi4という関数でOpenfermionからPsi4を実行出来ます。
from openfermionpsi4 import run_psi4
from openfermion.transforms import get_fermion_operator, jordan_wigner, bravyi_kitaev
molecule = run_psi4(molecule)
print(molecule.get_molecular_hamiltonian())
bk_hamiltonian = bravyi_kitaev(get_fermion_operator(molecule.get_molecular_hamiltonian()))
print(bk_hamiltonian)
moleculeオブジェクトからインスタンスを指定することで結果を呼び出すことができます。
この例では、.get_molecular_hamiltonian()によってFermion operatorでのHamiltonianが自動構成されています。
さらに、前回行ったBravyi-Kitaev変換を続けて行うことで、qubit operatorでのHamiltonianが得られました。前回の結果とほぼ一致しています($\mathrm I$の係数については、定数項の分だけ差が生じています)。
Output
() 0.713753990544915
((0, 1), (0, 0)) -1.252463571592775
((1, 1), (1, 0)) -1.252463571592775
((2, 1), (2, 0)) -0.4759487172683108
((3, 1), (3, 0)) -0.4759487172683108
((0, 1), (1, 1), (1, 0), (0, 0)) 0.33724438286695113
((0, 1), (1, 1), (3, 0), (2, 0)) 0.09064440419713071
((0, 1), (2, 1), (0, 0), (2, 0)) 0.09064440419713077
((0, 1), (2, 1), (2, 0), (0, 0)) 0.3317340479282188
((0, 1), (3, 1), (1, 0), (2, 0)) 0.09064440419713077
((0, 1), (3, 1), (3, 0), (0, 0)) 0.3317340479282188
((1, 1), (0, 1), (0, 0), (1, 0)) 0.33724438286695113
((1, 1), (0, 1), (2, 0), (3, 0)) 0.09064440419713071
((1, 1), (2, 1), (0, 0), (3, 0)) 0.09064440419713077
((1, 1), (2, 1), (2, 0), (1, 0)) 0.3317340479282188
((1, 1), (3, 1), (1, 0), (3, 0)) 0.09064440419713077
((1, 1), (3, 1), (3, 0), (1, 0)) 0.3317340479282188
((2, 1), (0, 1), (0, 0), (2, 0)) 0.33173404792821903
((2, 1), (0, 1), (2, 0), (0, 0)) 0.0906444041971309
((2, 1), (1, 1), (1, 0), (2, 0)) 0.33173404792821903
((2, 1), (1, 1), (3, 0), (0, 0)) 0.0906444041971309
((2, 1), (3, 1), (1, 0), (0, 0)) 0.09064440419713096
((2, 1), (3, 1), (3, 0), (2, 0)) 0.34869688341114197
((3, 1), (0, 1), (0, 0), (3, 0)) 0.33173404792821903
((3, 1), (0, 1), (2, 0), (1, 0)) 0.0906444041971309
((3, 1), (1, 1), (1, 0), (3, 0)) 0.33173404792821903
((3, 1), (1, 1), (3, 0), (1, 0)) 0.0906444041971309
((3, 1), (2, 1), (0, 0), (1, 0)) 0.09064440419713096
((3, 1), (2, 1), (2, 0), (3, 0)) 0.34869688341114197
(-0.09886397351781719+0j) [] +
(0.17119774853325845+0j) [Z0] +
(0.17119774853325845+0j) [Z0 Z1] +
(-0.22278592890106907+0j) [Z2] +
(-0.22278592890106913+0j) [Z1 Z2 Z3] +
(0.16862219143347557+0j) [Z1] +
(0.04532220209856542+0j) [Y0 Z1 Y2 Z3] +
(0.04532220209856542+0j) [X0 Z1 X2] +
(0.04532220209856542+0j) [X0 Z1 X2 Z3] +
(0.04532220209856542+0j) [Y0 Z1 Y2] +
(0.12054482186554402+0j) [Z0 Z2] +
(0.16586702396410946+0j) [Z0 Z1 Z2 Z3] +
(0.16586702396410946+0j) [Z0 Z1 Z2] +
(0.12054482186554402+0j) [Z0 Z2 Z3] +
(0.17434844170557098+0j) [Z1 Z3]
OpenFermionではさらに、qubit mapされたHamiltonianを自動で疎行列表示に翻訳し、対角化から基底エネルギーの導出を行ってくれます。
from openfermion.transforms import get_sparse_operator
from openfermion.utils import get_ground_state
sparse_operator = get_sparse_operator(bk_hamiltonian)
print(sparse_operator, "\n")
print(get_ground_state(sparse_operator)[0])
output
(0, 0) (0.7137539905449151+0j)
(1, 1) (0.23780527327660436+0j)
(2, 2) (0.45925032283057743+0j)
(8, 2) (0.18128880839426167+0j)
(3, 3) (0.23780527327660425+0j)
(4, 4) (-0.5324790108539945+0j)
(5, 5) (-0.5387095810478599+0j)
(6, 6) (-0.35119020245973287+0j)
(12, 6) (-0.18128880839426167+0j)
(7, 7) (0.3524341345564165+0j)
(2, 8) (0.18128880839426167+0j)
(8, 8) (-1.1166843869067329+0j)
(9, 9) (-0.4469857208564294+0j)
(10, 10) (0.9201067120161576+0j)
(11, 11) (-0.4469857208564296+0j)
(6, 12) (-0.18128880839426167+0j)
(12, 12) (-0.35119020245973276+0j)
(13, 13) (-0.5387095810478599+0j)
(14, 14) (-0.5324790108539946+0j)
(15, 15) (0.3524341345564164+0j)
-1.137270174625323
H2分子のエネルギー曲面
ここまでのコードをまとめ上げて、各ボンド長に対する計算を行うことでエネルギー曲面が書けます。
from openfermion.hamiltonians import MolecularData
from openfermionpsi4 import run_psi4
from openfermion.transforms import get_fermion_operator, jordan_wigner, bravyi_kitaev, get_sparse_operator
from openfermion.utils import get_ground_state
import matplotlib.pyplot as plt
%matplotlib inline
def get_Energy(bond_length):
geometry = [["H", [0,0,0]], ["H", [0,0,bond_length]]]
basis = "sto-3g"
multiplicity = 1
charge = 0
description = str(round(bond_length, 2))
molecule = MolecularData(geometry, basis, multiplicity, charge, description)
# run Psi4
molecule = run_psi4(molecule) #, run_mp2 = True, run_cisd = True, run_ccsd = True, run_fci = True)
bk_hamiltonian = bravyi_kitaev(get_fermion_operator(molecule.get_molecular_hamiltonian()))
sparse_operator = get_sparse_operator(bk_hamiltonian)
return get_ground_state(sparse_operator)[0]
initial = 0.20
step = 0.025
number = 28*4+1
data1 = []
data2 = []
for i in range(number):
bond_length = initial + i*step
data1.append(bond_length)
temp = get_Energy(bond_length)
data2.append(temp)
#print(bond_length, temp)
# 図にプロット
plt.plot(data1,data2,"blue")
plt.xlabel("R (Å)")
plt.ylabel("Ground Energy (hartree)")
plt.xlim(0.20,3.00)
plt.ylim(-1.2,0.2)
plt.legend()
plt.show
論文図とだいたい一致しています！