$$
\def\bra#1{\mathinner{\left\langle{#1}\right|}}
\def\ket#1{\mathinner{\left|{#1}\right\rangle}}
\def\braket#1#2{\mathinner{\left\langle{#1}\middle|#2\right\rangle}}
$$
量子化学計算における量子計算アルゴリズム「VQE(量子固有値変分法ソルバー)」を実装する際に、PyQuanteによる数値計算が必要になったのでメモを残しておきます。
VQEは「Scalable Quantum Simulation of Molecular Energies」(PRX 2016)(https://journals.aps.org/prx/abstract/10.1103/PhysRevX.6.031007)
を参照し、この論文の数値計算結果(H$_2$分子の全エネルギー)を再現することを目的としました。
この記事では、VQEアルゴリズムで必要となる、Hamiltonian中に含まれる係数の具体的な値(論文中のTable Ⅲ、Bravyi-Kitaev変換前)を数値計算により導出する部分のみを扱います。計算ツールとしては、論文に準じてPyQuante 1.6.3を使用します。(PyQuanteはチュートリアルや解説記事が少ないため非常に苦戦しました)
やること
電子系のHamiltonian
\begin{eqnarray}
\mathcal{H} &=& - \sum_{i} \frac{\nabla^2_{R_i}}{2M_i} - \sum_{i} \frac{\nabla^2_{r_i}}{2} - \sum_{i,j} \frac{Z_i}{|R_i-r_j|} + \sum_{i,j>i} \frac{Z_i Z_j}{|R_i - R_j|} + \sum_{i,j>i} \frac{1}{|r_i-r_j|}\\
\end{eqnarray}
これをBorn-Oppenheimier近似の下で第二量子化した次の表式
\begin{eqnarray}
\mathcal{H}(R) &=& \sum_{p,q} h_{pq} c^{\dagger}_p c_q + \frac{1}{2} \sum_{p,q,r,s} h_{pqrs} c^{\dagger}_p c^{\dagger}_q c_r c_s + \sum_{i,j>i} \frac{Z_i Z_j}{|R_i - R_j|}
\end{eqnarray}
における係数$h_{pq}$と$h_{pqrs}$を数値計算します。この係数は何らかの基底関数系{$\phi_i ({\bf r})$}を用いて、
\begin{eqnarray}
h_{pq} &=& \int \phi^{*}_p({\bf r}) \left( -\frac{\nabla^2_{{\bf r}}}{2} - \sum_{i} \frac{Z_i}{|R_i-{\bf r}|} \right) \phi_q({\bf r}) \, d{\bf r} \\
h_{pqrs} &=& \iint \frac{1}{|{\bf r_1}-{\bf r_2}|} \phi^{*}_p({\bf r_1}) \phi^{*}_q({\bf r_2}) \phi_r({\bf r_2}) \phi_s({\bf r_1}) \, d{\bf r_1} d{\bf r_2} \\
\end{eqnarray}
のように書ける。
水素分子
基底関数系{$\phi_i ({\bf r})$}として分子軌道を用います。分子軌道は各原子の原子軌道を重ね合わせて構成したものです。具体的に、片方のH原子の1s軌道を$\psi_1(r)$、もう片方を$\psi_2(r)$とおくと、
(画像)
\begin{eqnarray}
\phi_g (r) &=& c_{11} \psi_1(r) + c_{12} \psi_2(r) \\
\phi_u (r) &=& c_{21} \psi_1(r) + c_{22} \psi_2(r) \\
\end{eqnarray}
通常、係数$c_{ij}$を求めるためには、Hartree-Fock近似したHamiltonianで基底状態を探すことを行う。今回のような等核2原子分子の場合には次のような簡単な形になることが知られている。(この時点では規格化されていないので注意)
\begin{eqnarray}
\phi_g (r) &=& \psi_1(r) + \psi_2(r) \\
\phi_u (r) &=& \psi_1(r) - \psi_2(r)
\end{eqnarray}
(例)$h_{gg}$を計算
\begin{eqnarray}
h_{gg} &=& \int d{\bf r} \, \phi^{*}_g({\bf r}) \left( -\frac{\nabla^2_{{\bf r}}}{2} - \sum_{i} \frac{Z_i}{|R_i-{\bf r}|} \right) \phi_g({\bf r})\\
&=& \int d{\bf r} \, \left( \psi^{*}_1({\bf r}) + \psi^{*}_2({\bf r}) \right) U_1({\bf r}) \left( \psi_1({\bf r}) + \psi_2({\bf r}) \right) \\
&=& \int \psi^{*}_1({\bf r}) U_1({\bf r})\psi_1({\bf r}) d{\bf r} + \int \psi^{*}_1({\bf r}) U_1({\bf r})\psi_2({\bf r}) d{\bf r} + \int \psi^{*}_2({\bf r}) U_1({\bf r})\psi_1({\bf r}) d{\bf r} + \int \psi^{*}_2({\bf r}) U_1({\bf r})\psi_2({\bf r}) d{\bf r} \nonumber
\end{eqnarray}
真ん中のポテンシャル項を$U_1({\bf r})$と略した。
PyQuanteによる計算 (1)
具体的にPyQuanteによる数値計算コードを見ていきます。PyQuanteを公式サイトに従ってインストールします。(注意点として、PyQuanteはpython2系にのみ対応しています。)
チュートリアルにあるように、次のコードによってH$_2$分子を構成出来ます。分子名'H2'(適当で大丈夫っぽいです)、原子名'H'(原子番号で指定も出来ます)、座標位置(0, 0, 0)と(0, 0, 1.4)、長さの単位(=Angstrom)という情報をh2 の変数に代入しています。
import PyQuante
from PyQuante.Molecule import Molecule
h2 = Molecule('H2',
[('H', (0.00000000, 0.00000000, 0.00000000)),
('H', (0.00000000, 0.00000000, 1.40000000))],
units='Angstrom')
次のように変数solverに計算方法を指定してやれば、数値計算を行うことが出来ます。この例ではSCF計算により全エネルギーを計算しています。
import PyQuante
from PyQuante.Molecule import Molecule
from PyQuante import SCF
h2 = Molecule('H2',
[('H', (0.00000000, 0.00000000, 0.00000000)),
('H', (0.00000000, 0.00000000, 0.70000000))],
units='Angstrom')
solver = SCF(h2,method="HF",basis="sto-3g")
solver.iterate()
print solver.energy
-1.11734902288
PyQuanteによる計算 (2)
実際に係数を数値計算してみましょう。
from PyQuante.Molecule import Molecule
from PyQuante import Ints
atoms = Molecule('H2',
[(1, (0.00000000, 0.00000000, 0.00000000)),
(1, (0.00000000, 0.00000000, 0.74140000))],
units='Angstrom')
bfs = Ints.getbasis(atoms,'sto-3g')
S = Ints.getS(bfs) # the overlap matrix S
T = Ints.getT(bfs) # the kinetic energy matrix T
V = Ints.getV(bfs, atoms) # the nuclear attraction matrix V
print "S : \n", S
print "T : \n", T
print "V : \n", V
S :
[[ 1. 0.65895716]
[ 0.65895716 1. ]]
T :
[[ 0.76003188 0.236126 ]
[ 0.236126 0.76003188]]
V :
[[-1.88008306 -1.19385827]
[-1.19385827 -1.88008306]]
解説
Ints.getbasis(atoms,'sto-3g')で、H原子の1s軌道をSTO-3G基底で表現する処理を行います(基底関数系(化学)_wikipedia)。試しに、print bfs[0], bfs[1]でSTO-3G基底を表示してみると
<cgbf atomid=0 origin="(0.000000,0.000000,0.000000)" powers="(0,0,0)">
<prim exp="3.4253" coeff="0.1543" ncoeff="0.2769"/>
<prim exp="0.6239" coeff="0.5353" ncoeff="0.2678"/>
<prim exp="0.1689" coeff="0.4446" ncoeff="0.0835"/>
</cgbf>
<cgbf atomid=1 origin="(0.000000,0.000000,1.401043)" powers="(0,0,0)">
<prim exp="3.4253" coeff="0.1543" ncoeff="0.2769"/>
<prim exp="0.6239" coeff="0.5353" ncoeff="0.2678"/>
<prim exp="0.1689" coeff="0.4446" ncoeff="0.0835"/>
</cgbf>
確かに、1つの原子軌道が原子核を中心としたガウス関数3つの重ね合わせとなっていることがわかります。
次にbfsをInts.getS()、Ints.getT()、Ints.getV()などの関数に放り込みます。これらの関数は自動で、重なり積分、運動エネルギー項、原子核ポテンシャル項を計算してくれます。例えば、
\begin{eqnarray}
S_{11} &=& \int \psi^{*}_1({\bf r}) \, \psi_1({\bf r}) d{\bf r} \\
T_{12} &=& \int \psi^{*}_1({\bf r}) \left( -\frac{\nabla^2_{{\bf r}}}{2} \right)\psi_2({\bf r}) d{\bf r} \\
V_{21} &=& \int \psi^{*}_2({\bf r}) \left( - \sum_{i} \frac{Z_i}{|R_i-{\bf r}|} \right) \psi_1({\bf r}) d{\bf r}
\end{eqnarray}
これらを用いて、求めたかった係数を導出します。
係数計算
(例)$h_{gg}$を計算
規格化因子$\sigma_g, \sigma_u$まで含めた式は、次のようになります。
\begin{eqnarray}
h_{gg} &=& \int \frac{\phi^{*}_g({\bf r})}{\sigma_g} \left( -\frac{\nabla^2_{{\bf r}}}{2} - \sum_{i} \frac{Z_i}{|R_i-{\bf r}|} \right) \frac{\phi_g({\bf r})}{\sigma_g} \, d{\bf r} \\
&=& \frac{1}{\sigma^2} \int d{\bf r} \, \left( \psi^{*}_1({\bf r}) + \psi^{*}_2({\bf r}) \right) \left( -\frac{\nabla^2_{{\bf r}}}{2} - \sum_{i} \frac{Z_i}{|R_i-{\bf r}|} \right) \left( \psi_1({\bf r}) + \psi_2({\bf r}) \right) \\
&=& \frac{1}{\sigma^2} \left( T_{11}+T_{12}+T_{21}+T_{22} + V_{11}+V_{12}+V_{21}+V_{22} \right) \\
\end{eqnarray}
ここで、規格化因子$\sigma_g, \sigma_u$は
\begin{eqnarray}
\sigma_g^2 &=& \int \phi^{*}_g({\bf r}) \, \phi_g({\bf r}) \, d{\bf r} \\
&=& \int \left( \psi^{*}_1({\bf r}) + \psi^{*}_2({\bf r}) \right) \, \left( \psi_1({\bf r}) + \psi_2({\bf r}) \right) \, d{\bf r}\\
&=& S_{11}+S_{12}+S_{21}+S_{22} \\
\sigma_u^2 &=& \int \phi^{*}_u({\bf r}) \, \phi_u({\bf r}) \, d{\bf r} \\
&=& \int \left( \psi^{*}_1({\bf r}) - \psi^{*}_2({\bf r}) \right) \, \left( \psi_1({\bf r}) - \psi_2({\bf r}) \right) \, d{\bf r}\\
&=& S_{11}-S_{12}-S_{21}+S_{22} \\
\end{eqnarray}
実際に数値計算すると、
print ((T[0,0] + T[0,1] + T[1,0] + T[1,1]) + (V[0,0] + V[0,1] + V[1,0] + V[1,1])) / (S[0,0] + S[0,1] + S[1,0] + S[1,1])
-1.25246359983
論文の結果($h_{00} =− 1.252477$)とほぼ一致している。
他の係数も同様にして、次のコードによって計算される。
import math
import numpy as np
from PyQuante.Molecule import Molecule
from PyQuante import Ints
atoms = Molecule('H2',
[(1, (0.00000000, 0.00000000, 0.00000000)),
(1, (0.00000000, 0.00000000, 0.74140000))],
units='Angstrom')
bfs = Ints.getbasis(atoms,'sto-3g')
print bfs[0], bfs[1]
S = Ints.getS(bfs) # the overlap matrix S
T = Ints.getT(bfs) # the kinetic energy matrix T
V = Ints.getV(bfs, atoms) # the nuclear attraction matrix V
print "S : \n", S
print "T : \n", T
print "V : \n", V
print ((T[0,0] + T[0,1] + T[1,0] + T[1,1]) + (V[0,0] + V[0,1] + V[1,0] + V[1,1])) / (S[0,0] + S[0,1] + S[1,0] + S[1,1])
normalize_g_square = S[0,0] + S[0,1] + S[1,0] + S[1,1]
normalize_u_square = S[0,0] - S[0,1] - S[1,0] + S[1,1]
a = np.zeros((2,2))
a[0,0] = ((T[0,0] + T[0,1] + T[1,0] + T[1,1]) + (V[0,0] + V[0,1] + V[1,0] + V[1,1])) / normalize_g_square
a[0,1] = ((T[0,0] - T[0,1] + T[1,0] - T[1,1]) + (V[0,0] - V[0,1] + V[1,0] - V[1,1])) / math.sqrt(normalize_g_square*normalize_u_square)
a[1,0] = ((T[0,0] + T[0,1] - T[1,0] - T[1,1]) + (V[0,0] + V[0,1] - V[1,0] - V[1,1])) / math.sqrt(normalize_g_square*normalize_u_square)
a[1,1] = ((T[0,0] - T[0,1] - T[1,0] + T[1,1]) + (V[0,0] - V[0,1] - V[1,0] + V[1,1])) / normalize_u_square
print "h : \n", a
h :
[[-1.2524636 0. ]
[ 0. -0.4759487]]
注意点
ここまでスピン関数については無視していましたが、スピンまで考慮した拡張は簡単に出来ます。スピンまで含めた基底関数{$,\chi_p({\bf r},\sigma)$}を
\begin{eqnarray}
\ket{\chi_0} = \ket{\phi_g} \ket{\alpha} \\
\ket{\chi_1} = \ket{\phi_g} \ket{\beta} \\
\ket{\chi_2} = \ket{\phi_u} \ket{\alpha} \\
\ket{\chi_3} = \ket{\phi_u} \ket{\beta}
\end{eqnarray}
のように定義すると、
(例) $h_{00}$の表式
\begin{eqnarray}
h_{00} &=& \sum_{\sigma} \int d{\bf r} \, \chi^{*}_0({\bf r},\sigma) \left( -\frac{\nabla^2_{{\bf r}}}{2} - \sum_{i} \frac{Z_i}{|R_i-{\bf r}|} \right) \chi_0({\bf r},\sigma) \\
&=& \sum_{\sigma} \int d{\bf r} \, \phi^{*}_g({\bf r}) \alpha(\sigma) \left( -\frac{\nabla^2_{{\bf r}}}{2} - \sum_{i} \frac{Z_i}{|R_i-{\bf r}|} \right) \phi_g({\bf r}) \alpha(\sigma) \\
&=& \int d{\bf r} \, \phi^{*}_g({\bf r}) \left( -\frac{\nabla^2_{{\bf r}}}{2} - \sum_{i} \frac{Z_i}{|R_i-{\bf r}|} \right) \phi_g({\bf r}) \\
&=& h_{gg} \\
\end{eqnarray}
のようになります。
ちなみに、スピン関数$\ket{\alpha}$と$\ket{\beta}$は直交するので$h_{01}$や$h_{34}$などは0になります。さらに、$\phi_g$と$\phi_u$も直交するように分子軌道を構成したので$h_{02}$なども0となる。結局非ゼロの係数は$h_{00},h_{11},h_{22},h_{33}$の4つのみであり、$h_{00}=h_{11} =h_{gg},h_{22}=h_{33} =h_{uu}$となる。これで一体積分項については論文を再現出来た。
PyQuanteによる計算 (3)
次は2体ポテンシャル項$h_{pqrs}$の計算をします。
\begin{eqnarray}
h_{pqrs} &=& \iint \frac{1}{|{\bf r_1}-{\bf r_2}|} \phi^{*}_p({\bf r_1}) \phi^{*}_q({\bf r_2}) \phi_r({\bf r_2}) \phi_s({\bf r_1}) \, d{\bf r_1} d{\bf r_2}
\end{eqnarray}
まずは次のコードで事前計算をします。
from PyQuante.Molecule import Molecule
from PyQuante import Ints
atoms = Molecule('H2',
[(1, (0.00000000, 0.00000000, 0.00000000)),
(1, (0.00000000, 0.00000000, 0.74140000))],
units='Angstrom')
bfs = Ints.getbasis(atoms, 'sto-3g')
S, h, ints = Ints.getints(bfs, atoms)
pre_h = [ints[i] for i in range(len(ints))]
print pre_h
[0.7746059413378763, 0.4437931823313278, 0.29666320701323484, 0.5694684210929628, 0.44379318233132775, 0.7746059413378763]
二体積分としてInts.getints()関数を使っています。この関数によって、次の表式で表わされる原子軌道間の積分値が返って来ます。
\begin{eqnarray}
h^{'}_{pqrs} &=& \iint \frac{1}{|{\bf r_1}-{\bf r_2}|} \psi^{*}_p({\bf r_1}) \psi^{*}_q({\bf r_2}) \psi_r({\bf r_2}) \psi_s({\bf r_1}) \, d{\bf r_1} d{\bf r_2}
\end{eqnarray}
ここから少し煩雑になるのでブラケット表記し、分母項も省略します。
\begin{eqnarray}
h^{'}_{pqrs} &=& \bra{p} \braket{q}{r} \ket{s} \\
&=& \braket{p}{s} \braket{q}{r} \\
\end{eqnarray}
$h^{'}$が取りうる値のバリエーションについて考えると、$p,q,r,s = 1,2$なので
\begin{eqnarray}
\braket{1}{1} \braket{1}{1} &=& h^{'}_{1111} \\
\braket{2}{1} \braket{1}{1} &=& h^{'}_{2111} = h^{'}_{1211} = h^{'}_{1121} = h^{'}_{1112} \\
\braket{2}{1} \braket{2}{1} &=& h^{'}_{2121} = h^{'}_{2112} = h^{'}_{1221} = h^{'}_{1212} \\
\braket{2}{2} \braket{1}{1} &=& h^{'}_{2211} = h^{'}_{1122} \\
\braket{2}{2} \braket{2}{1} &=& h^{'}_{2221} = h^{'}_{2212} = h^{'}_{2122} = h^{'}_{1222} \\
\braket{2}{2} \braket{2}{2} &=& h^{'}_{2222} \\
\end{eqnarray}
の6通りしかないことがわかる。上のコードでは、この順番でそれぞれの積分値がpre_hに代入されています。この$h^{'}$から、求めたかった係数$h_{pqrs}$が計算出来ます。
(例)$h_{gggg}$
\begin{eqnarray}
h_{gggg} &=& \braket{g}{g} \braket{g}{g} \\
&=& (\bra{1}+\bra{2}) (\ket{1}+\ket{2}) \, (\bra{1}+\bra{2}) (\ket{1}+\ket{2}) \\
&=& h^{'}_{1111} + 4 h^{'}_{2111} + 4h^{'}_{2121} + 2h^{'}_{2211} + 4h^{'}_{2221} + h^{'}_{2222}
\end{eqnarray}
規格化因子も考慮して、次のコードで計算出来る。
import numpy as np
from PyQuante.Molecule import Molecule
from PyQuante import Ints
atoms = Molecule('H2',
[(1, (0.00000000, 0.00000000, 0.00000000)),
(1, (0.00000000, 0.00000000, 0.74140000))],
units='Angstrom')
bfs = Ints.getbasis(atoms,'sto-3g')
S, h, pre_h = Ints.getints(bfs,atoms)
normalize_g_square = S[0,0] + S[0,1] + S[1,0] + S[1,1]
normalize_u_square = S[0,0] - S[0,1] - S[1,0] + S[1,1]
coeff_gggg = np.array((1,4,4,2,4,1))
h_gggg = np.dot(pre_h,coeff_gggg) / (normalize_g_square * normalize_g_square)
print "h_gggg =", h_gggg
h_gggg = 0.674488773633
論文の結果($h_{0110} =− 0.674493$)とほぼ一致している。
他の$h_{pqrs}$についても計算してみる。
import numpy as np
from PyQuante.Molecule import Molecule
from PyQuante import Ints
atoms = Molecule('H2',
[(1, (0.00000000, 0.00000000, 0.00000000)),
(1, (0.00000000, 0.00000000, 0.74140000))],
units='Angstrom')
bfs = Ints.getbasis(atoms,'sto-3g')
S, h, pre_h = Ints.getints(bfs,atoms)
normalize_g = np.sqrt(S[0,0] + S[0,1] + S[1,0] + S[1,1])
normalize_u = np.sqrt(S[0,0] - S[0,1] - S[1,0] + S[1,1])
normalize = [normalize_g, normalize_u]
def calculate_h(p,q,r,s):
m = 0
coeff = np.zeros(6)
for i in range(2):
for j in range(2):
for k in range(2):
for l in range(2):
temp = str(i) + str(j)+ str(k)+ str(l)
#print temp
if temp == "0000":
m = 0
elif temp in ["1000","0100","0010","0001"]:
m = 1
elif temp in ["1010","0110","1001","0101"]:
m = 2
elif temp in ["1100","0011"]:
m = 3
elif temp in ["1110","1101","1011","0111"]:
m = 4
elif temp in ["1111"]:
m = 5
coeff[m] += ((-1)**p)**i * ((-1)**q)**j * ((-1)**r)**k * ((-1)**s)**l
temp_result = np.dot(pre_h,coeff) / (normalize[p] * normalize[q] * normalize[r] * normalize[s])
if temp_result <= 1.0e-10: # これより小さい値は誤差とみなして0にする
temp_result = 0
return temp_result
h = np.zeros((2,2,2,2))
p = 0
q = 0
r = 0
s = 0
gu = ["g","u"]
for p in range(2):
for q in range(2):
for r in range(2):
for s in range(2):
print "psqr =", gu[p], gu[q], gu[r], gu[s], " h =", calculate_h(p,q,r,s)
psqr = g g g g h = 0.674488773633
psqr = g g g u h = 0
psqr = g g u g h = 0
psqr = g g u u h = 0.663468099401
psqr = g u g g h = 0
psqr = g u g u h = 0.181288807997
psqr = g u u g h = 0.181288807997
psqr = g u u u h = 0
psqr = u g g g h = 0
psqr = u g g u h = 0.181288807997
psqr = u g u g h = 0.181288807997
psqr = u g u u h = 0
psqr = u u g g h = 0.663468099401
psqr = u u g u h = 0
psqr = u u u g h = 0
psqr = u u u u h = 0.697393764439
出て来る値は6通りのバリエーションしかなく、
\begin{eqnarray}
\braket{g}{g} \braket{g}{g} &=& 0.674488773633 \\
\braket{g}{g} \braket{u}{u} &=& 0.663468099401 \\
\braket{g}{u} \braket{g}{u} &=& 0.181288807997 \\
\braket{g}{u} \braket{g}{g} &=& 0 \\
\braket{g}{u} \braket{u}{u} &=& 0 \\
\braket{u}{u} \braket{u}{u } &=& 0.697393764439 \\
\end{eqnarray}
ここで$\braket{g}{u} \braket{g}{g}$と$\braket{g}{u} \braket{u}{u}$が0になっている理由について確認する。$\braket{g}{u} \braket{g}{g}$を本来の表式で書くと、
\begin{eqnarray}
h_{gggu} &=& \iint \frac{1}{|{\bf r_1}-{\bf r_2}|} \phi^{*}_g({\bf r_1}) \phi^{*}_g({\bf r_2}) \phi_g({\bf r_2}) \phi_u({\bf r_1}) \, d{\bf r_1} d{\bf r_2}
\end{eqnarray}
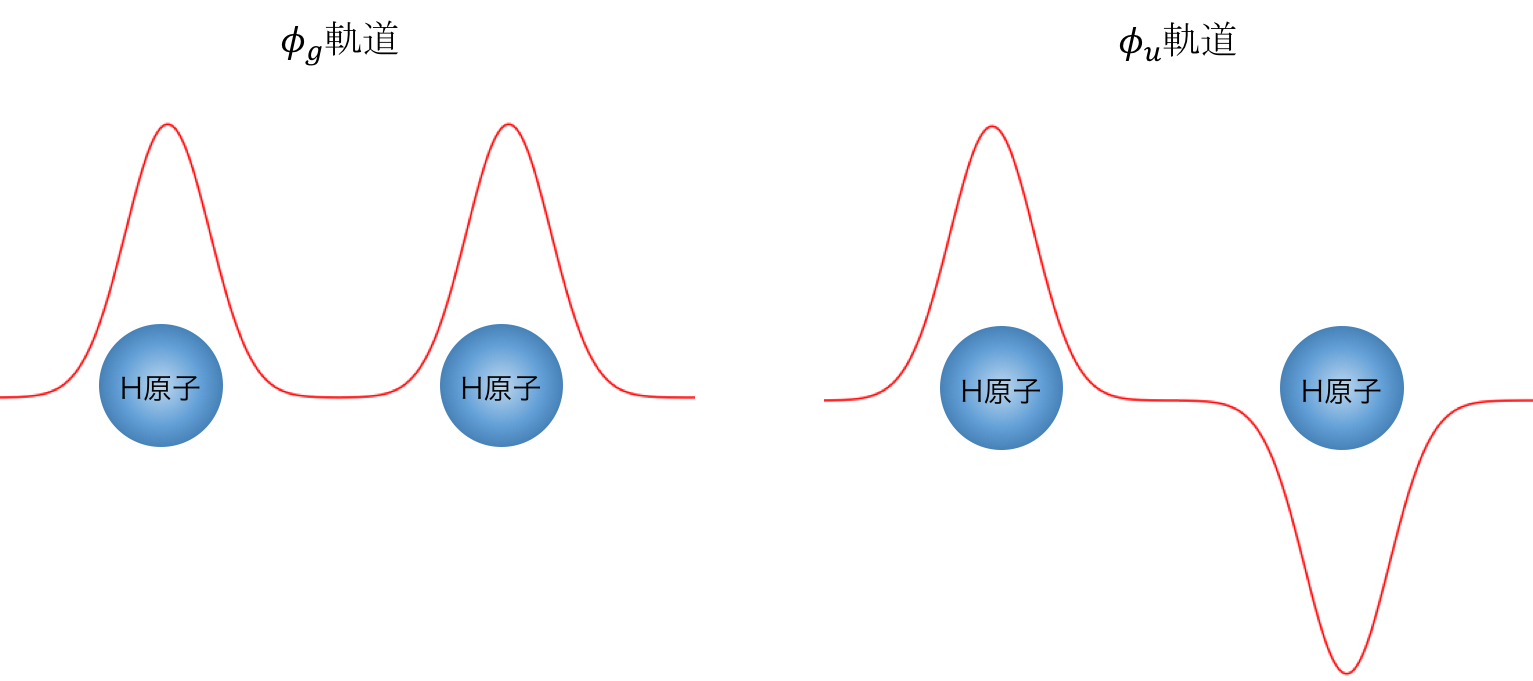
$\phi_g$は原点周りに偶関数、$\phi_u$は奇関数、$|{\bf r_1}-{\bf r_2}|$は偶関数なので、被積分関数全体としては${\bf r_1} \to -{\bf r_1}, {\bf r_2} \to -{\bf r_2}$で符号反転する奇関数である。よって積分により0となる。
スピンについて拡張
スピンまで含めた基底関数{$,\chi_p({\bf r},\sigma)$}を次のように定義します
\begin{eqnarray}
\ket{0} = \ket{\phi_g} \ket{\alpha} \\
\ket{1} = \ket{\phi_g} \ket{\beta} \\
\ket{2} = \ket{\phi_u} \ket{\alpha} \\
\ket{3} = \ket{\phi_u} \ket{\beta}
\end{eqnarray}
スピン関数の直交性により、0とならない内積は$\braket{0}{0},\braket{0}{2},\braket{2}{0},\braket{2}{2},\braket{1}{1},\braket{1}{3},\braket{3}{1},\braket{3}{3}$の8つである。よって$\braket{p}{s}\braket{q}{r}$の組み合わせは全部で64通りである。

この内、生成消滅演算子$c_p^{\dagger} c_q^{\dagger} c_r c_s$について、Fermion生成消滅演算子の性質により、$p=q, r=s$のいずれかが満たされる場合は必ず0となる(Pauliの排他律および真空に対する消滅演算子の作用)。0になる項を除くと、

$h_{pqrs}$として項を表現すると、(0の項はそのまま0と表記)
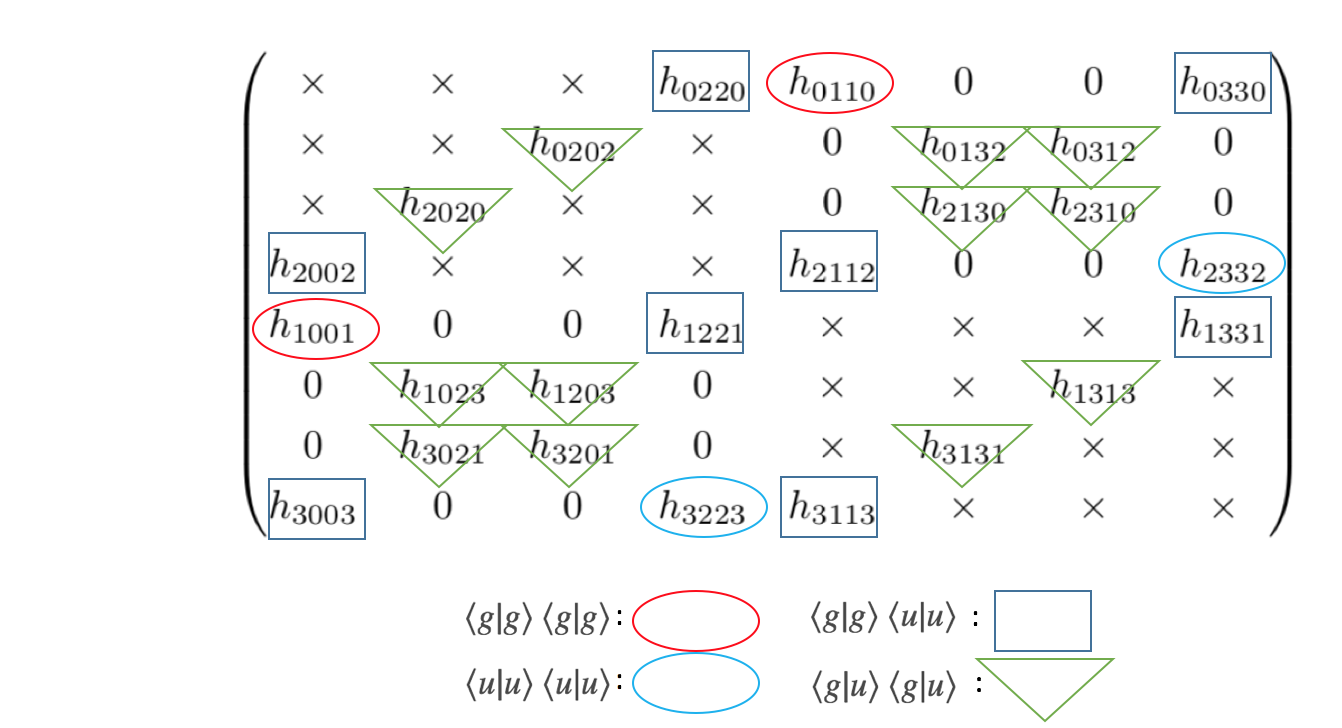
これで論文のTable Ⅲを再現出来た。
2体項Hamiltonianを露わに書くと、次のようになる。先の係数は行列の対角線に関して対称で、生成消滅演算子に関しても$c_p^{\dagger} c_q^{\dagger} c_r c_s$と$c_q^{\dagger} c_p^{\dagger} c_s c_r$は等価({$c_p^{\dagger},c_q^{\dagger}$}$=0$, {$c_p,c_q$}$=0$, {$c_p^{\dagger},c_q$}$=\delta_{p,q}$)なので、右上半分だけについて表記する。2倍することになるが、これは前の$\frac{1}{2}$と打ち消しあう。
\begin{eqnarray}
\mathcal{H}^{(2)} &=& \frac{1}{2} \sum_{p,q,r,s} h_{pqrs} c^{\dagger}_p c^{\dagger}_q c_r c_s \\
&=& h_{0110} \, c_0^{\dagger} c_1^{\dagger} c_1 c_0 +
h_{2332} \, c_2^{\dagger} c_3^{\dagger} c_3 c_2 +
h_{0330} \, c_0^{\dagger} c_3^{\dagger} c_3 c_0 +
h_{1221} \, c_1^{\dagger} c_2^{\dagger} c_2 c_1 \\
&+&
h_{0220} \, c_0^{\dagger} c_2^{\dagger} c_2 c_0 +
h_{0202} \, c_0^{\dagger} c_2^{\dagger} c_0 c_2 +
h_{1331} \, c_1^{\dagger} c_3^{\dagger} c_3 c_1 +
h_{1313} \, c_1^{\dagger} c_3^{\dagger} c_1 c_3 \\
&+&
h_{0132} \, c_0^{\dagger} c_1^{\dagger} c_3 c_2 +
h_{2310} \, c_2^{\dagger} c_3^{\dagger} c_1 c_0 +
h_{0312} \, c_0^{\dagger} c_3^{\dagger} c_1 c_2 +
h_{2130} \, c_2^{\dagger} c_1^{\dagger} c_3 c_0 \\
\\
&=& h_{0110} \, c_0^{\dagger} c_1^{\dagger} c_1 c_0 +
h_{2332} \, c_2^{\dagger} c_3^{\dagger} c_3 c_2 +
h_{0330} \, c_0^{\dagger} c_3^{\dagger} c_3 c_0 +
h_{1221} \, c_1^{\dagger} c_2^{\dagger} c_2 c_1 \\
&+&
(h_{0220}-h_{0202}) \, c_0^{\dagger} c_2^{\dagger} c_2 c_0 +
(h_{1331}-h_{1313}) \, c_1^{\dagger} c_3^{\dagger} c_3 c_1 \\
&+&
h_{0132} \, (c_0^{\dagger} c_1^{\dagger} c_3 c_2 + c_2^{\dagger} c_3^{\dagger} c_1 c_0) +
h_{0312} \, (c_0^{\dagger} c_3^{\dagger} c_1 c_2 + c_2^{\dagger} c_1^{\dagger} c_3 c_0) \\
\end{eqnarray}
これで論文中の式(67)を再現出来た。
まとめ
1.原子軌道$\psi(r)$の線形結合で分子軌道$\phi (r)$を構成する。
\begin{eqnarray}
\phi_g (r) &=& c_{11} \psi_1(r) + c_{12} \psi_2(r) \\
\phi_u (r) &=& c_{21} \psi_1(r) + c_{22} \psi_2(r) \\
\end{eqnarray}
2.原子軌道間の積分値$h_{pq}^{'}, h_{pqrs}^{'}$をPyQuanteで数値計算。
\begin{eqnarray}
h^{'}_{pq} &=& \int \psi^{*}_p({\bf r}) \left( -\frac{\nabla^2_{{\bf r}}}{2} - \sum_{i} \frac{Z_i}{|R_i-{\bf r}|} \right) \psi_q({\bf r}) \, d{\bf r} \\
h^{'}_{pqrs} &=& \iint \psi^{*}_p({\bf r_1}) \psi^{*}_q({\bf r_2}) \frac{1}{|{\bf r_1}-{\bf r_2}|} \psi_r({\bf r_2}) \psi_s({\bf r_1}) \, d{\bf r_1} d{\bf r_2} \\
\end{eqnarray}
3.分子軌道間の積分値$h_{pq}, h_{pqrs}$を、原子軌道間の積分値$h_{pq}^{'}, h_{pqrs}^{'}$の足し合わせで計算。
\begin{eqnarray}
h_{gg} &=& \int d{\bf r} \, \phi^{*}_g({\bf r}) \left( -\frac{\nabla^2_{{\bf r}}}{2} - \sum_{i} \frac{Z_i}{|R_i-{\bf r}|} \right) \phi_g({\bf r})\\
&=& \int d{\bf r} \, \left( \psi^{*}_1({\bf r}) + \psi^{*}_2({\bf r}) \right) U_1({\bf r}) \left( \psi_1({\bf r}) + \psi_2({\bf r}) \right) \\
&=& \int \psi^{*}_1({\bf r}) U_1({\bf r})\psi_1({\bf r}) d{\bf r} + \int \psi^{*}_1({\bf r}) U_1({\bf r})\psi_2({\bf r}) d{\bf r} + \int \psi^{*}_2({\bf r}) U_1({\bf r})\psi_1({\bf r}) d{\bf r} + \int \psi^{*}_2({\bf r}) U_1({\bf r})\psi_2({\bf r}) d{\bf r} \\
&=& h^{'}_{11} + h^{'}_{12} + h^{'}_{21} + h^{'}_{22} \\
\\
h_{gggg} &=& \braket{g}{g} \braket{g}{g} \\
&=& (\bra{1}+\bra{2}) (\ket{1}+\ket{2}) \, (\bra{1}+\bra{2}) (\ket{1}+\ket{2}) \\
&=& h^{'}_{1111} + 4 h^{'}_{2111} + 4h^{'}_{2121} + 2h^{'}_{2211} + 4h^{'}_{2221} + h^{'}_{2222}
\end{eqnarray}
多原子、多電子の場合でも同様に数値計算出来る。(最後まで一気通貫でやってくれる計算ソフトあったら教えてください。。。)