はじめに
統計の教科書を読んでいるとよく出てくる主成分分析ですが、どんなところで使えばいいのかわからないのでいくつかのデータで試してみました。
私の体感ですが、統計と工学の分野で使われ方に差があると思います。
統計の分野では、3次元以上の多次元データを次元縮約して可視化する・新しい軸の解釈をする、多次元データを次元縮約してクラスタリングや機械学習の前処理に使う、重回帰分析のときに独立変数間の相関をなくす(多重共線性の解消)などです。
工学の分野(流体力学)では、例えばカルマン渦をハイスピードカメラで撮影して、その画像たちに対して主成分分析を行い、寄与率の高いモードを抜き出すことで物理現象の理解に役立てることなどに使われています。低ランク近似とも言います。
これは固有直交分解(Proper Orthogonal Decomposition, POD)と呼ばれていますが、主成分分析と同じです。
参考
主成分分析がわかりやすく解析されています。
Qiita 意味がわかる主成分分析
導出がまとめられています。この投稿では使い方のみに絞ります。
Qiita 主成分分析について
7科目のテストの点数を次元縮約して、どんな生徒なのか考えます。
主成分分析 - 統計科学研究所
アヤメのデータで次元縮約してクラスタリングします。
Qiita scikit-learnを使用した主成分分析(PCA)
カルマン渦の可視化画像に固有直交分解している例です。
平邦彦, "固有直交分解による流体解析:1.基礎", ながれ, Vol.30, 2011, pp.115-123
主成分分析
主成分分析は、データを軸(基底)に射影したときに分散が最も大きくなるような軸を探してくる操作です。
その目的はデータの分散共分散行列を固有値分解して、データに固有ベクトルをかけることで達成できます。
軸の直交性は保ったまま変換する直交基底変換です。
フーリエ変換なんかと同じですね。
使用するモジュール
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.datasets import load_iris #あやめデータセット用
from tensorflow import keras #MINIST用
解析の流れ
- 平均を0にする
- 標準偏差を1にする(しないときもあります)
- 分散共分散行列を計算する
- 分散共分散行列を固有値分解する
- 固有値の大きさ順に並び替える
- データに固有ベクトルをかけて基底変換する
ここまでがどれも共通してやることです。目的に合わせて追加の操作もあります。
軸の解釈を行う場合は、元のデータと基底変換後のデータの相関を表す因子負荷量を計算します。新たしい軸が元の軸とどんな対応関係にあるかがわかります。
次元の縮約や低ランク近似で、いくつの次元を選べばいいか判断する定量的な指標として、固有値の合計に占めるn番目までの固有値の累積和を計算する累積寄与率があります。
これをもとに何次元落とすか決めます。
データを$X$とします。上の流れを式でも書きます。
cov = {\rm COV}(X) \\
UWU^T = {\rm SVD}(cov) \\
{\bar X} = XU
$\bar X$は直交基底変換後のデータです。
$\bar X$と元のデータ$X$の相関を示す指標に因子負荷量がります。
固有値の平方根と固有ベクトルの積で求まります。
$${\sqrt W} U$$
実例
1. 多変量正規分布
手順を学ぶために多変量正規分布に主成分分析を行います。
np.random.seed(0)
mean = np.array([3.0, 5.0])
cov = np.array([[1.5, 2.0], [2.0, 4.0]])
data = np.random.multivariate_normal(mean, cov, size=100)
data = data - np.mean(data,axis=0) #各次元の平均を0にする
data /= np.std(data,axis=0)
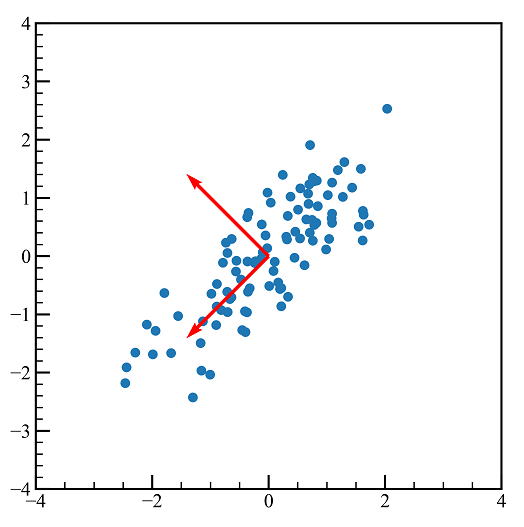
先に平均と標準偏差を操作してしまいましたが、これが元のデータです。
cov = np.cov(data, rowvar=False) #分散共分散行列
u,w,_ = np.linalg.svd(cov) #固有値分解
pca_data = data.dot(u)
pca_ax = u.dot(u) #赤矢印
fig,axes = plt.subplots(figsize=(6,8))
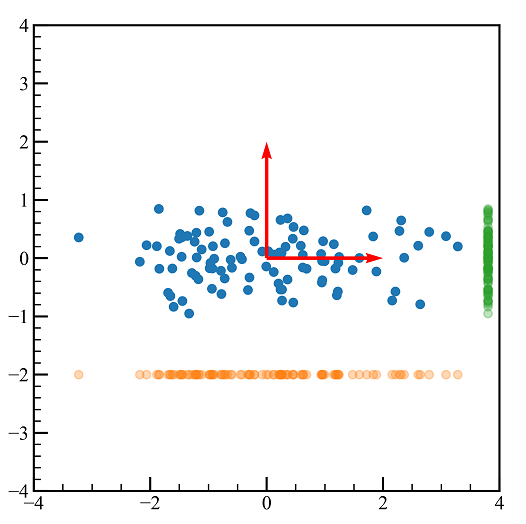
axes.scatter(pca_data.T[0],pca_data.T[1]) #元データ回転
axes.scatter(pca_data[:,0].T,-2.0*np.ones(pca_data.shape[0]),alpha=0.3) #PC1射影
axes.scatter(3.8*np.ones(pca_all.shape[0]),pca_data[:,1].T,alpha=0.3)
axes.set_aspect("equal")
axes.set_ylim(-4.0,4.0)
axes.set_xlim(-4.0,4.0)
axes.quiver(0,0,pca_ax[0,0],pca_ax[0,1],color = "red",angles = "xy", scale_units = "xy",scale = 0.5)
axes.quiver(0,0,pca_ax[1,0],pca_ax[1,1],color = "red",angles = "xy", scale_units = "xy",scale = 0.5)
上の図の赤矢印は$U$をプロットしたものです。
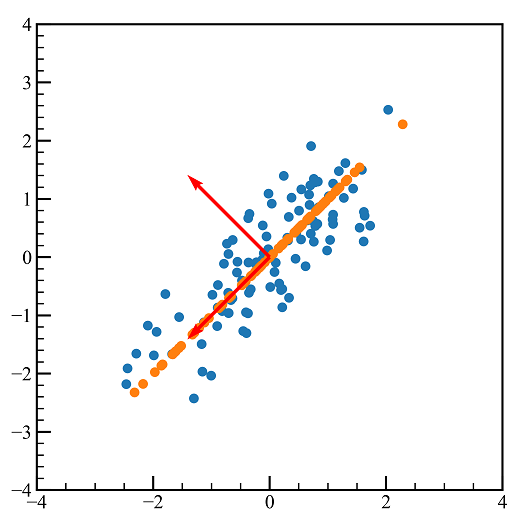
モード分解はこのように次元を落として逆変換します。
フーリエ変換して、周波数空間でフィルタをかけて、逆フーリエ変換してもとに戻すのと同じ感じです。
pca_approx = np.copy(pca_data)
pca_approx[:,1:] = 0.0 #低ランク近似
recon = pca_approx.dot(u.T) #逆変換
fig,axes = plt.subplots(figsize=(6,8))
axes.scatter(data.T[0],data.T[1])
axes.scatter(recon.T[0],recon.T[1])
axes.quiver(0,0,u[0,0],u[0,1],color = "red",angles = "xy", scale_units = "xy",scale = 0.5)
axes.quiver(0,0,u[1,0],u[1,1],color = "red",angles = "xy", scale_units = "xy",scale = 0.5)
axes.set_aspect("equal")
axes.set_ylim(-4.0,4.0)
axes.set_xlim(-4.0,4.0)
累積寄与率も見ます。
次元の縮約をするときに、いくつの次元を残せばだいたいデータを説明できるかを定量的に知るための指標です。
np.sum(w[0])/np.sum(w)
>>> 0.9080218762749276
2. 次元の縮約 テストの点数
統計科学研究所のテストデータを使用します。9科目166人分のデータです。
9次元あるので、生徒がどんな傾向にあるのか判断するのが難しいです。
そこで2次元まで落として、軸を解釈して生徒の傾向を掴みます。
統計科学研究所 統計データ
2-1. データの読み込み
csv_data = pd.read_csv("seiseki.csv")
csv_data
>>>
kokugo shakai sugaku rika ongaku bijutu taiiku gika eigo
0 30 43 51 63 60 66 37 44 20
1 39 21 49 56 70 72 56 63 16
2 29 30 23 57 69 76 33 54 6
3 95 87 77 100 77 82 78 96 87
4 70 71 78 67 72 82 46 63 44
... ... ... ... ... ... ... ... ... ...
161 82 78 80 88 80 69 83 78 90
162 0 8 2 9 5 18 42 2 1
163 45 26 29 24 31 57 68 40 27
164 73 31 43 32 59 64 82 48 56
165 60 85 89 80 56 79 81 45 85
166 rows × 9 columns
2-2. 散布図行列・相関行列
データをいきなり主成分分析にかけてしまう前に、散布図行列を見てどんなデータなのか確認します。
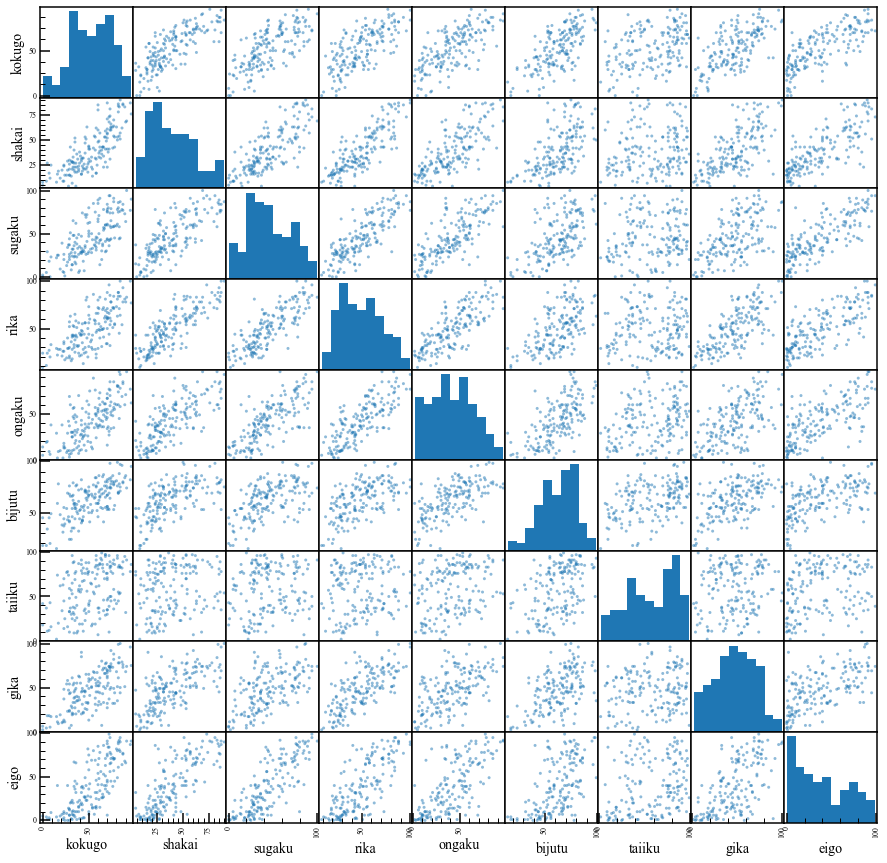
pd.plotting.scatter_matrix(csv_data, figsize=(15, 15))
正直これを見ただけでも主成分分析の結果がだいたいどうなるかわかってしまいますね。
国語、社会、理科、音楽、美術、技術家庭科、英語はそこそこ相関があります。
体育だけ他の教科と相関が低いです。
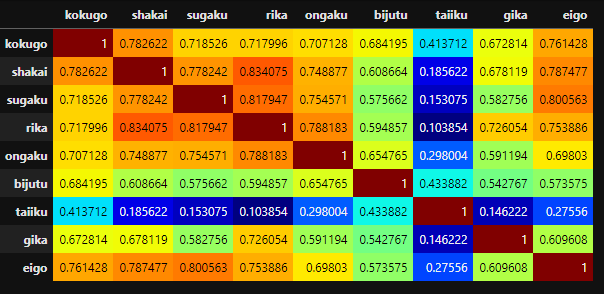
相関行列も見ます。
csv_data.corr().style.background_gradient(axis=None, cmap="jet")
2-3. 主成分分析
主成分分析を行います。
col = csv_data.columns #列名
data = csv_data.to_numpy().astype("float64")
data -= np.mean(data,axis=0) #各列の平均を0にする
data /= np.std(data,axis=0) #各列を標準偏差で正規化
cov = np.cov(data, rowvar=False) #分散共分散行列
u,w,_ = np.linalg.svd(cov) #固有値分解 u:固有値ベクトル w:固有値
sum_w = np.sum(w)
cr = []
for w_ in w:
cr.append(w_/sum_w)
ccr = np.cumsum(cr) #累積寄与率
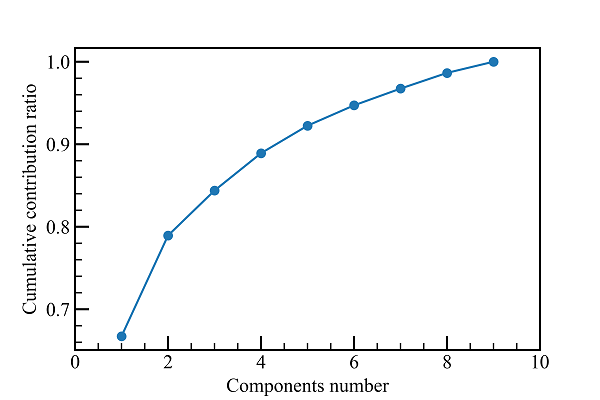
まずは累積寄与率を見ます。
fig,axes = plt.subplots()
axes.plot(list(range(1,len(ccr)+1)),ccr,marker="o")
axes.set_xlabel("Components number")
axes.set_ylabel("Cumulative contribution ratio")
axes.set_xlim(0,10)
2次元まで落としても、80%くらいの情報は残っているようです。
主成分得点を見ます。
pca = data.dot(u)
fig,axes = plt.subplots(figsize=(6,8))
axes.scatter(pca.T[0],pca.T[1])
axes.set_aspect("equal")
axes.set_xlim(-6.0,6.0)
axes.set_ylim(-6.0,6.0)
axes.set_xlabel("PC1")
axes.set_ylabel("PC2")
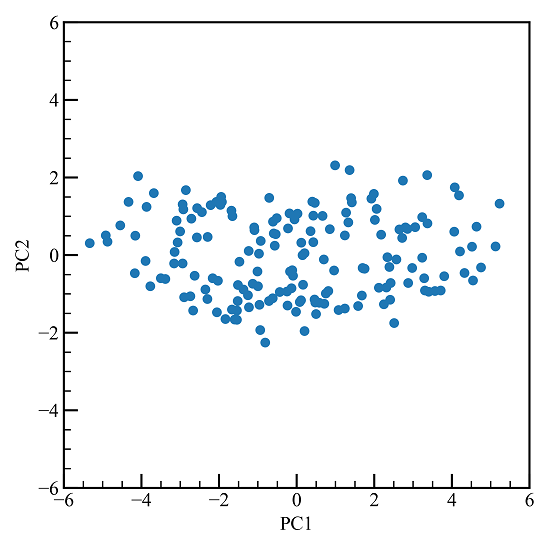
9次元のデータが2次元になりました。しかし、PC1とPC2の意味がわかりません。
そこで元のデータと変換後のデータの相関を表す因子負荷量を計算します。
fl = np.sqrt(w) * u
# FC1
fig,axes = plt.subplots()
axes.scatter(list(range(fl.shape[0])),fl[:,0])
plt.xticks(list(range(fl.shape[0])),list(col))
axes.set_ylabel("FC1")
plt.xticks(rotation = 20)
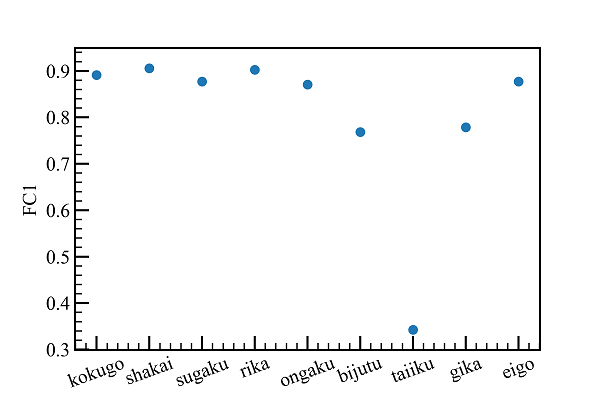
第一主成分軸と関係が深い教科の値が大きくでます。
体育以外の教科と関連が深いようです。
# FC2
fig,axes = plt.subplots()
axes.scatter(list(range(fl.shape[0])),fl[:,1])
plt.xticks(list(range(fl.shape[0])),list(col))
plt.xticks(rotation = 20)
axes.set_ylabel("FC2")
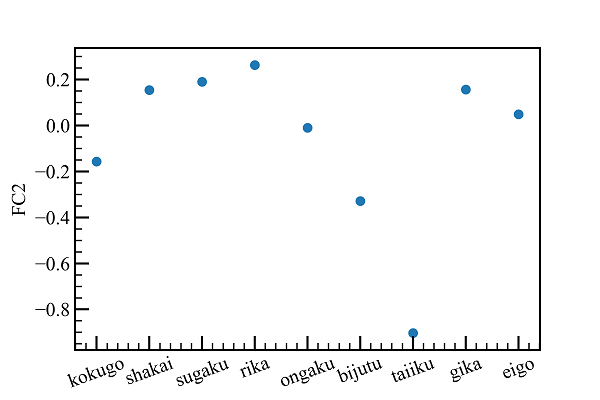
符号は反転ですが、値の絶対値の大きさに意味があります。
第二主成分軸は体育が強く関係します。
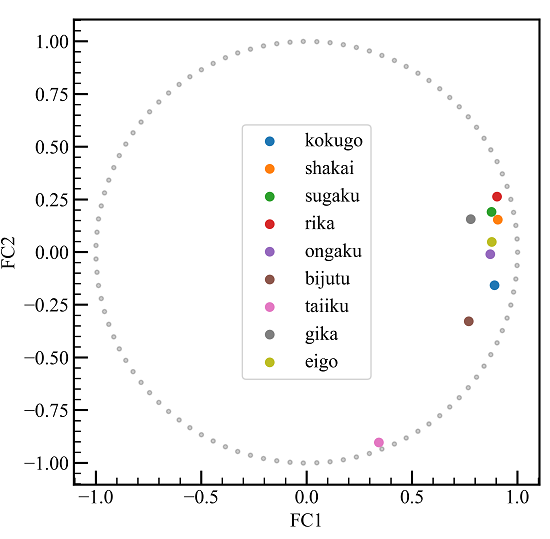
同時にプロットしてもわかりやすいです。
def circle(n,r=1):
"""
円を描く nは分割数
"""
rad = np.linspace(0.0,2.0*np.pi,n)[1:] #0と2piが重ならないように
return np.cos(rad),np.sin(rad)
c = circle(100)
fig,axes = plt.subplots(figsize=(6,8))
axes.scatter(c[0],c[1],marker=".",color="k",alpha=0.2) #円の描画
for i in range(u.shape[0]):
axes.scatter(fl[i,0],fl[i,1],label=col[i])
axes.set_aspect("equal")
axes.legend(loc="best")
axes.set_xlabel("FC1")
axes.set_ylabel("FC2")
体育以外の科目は第一主成分軸と関係が深い一方、第二主成分軸にはあまり寄与しないようです。
体育はその反対です。
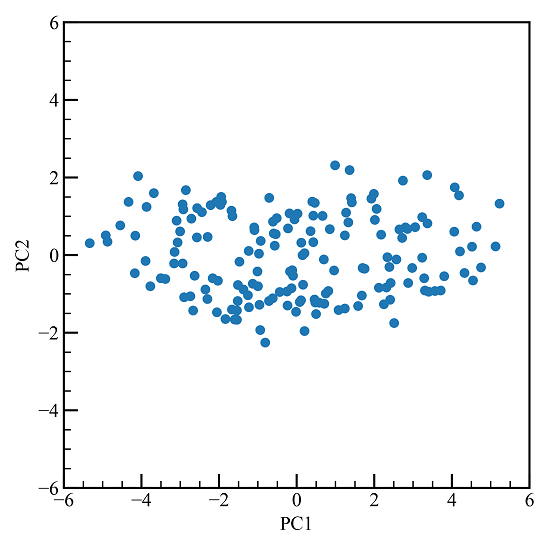
ここでもう一度主成分得点のプロットを見ます。
右に行くほど筆記試験(体育以外)の得点が高く、下に行くほど体育が得意な生徒ということになります。
このように次元を縮約して、新しい軸に意味付けすることでデータを解釈しやすくなります。
3. クラスタリング あやめのデータ
次は3種類(セトサ種, バージカラー種, バージニカ種)のあやめの4つの特徴(ガクの長さ, ガクの幅, 花弁の長さ, 花弁の幅)を記録したデータでクラスタリングを行います。
3-1. データの読み込み
データはsklearnから持ってきます。
iris = load_iris()
iris.keys()
>>> dict_keys(['data', 'target', 'target_names', 'DESCR', 'feature_names', 'filename'])
iris["target_names"]
>>> array(['setosa', 'versicolor', 'virginica'], dtype='<U10')
iris["feature_names"]
>>> ['sepal length (cm)',
'sepal width (cm)',
'petal length (cm)',
'petal width (cm)']
iris_df = pd.DataFrame(iris["data"],columns=iris["feature_names"])
iris_df
>>>
sepal length (cm) sepal width (cm) petal length (cm) petal width (cm)
0 5.1 3.5 1.4 0.2
1 4.9 3.0 1.4 0.2
2 4.7 3.2 1.3 0.2
3 4.6 3.1 1.5 0.2
4 5.0 3.6 1.4 0.2
... ... ... ... ...
145 6.7 3.0 5.2 2.3
146 6.3 2.5 5.0 1.9
147 6.5 3.0 5.2 2.0
148 6.2 3.4 5.4 2.3
149 5.9 3.0 5.1 1.8
150 rows × 4 columns
3-2. 散布図行列・相関行列
ここでも散布図行列と相関行列を見ます。
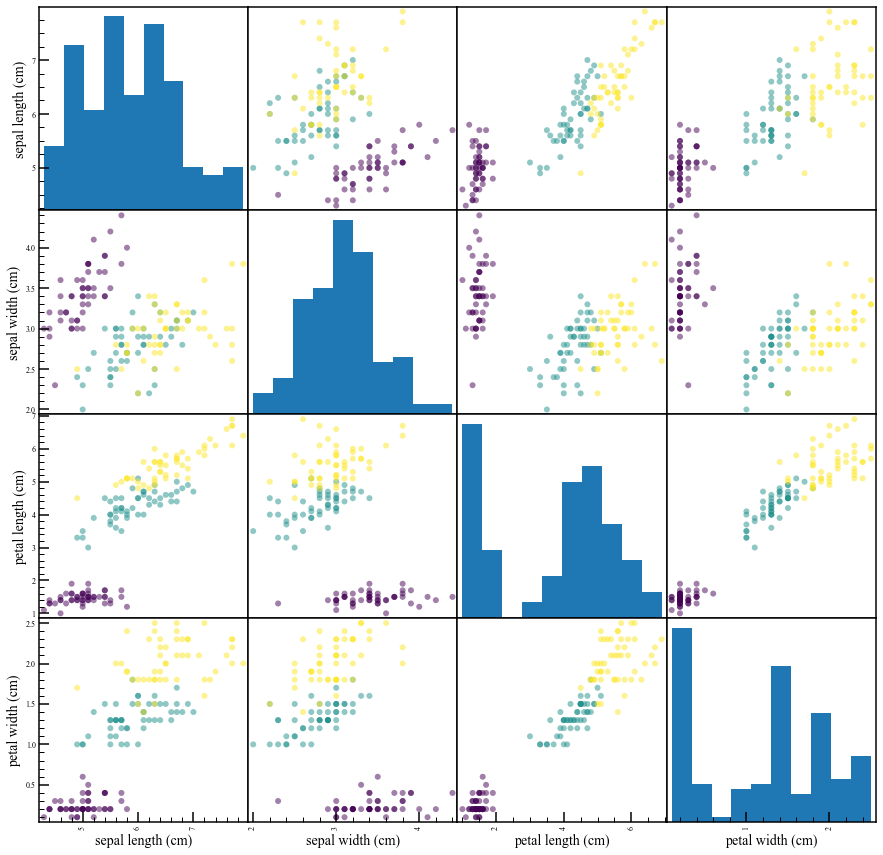
pd.plotting.scatter_matrix(iris_df, figsize=(15, 15),c=iris["target"],marker="o")
なんとなく種ごとにプロットがかたまっていますね。
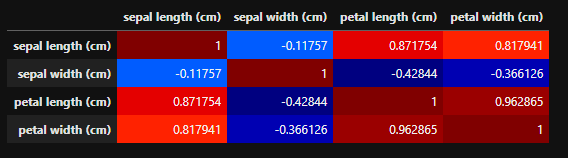
iris_df.corr().style.background_gradient(axis=None, cmap="jet")
3-3. 主成分分析
データを正規化して主成分分析をやっていきます。
data = iris["data"]
data -= np.mean(data,axis=0) #各列の平均を0にする
data /= np.std(data,axis=0) #各列を標準偏差で正規化
cov = np.cov(data, rowvar=False) #分散共分散行列
u,w,_ = np.linalg.svd(cov) #固有値分解 u:固有値ベクトル w:固有値
sum_w = np.sum(w)
cr = []
for w_ in w:
cr.append(w_/sum_w)
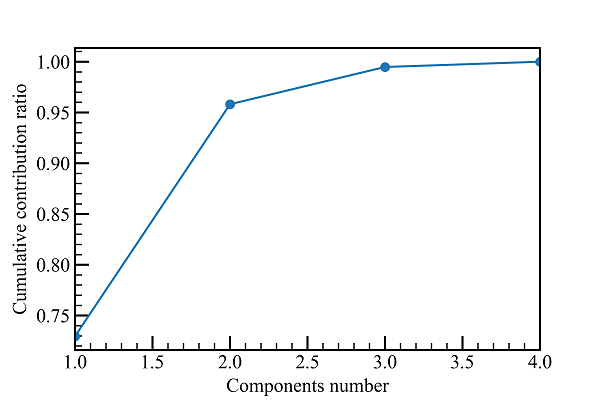
ccr = np.cumsum(cr) #累積寄与率
fl = np.sqrt(w) * u #因子負荷量
グラフの描画は先程と同様なので省略します。
累積寄与率を見ると、2次元だけで95%以上の情報が表現できます。
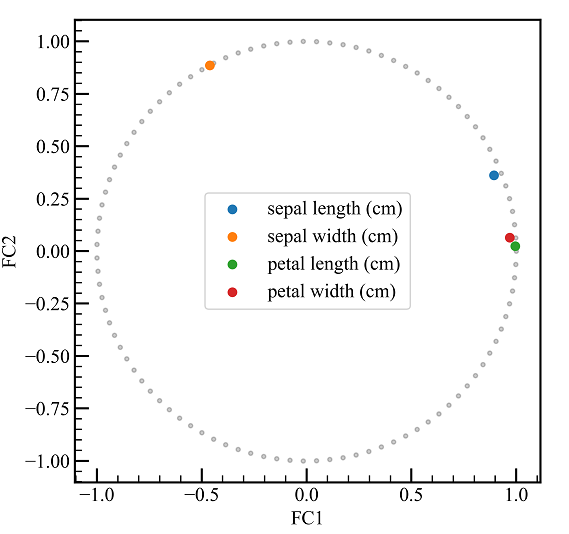
因子負荷量を見ます。
sepal length(ガクの長さ)とpetal length(花弁の長さ), petal width(ガクの幅)は第一主成分軸に強い相関があります。
sepal width(ガクの幅)は第二主成分軸と強い相関があります。
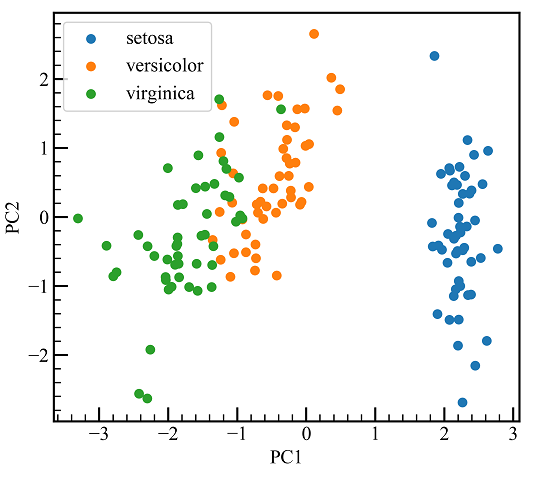
4次元を2次元に落としました。種別にまとまっています。
今回は答えがわかっている状態ですが、種のデータがなく特徴だけのデータでも、k平均法なり線形判別分析なんなりでクラスタリングができます。
4. モード抽出・低ランク近似 MINIST
今度は手書き文字データ(MINIST)の数字の「3」についてモード抽出を行います。
MINISTは28x28のデータなので784次元のデータと見なせます。
これを例えば2次元などに落として逆変換することで、特徴的なモードを見ることができます。
4-1. データの読み込み
kerasからデータを持ってきます。
mnist = keras.datasets.mnist
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()
num_3 = train_images[train_labels==3][0:1000] #3だけ
flatten_imgs = num_3.reshape(1000,28*28) #28x28の画像を1次元配列にする
4-2. 主成分分析 モード抽出・低ランク近似
flatten_imgs = flatten_imgs - np.mean(flatten_imgs,axis=0) #各列の平均を0にする
cov = np.cov(flatten_imgs, rowvar=False) #分散共分散行列
u,w,_ = np.linalg.svd(cov) #固有値分解 u:固有値ベクトル w:固有値
sum_w = np.sum(w)
cr = []
for w_ in w:
cr.append(w_/sum_w)
ccr = np.cumsum(cr) #累積寄与率
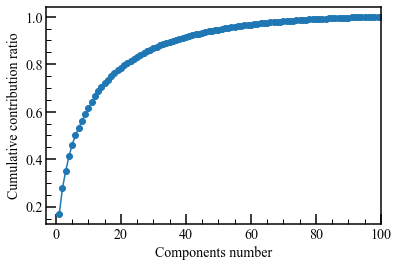
784次元までありますが、100次元までを表示しています。
100次元もあればほぼすべての情報が表現できるようです。
今回は試しに3次元と100次元で近似してみます。
pca = flatten_imgs.dot(u)
rank = 3
pca_approx = np.copy(pca)
pca_approx[:,rank:] = 0.0
rebuilt = pca_approx.dot(u.T)
rebuilt_reshape = rebuilt.reshape(1000,28,28)
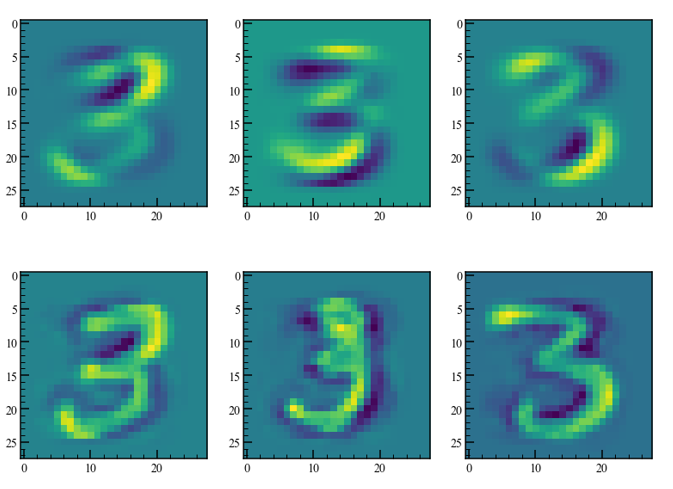
数枚の画像を表示します。
上列がランク3近似、下列がランク100近似です。
ランク3だとデータ間の差が少なく、特徴的なモードのみが残っています。
ランク100だとデータ間の差がはっきりわかり、元のデータがよく再現されています。
まとめ
主成分分析の使いみちを3つ試してみました。
次元の縮約、クラスタリング、モード分解のどれも同じような手順で行うことができます。