今回は主成分分析についての解説記事です。社会人になったので、統計を勉強しています。ブランクがある身にはちょうどいいですね。
イントロ
まずは、実数値データが下図のように散布している状況を考えます。

例えば、これは二次元データですが(x軸を体重、y軸を身長とでも考えてみましょう)次のようにある直線に射影することを考えます。
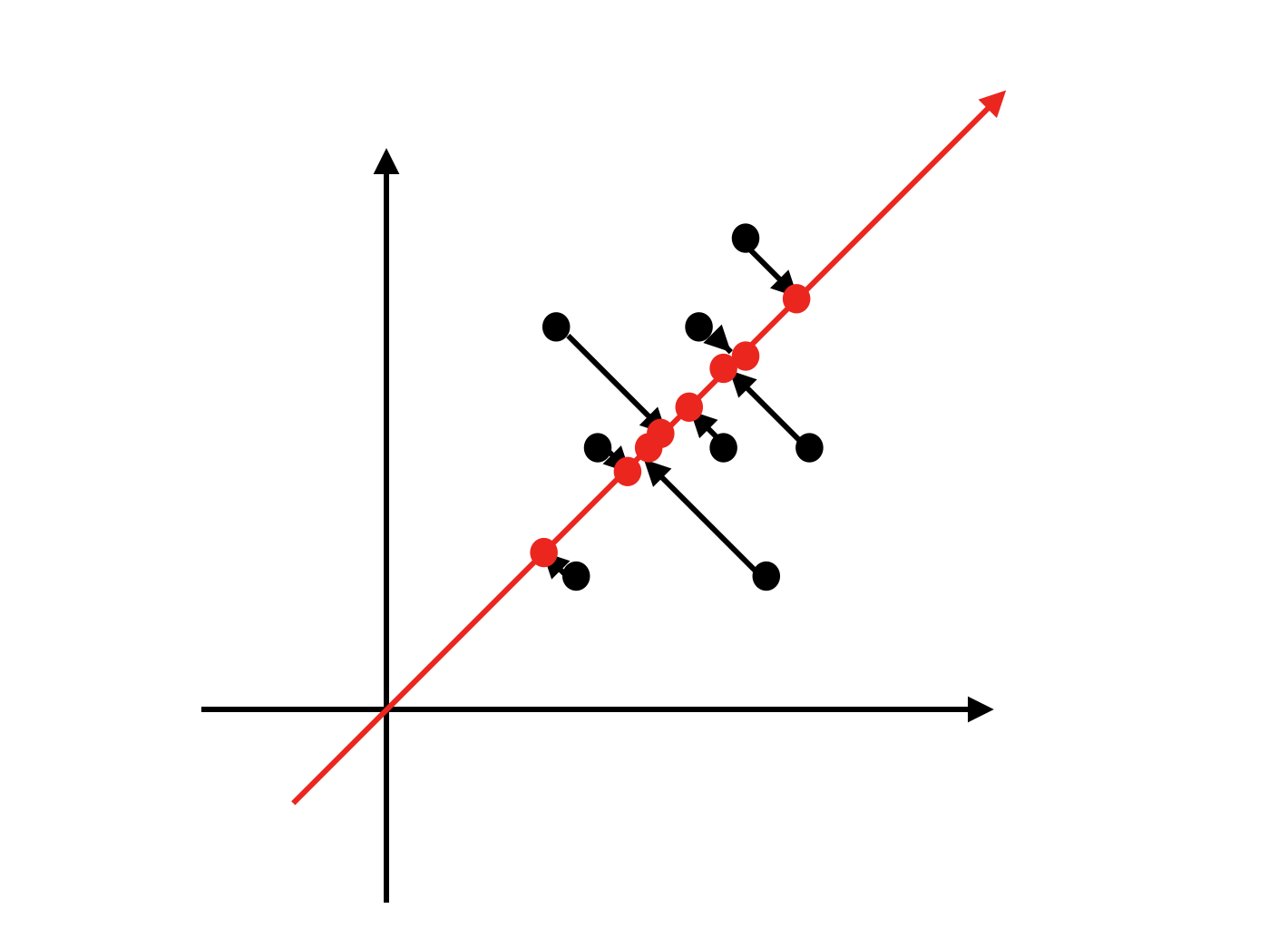
この軸は、解釈次第ですが例えば身体の大きさを表すものだと考えると、それまで2つの指標(体重と身長)で考えていたものを1つの指標で考えられるようになります。うれしい。
射影軸の選び方
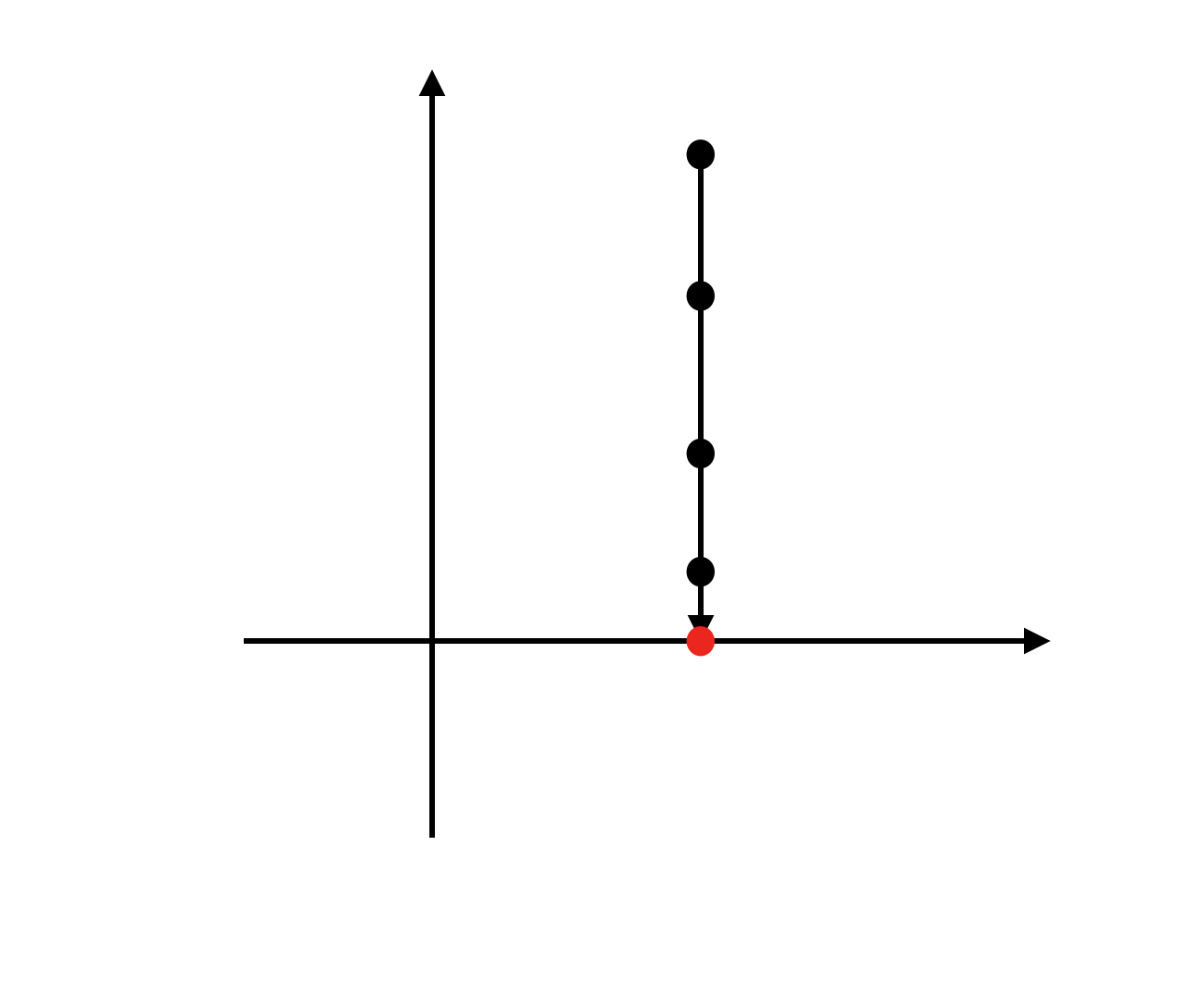
では、次にどんな直線に射影するのが一番いいかを極端な例を交えて考えましょう。次の一直線に並んだデータを考えます。

こうしてしまうと、それぞれのデータの差がなくなってしまいますね。これでは1つの軸で説明できるとしても全く嬉しくありません。つぎに、y軸に射影してみます。

こうすると、x軸のデータは失ってしまいますが(差がないのでそもそも意味がない)、1つの軸で前の情報を保存しつつ説明できていることがわかります。
これらの考察から、データの特徴を失わずに説明する軸を減らすためには、射影したあとのデータが散らばっていればいいということがわかります。散らばり具合ですが、ここでは分散$\sigma^2$という統計量を用いましょう。分散は平均からの差を2乗和したものなので、定量的にデータが散らばっているかがわかります。
$$\sigma^2=\frac{1}{N}\sum_{n=1}^N(x_n-\bar{x})^2$$
ここで、$N$はデータ数、$\bar{x}$はデータの平均です。
問題を言い換えると射影後のデータの分散を最大化する軸を探すということになります。
定式化
データの次元を$P$、データ数を$N$としデータの行列を
X=(x_{i,j})_{i=1,2,\cdots,N,j=1,2,\cdots,P}=
\begin{pmatrix}
x_{11} & \cdots & x_{1P} \\
& \ddots \\
x_{N1} & \cdots & x_{NP}
\end{pmatrix}
とします。また、行ベクトル(各データ)を
$$x_n=(x_{n1},\cdots,x_{nP}), n=1,\cdots,N$$
とします。
ここで、$P$次元のデータのうち、ある成分について他の成分に比べて分散が大きければその方向に大きく依存した軸になってしまうため、ここでは、各成分の平均が0、分散が1となるように正規化しておきます。
すなわち、任意の$p=1,2,\cdots,P$に対して、
$$\frac{1}{N}\sum_{n=1}^N x_{np}=0 , \frac{1}{N}\sum_{n=1}^N(x_{np})^2=1 $$
とします。
射影する軸の単位ベクトルを$w$とします。
各データを軸に射影したときの原点からの長さ$z_n$は以下の図を参考にすれば、$x_n$と$w$の内積を取ればよいことがわかります。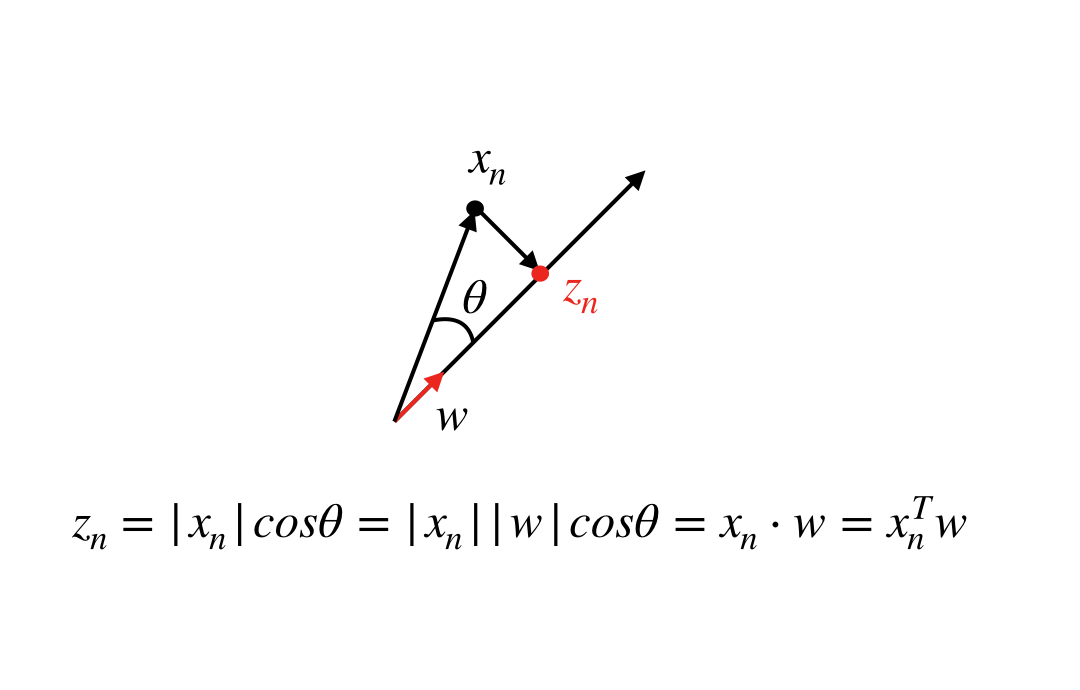
ここで$||$は普通の意味での長さで、$x_n^T$は$x_n$の転置を表します。
すると、射影したデータのそれぞれの長さを表すベクトルは以下で表せます。
z=Xw=
\begin{pmatrix}
z_1 \\
\vdots \\
z_N
\end{pmatrix}
射影した軸に関するデータの平均と分散
$z$の平均と不偏分散を求めましょう。
\begin{align}
\bar{z}&=\frac{1}{N}\sum_{n=1}^{N}z_n \\
&=\frac{1}{N}\sum_{n=1}^{N}x_n \cdot w \\
&=\frac{1}{N}\sum_{n=1}^{N} \sum_{i=1}^{P} x_{ni}w_i \\
&=\sum_{i=1}^{P} w_i(\frac{1}{N}\sum_{n=1}^{N} x_{ni} )=0\\
\end{align}
よって、射影後のデータの平均は0ということがわかりました。
次に分散を求めます。
\begin{align}
\frac{1}{N}\sum_{n=1}^N(z_n-\bar{z})^2&=\frac{1}{N}\sum_{n=1}^N(z_n)^2 \\
&=\frac{1}{N}|Xw|^2 \\
&=\frac{1}{N}(Xw)^T(Xw)\\
&=\frac{1}{N}w^TX^TXw \\
&=w^T(\frac{1}{N}X^TX)w \\
&=w^TVw
\end{align}
よって射影後の不偏分散は$V=\frac{1}{N-1}X^TX$の$w$に対する二次形式で与えられることがわかります。
Vの正体
$V$を計算してみましょう。
\begin{align}
V= \frac{1}{N}X^TX \\
&= \frac{1}{N}\begin{pmatrix}
x_{11} & \cdots & x_{1P} \\
& \ddots \\
x_{N1} & \cdots & x_{NP}
\end{pmatrix}^T
\begin{pmatrix}
x_{11} & \cdots & x_{1P} \\
& \ddots \\
x_{N1} & \cdots & x_{NP}
\end{pmatrix}\\
&= \frac{1}{N}\begin{pmatrix}
x_{11} & \cdots & x_{N1} \\
& \ddots \\
x_{1P} & \cdots & x_{NP}
\end{pmatrix}
\begin{pmatrix}
x_{11} & \cdots & x_{1P} \\
& \ddots \\
x_{N1} & \cdots & x_{NP}
\end{pmatrix}\\
&=\begin{pmatrix}
\frac{1}{N}\sum_{n=1}^N x_{n1}^2 &\frac{1}{N}\sum_{n=1}^N x_{n1}x_{n2} & \cdots & \frac{1}{N}\sum_{n=1}^N x_{n1}x_{nP} \\
\frac{1}{N}\sum_{n=1}^N x_{n2}x_{n1}& \frac{1}{N}\sum_{n=1}^N x_{n2}^2 \\
\vdots & & \ddots \\
\frac{1}{N}\sum_{n=1}^N x_{nP}x_{n1} & \cdots & & \frac{1}{N}\sum_{n=1}^N x_{nP}^2
\end{pmatrix}
\end{align}
これは、分散共分散行列ですね!(今、各成分の平均が0になっていることに注意)
分散共分散行列はデータの散りばり具合やそれぞれの成分の関係を集約したものです。
例えば、対角成分を見れば各成分の分散がわかり、非対角成分(たとえば(1,2)成分)を見ると、成分1と成分2の相関係数がわかります。
線形代数の復習
正方行列$A$が与えられたとき、$A^TA$を$A$のグラム行列と言います。つまり、上の$V$はグラム行列です。ここでは、グラム行列の性質を少し述べておきます。
対称性
グラム行列$W=A^TA$は対称行列です。
$$W^T=(A^TA)^T=A^T(A^T)^T=A^TA=W$$
より明らかです。 よってグラム行列の固有値に対応する固有ベクトルは全て互いに直交します。
半正定値性
グラム行列$W=A^TA$は半正定値行列です。
すなわち、任意のベクトル$x$に対して(もちろんAが作用できる型で)
$$x^TWx=x^T(A^TA)x=x^TA^TAx=(Ax)^T(Ax)=|Ax|^2\geq 0$$
なので明らかです。よって、グラム行列の固有値は全て非負です。
よって、以上からグラム行列は半正定値対称行列で、固有値は全て非負で対応する固有ベクトルは全て互いに直交します。
問題化
さて、本題に戻りましょう。
もともとの目的は、射影後の分散を最大にするような方向$w$を探すことでした。$w$の長さは1にしていたのでこの条件のもとで、次の最適化問題を考えましょう。
条件$w^Tw=1$のもとで
$$\frac{1}{N}\sum_{n=1}^N(z_n)^2=w^TVw$$
を最大化する$w$を求めよ。
等式条件の元での最大化問題なので、ラグランジュの未定乗数法を使って求めてみましょう。
解題
ラグランジュ関数
$$L(w)=w^TVw-\lambda(w^Tw-1)$$
とします。
最大値の候補点を探しましょう。任意に$p=1,\cdots,P$をとります。
\begin{align}
\frac{\partial}{\partial w_p}L(w)&=\frac{\partial}{\partial w_p}(w^TVw-\lambda(w^Tw-1)) \\
&=\frac{\partial}{\partial w_p}(\sum_{i,j=1}^P V_{ij}w_iw_j -\lambda\sum_{i=1}^P w_i^2) \\
&=\sum_{j}V_{pj}w_j+\sum{i}V_{ip}w_i-2\lambda w_p \\
&=2(\sum_{i}V_{pi}w_i -\lambda w_p)=0
\end{align}
とおくと、
$$(Vw)p=\lambda w_p$$
となる。$p$は任意だったので、
$$Vw=\lambda w $$
が得られます。すなわち、$w$の候補としては、$V$の固有ベクトルということですね。
これを、最大化したい関数に代入すると、
\begin{align}
w^tVw=w^t(\lambda w)=\lambda w^Tw=\lambda
\end{align}
でこれの最大値は最大固有値となることがわかりますね。
よって、分散を最大にする射影方向は最大固有値となる固有ベクトルの方向ということになります。
いま、$V$は半正定値なので固有値は非負になることが保証されているので分散が負になることはないことに注意しましょう。
一般化
1つの軸に射影するのではなく2つ、3つと軸を増やしてそれらが成す超平面に射影した方が明らかに情報量が多くなります。よって、これらの軸を順に求める方法を考えます。
$1\leq m\leq P$個目の方向を求めるとします。既に求めた軸とは直交していた方が得られる情報量が多くなるので(直交していなければ相関がある)以下の条件で最大化しましょう。
任意の$1\leq i \leq m-1$に対して、
$$w_i^Tw_m=0,w_m^Tw_m=1$$
これで先ほどのようにラグランジュの未定乗数法を使うと、固有値が大きい順に射影する方向を決めて行けば良いことがわかります。(証明は割愛します。今、Vは対称行列なので異なる固有値に対応する固有ベクトルは互いに直交することに注意します。)
なぜこんな結果になるか
なぜ分散共分散行列の大きい固有値に対応する固有ベクトルの方向に射影すると分散が大きくなるのかを考えます。
まず、射影後の分散は
$$w^TVw=w^TA^TAw=(A^TAw)^Tw$$
で表せます。$A^TAw$と$w$の内積ですね。
すなわち、$A^TAw$を$w$の軸に射影した長さになります。絵で表すと、次のようになります。
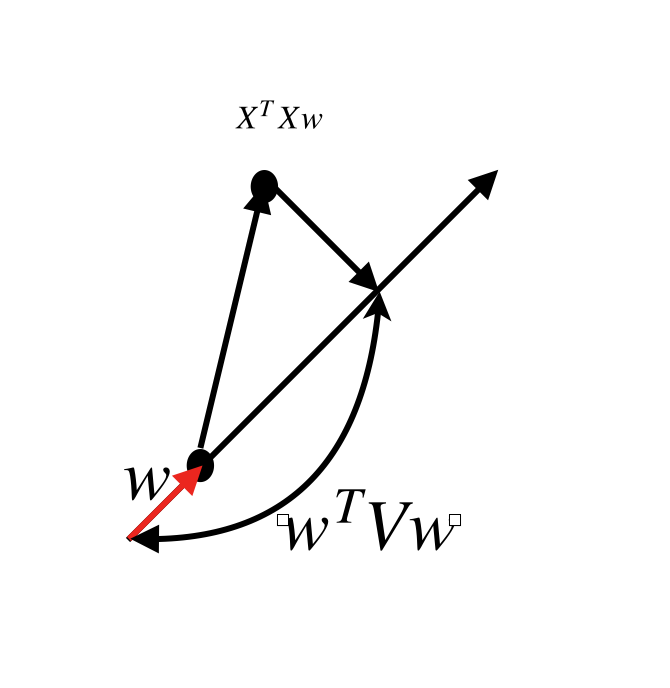
しかし絵の通り$w$が固有ベクトルでない場合は、$w$の軸に射影しなければならないので無駄が生じてしまいます。よって、$X^TX$の固有値が大きい固有ベクトル方向に射影すればいいことがわかります。
この辺りについては、私の記事が参考になると思いますのでよかったら参照してください。
宿題
とはいってもなぜ分散共分散行列が関わってくるのか明確にはよくわかっていません。
グラム行列をもう少し勉強すればわかってくると思うのですが・・・この辺りは自分への宿題です。詳しくわかる有識者の方は教えてくださると嬉しいです。
あとは、プログラムの実装を全くやっていないので、今後やっていきます。