スペクトル分解から行列を理解する

この記事では行列$A$が与えられたときにそれがどんなものなのかを考えていきます。　
というのは、筆者がはじめて高専で行列を学んだときなんだかよくわからなかったからです。　
計算はできるけど、これって一体何を表すんだろう、この数を並べたものは一体なんなんだろうか、とよくわからなかったのです。
大学で数学を学ぶと、自分なりに理解を深めることができたので、ここにシェアします。

前提

固有値・固有ベクトル・対角化および基底などの定義は知っているものと仮定します。

そもそも行列とは

そもそも行列を端的に言い表すとなんでしょうか？

じつは、関数なんですね。自分は20年間生きてきてそんなこともよくわかっていませんでした。

たとえば、$n,m$を自然数として、$A$を$\mathbb{R}^n$から$\mathbb{R}^m$への写像とします。つまり$n$次元のベクトルを$m$次元のベクトルに写す、と。

さらに線形写像といういい性質をもっています。
つまり$\alpha,\beta$を実数¹、$x,y$を$n$次元のベクトルとすると、
$$A(\alpha x+ \beta y )= \alpha A(x)+\beta A(y)$$

がなりたちます。つまりベクトルの線形和を$A$に作用させると、$x,y$にそれぞれ$A$を作用させたものの線形和になるんですね。ここでは関数を意識するために括弧付きでかきましたが、今後は括弧なしで$A(x)$を$Ax$とかきます。また簡単のために今後は$n=m=2$とします。

でもやっぱりよくわからない

行列が線形な関数であるということはわかりましたが、でもそれでもさっぱりわかりません。なにがよくわからないかといえば、たとえば

A=\begin{pmatrix}
1 & 2 \\
3 & 4 
\end{pmatrix}

としたときに、これが一体どんな関数なのかよくわからないということです。
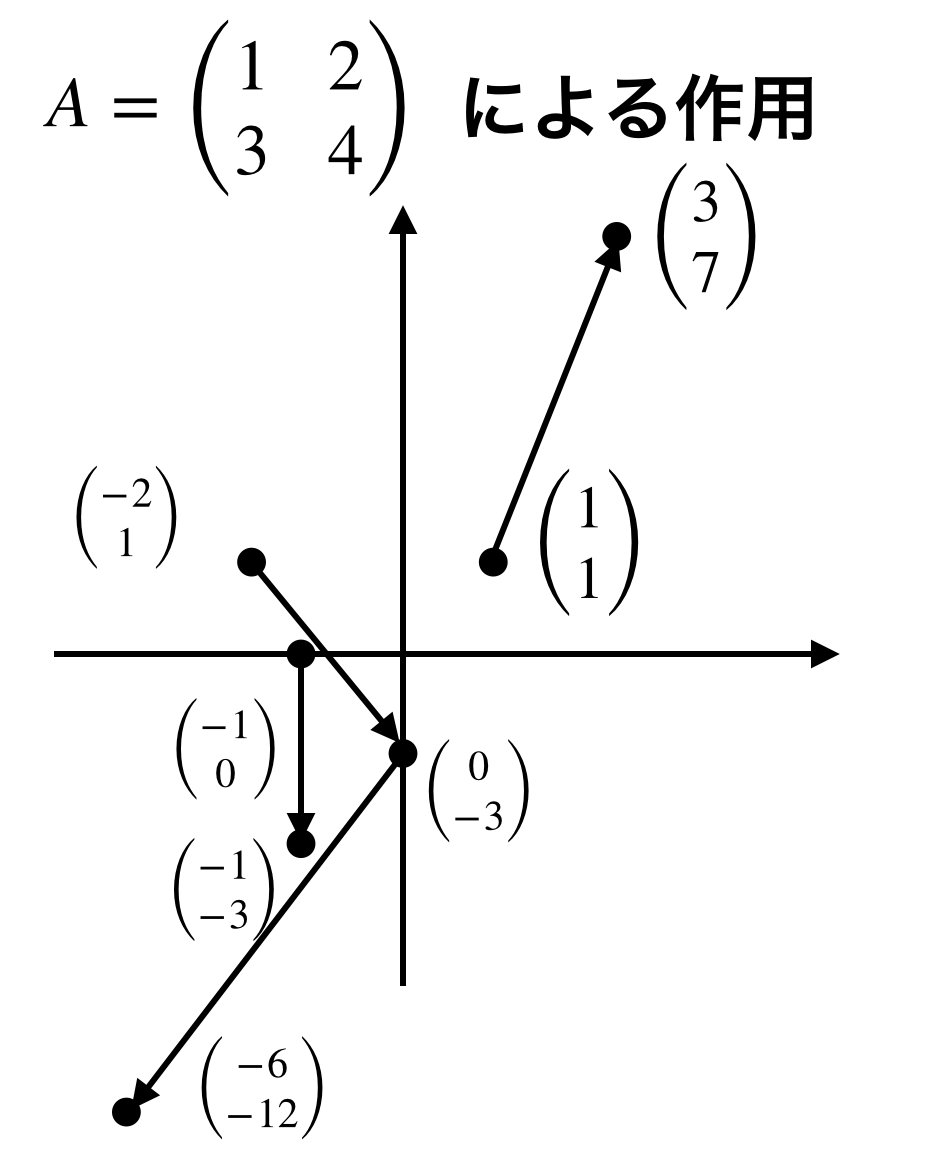
何がわからないか明確にするために色々なベクトルに作用させて実験してみましょう。

$A$をいろんな点に作用させてみた図です。ここから、$A$が一体何者かわかるでしょうか？
正直私には何回も作用させるとどんどん遠方にいくかなぁぐらいしかわかりませんでした。
例えば、$y=x^2$とかだったらすごくわかりやすいですよね。入れた値を$2$乗にして返すよっていうのも理解しやすいですし、$y=x^2$のグラフも視覚的に理解できます。

ここで目標として、$A$の関数としての意味を$y=x^2$レベルまで理解できることとしましょう。

どうやって理解するか

ここでは、数学の常套手段を使います。つまり、なにかよくわからないものを理解するために、理解できるもので構成してやろうってことを考えます。　
例えば、テイラー展開はよくわからない関数をよくわかる多項式で表現してやろうってものです。（ただし無限和）

それでは行列の世界において、よくわかるものはなんでしょうか。

まずは単位行列とゼロ行列

I=\begin{pmatrix}
1 & 0 \\
0 & 1 
\end{pmatrix}, O=\begin{pmatrix}
0 & 0 \\
0 & 0
\end{pmatrix}

が思い浮かぶでしょうね。でもこれだと見通しがわるいです。
なぜなら、単位行列は何もしないという行列をあらわすし、ゼロ行列は全てを$0$に写すというもので、ちょっとこれだけではさすがに$A$をあらわすことはできなさそうです。
それでは次に簡単なものはなんでしょうか。これは色々あるかもしれませんが、　つぎの

\lambda I=\begin{pmatrix}
\lambda & 0 \\
0 & \lambda 
\end{pmatrix}

単位行列に定数倍をかけたものが簡単なのではないでしょうか。　これは、ベクトルを伸ばしたり縮めたりする行列です。まぁこれならよくわかりますよね。

つぎに何をするかというと、どのベクトルを$A$に作用させればその定数倍になるのかを求めます。
果たしてそんなものがあるかは謎ですが、方程式を立ててみます。つまり

$$Ax=\lambda x$$

となるような$x$を求める問題です。ちょっと白々しすぎたかもしれませんが、これは固有値問題ですね！　では次のように右辺を左辺に移行して変形してやりましょう.

$$(A-\lambda I)x=0$$

ここで、今求めたいベクトルは作用させると定数倍になって返ってくるようなベクトルなので、
$0$ベクトルだとあまり嬉しくないですよね。　
よって、上の方程式で$x=0$でないような解を持つための条件を考えます。　これは$(A-\lambda I)$が逆行列をもたないという条件と同値です。　(上の式の左辺に$(A-\lambda I)^{-1}$を左から作用させると, $x=0$がでてくる。) つまりこれは$(A-\lambda I)$の行列式が$0$になるということです。

|A-\lambda I|=\begin{vmatrix}
1-\lambda & 2 \\
3 & 4-\lambda 
\end{vmatrix}
=\lambda^2 -5\lambda-2=0

の解を$\lambda_1, \lambda_2$とします。対応する固有ベクトルを$v_1,v_2$とおきます。すなわち、次が成り立ちます。

$$Av_1=\lambda_1 x_1,Av_2=\lambda_2v_2$$

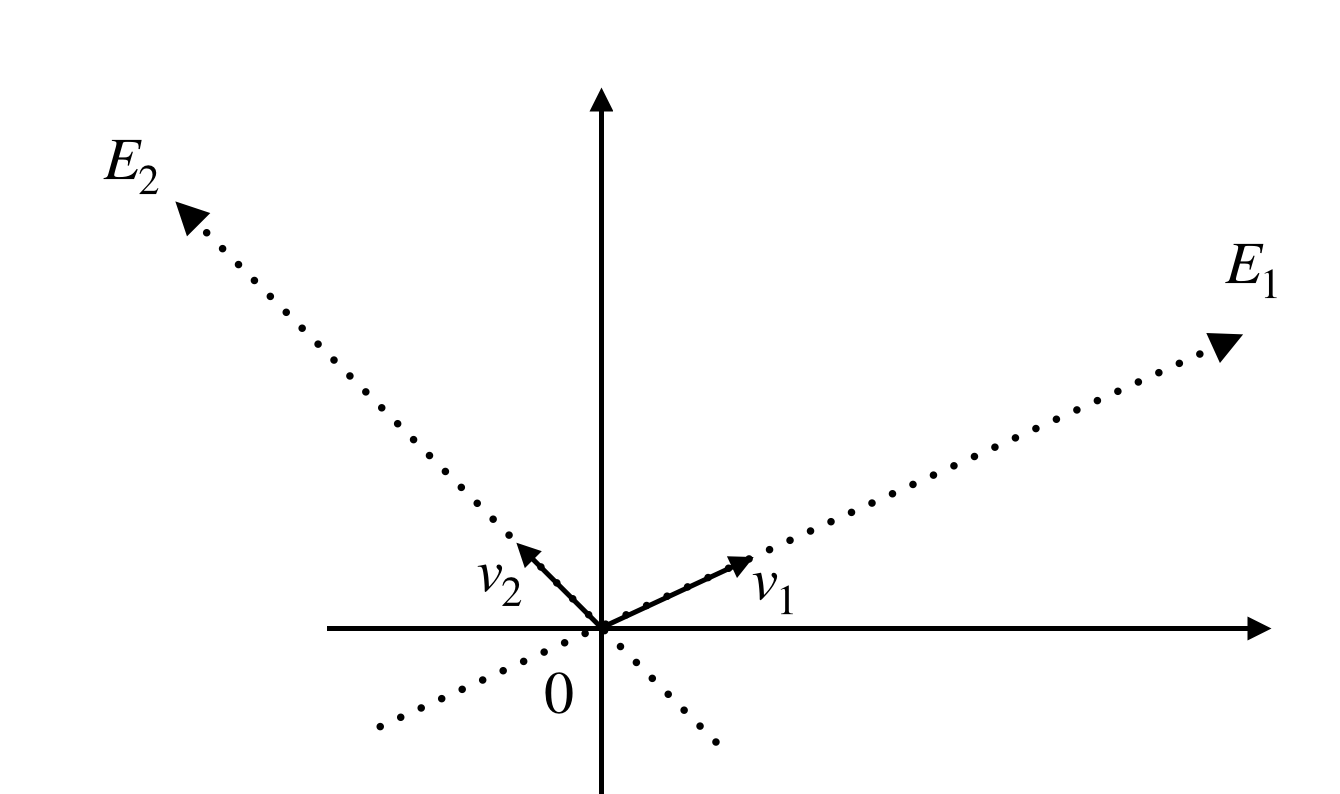
また、固有ベクトルがわかると次の固有空間というものが得られます
$$E_1=\{cv_1:c \in\mathbb{R}\backslash \{0\} \}$$

$$E_2=\{cv_2:c \in\mathbb{R}\backslash \{0\} \}$$

集合がでてきてびっくりするかもしれませんが、そんなに怖くはなくて、固有ベクトルの定数倍全体の集合です。

これを絵で描くと

になります。 ここで、$E_1,E_2$の直線は直交するとは限らないことに注意しましょう。

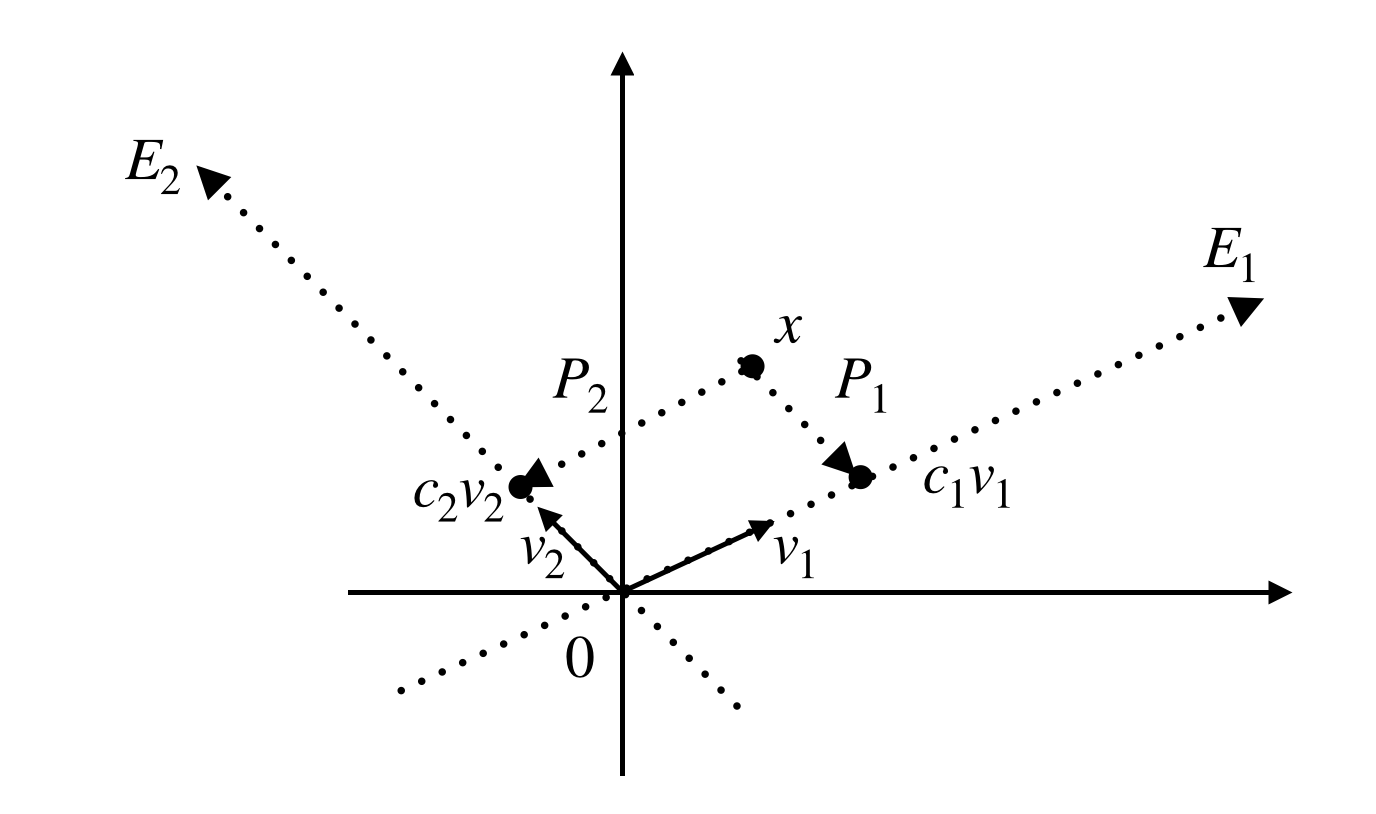
ここで異なる固有値に対応する固有ベクトルは線型独立だということは一般的に知られています。また、いま$\mathbb{R}^2$を考えているので、$\mathbb{R}^2$の任意の元は$v_1,v_2$の線型結合でかけることになります。
つまり任意に$x \in \mathbb{R}^2$をとってくると、$x$に依存したある定数$c_1,c_2$がとれて、

$$x=c_1v_1+c_2v_2$$

とできます。これまた、絵で描くと以下のようになります。

この図からわかるようにこれは、$x$をそれぞれ$E_1,E_2$に射影していることにほかなりません。その作用を$P_1,P_2$と表しました。つまり、

$$P_1x=c_1v_1, P_2x=c_2v_2$$

です。
$P_1P_2=P_2P_1=O$に注意しましょう。これはどういうことかというと、任意のベクトルを$E_1$に射影してから$E_2$に射影すると原点にいくということです。これは逆にしても同じです。絵からも明らかですね。
また、これも明らかですが$P_1P_1=P_1, P_2P_2=P_2$が成り立ちます。簡単にいえば何回射影しても同じということです。

さて、$x=c_1v_1+c_2v_2$に左から$A$を作用させてみましょう。

Ax=A(c_1v_1+c_2v_2)=c_1Av_1+c_2Av_2\\
=c_1\lambda_1v_1+c_2\lambda_2v_2

とかけます。1行目は$A$の線型性、2行目は$v_1,v_2$が$A$の固有ベクトルであることを使いました。固有値と$c_1,c_2$の場所を入れ替えてもう一度書くと、

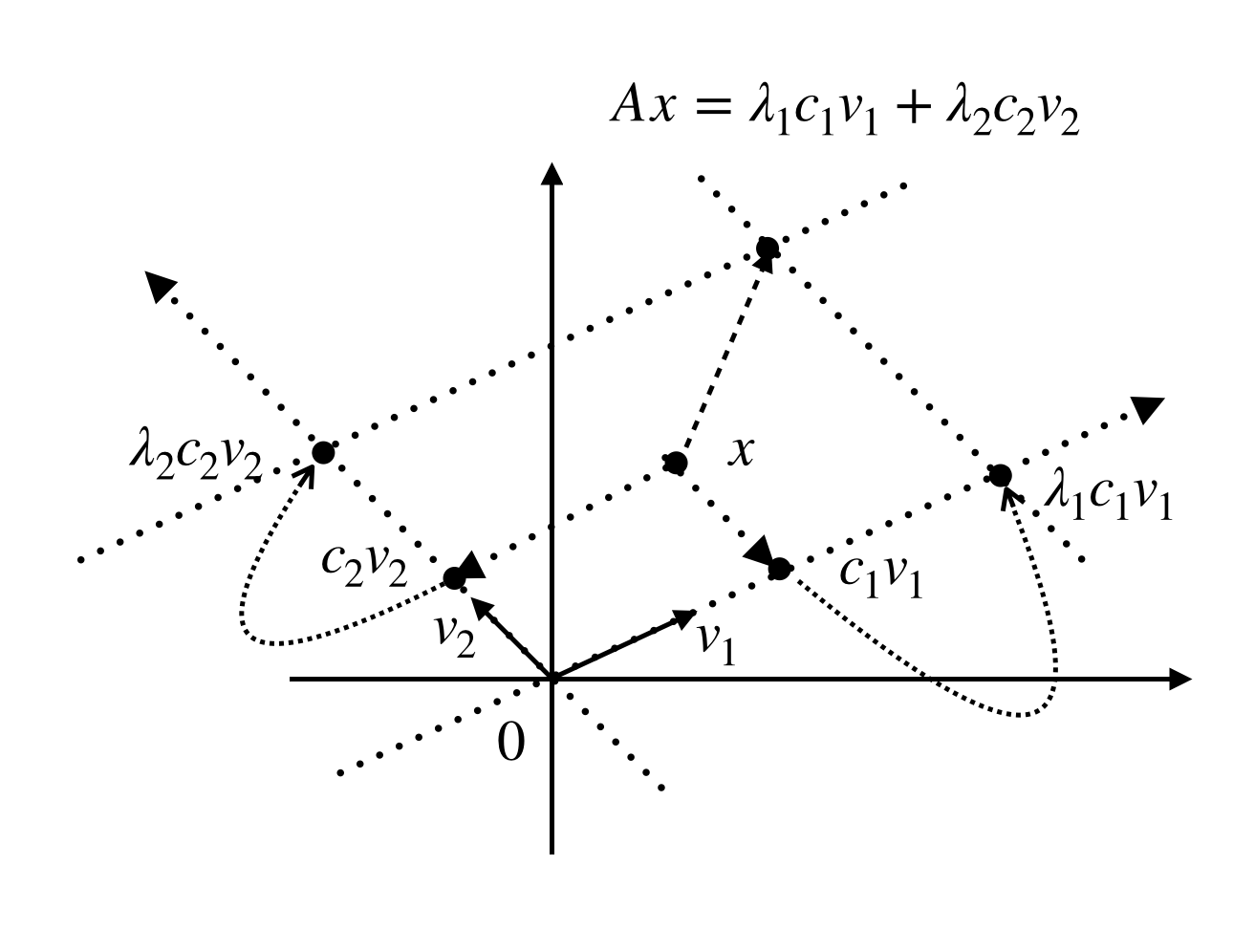
$$Ax=\lambda_1c_1v_1+\lambda_2c_2v_2$$

になります。また射影の言葉でかくと、

$$Ax=\lambda_1c_1v_1+\lambda_2c_2v_2=\lambda_1 P_1x+ \lambda_2P_2x$$

になります。$x$は任意なので、次のようにかいてもいいです。

$$A=\lambda P_1 +\lambda_2 P_2$$

これを行列のスペクトル（射影）分解といいます。
これはどういうことか以下の図であらわすと、

のようになります。もうここまでくると、$A$の行列としての意味は一目瞭然ですね。すなわち、

それぞれの固有空間に射影したものを固有値倍したものを足し合わせたもの

です！

Aのn乗

$A$をここまで理解すれば、$A$の$n$乗を求める計算も楽チンです。

$A^n=(\lambda_1P_1+\lambda_2P_2)^n=\lambda_1^n P_1+\lambda_2^n P_2$

射影の性質をつかいました。

射影行列の求め方

射影を使うと行列がよくわかったけど、でもどうやって射影を求めるの？っていう疑問は出て当然です。ここで対角化を用います。
$A$を対角化すると正則行列$P$が存在して、以下のようにかけますね。

P^{-1}AP=\Gamma=\begin{pmatrix}
\lambda_1 & 0 \\
0 & \lambda_2 
\end{pmatrix}
=\lambda_1 \begin{pmatrix}
1 & 0 \\
0 & 0 
\end{pmatrix} +
\lambda_2 \begin{pmatrix}
0 & 0 \\
0 & 1 
\end{pmatrix}

これを$A$について解いてやると、

A
=\lambda_1 P\begin{pmatrix}
1 & 0 \\
0 & 0 
\end{pmatrix}P^{-1} +
\lambda_2 P\begin{pmatrix}
0 & 0 \\
0 & 1 
\end{pmatrix}P^{-1}
=\lambda_1 P_1 +\lambda_2 P_2

とできます。よって射影行列を求めることができました。

まとめ

ここでは、基底を固定した表現行列$A$を射影行列によって理解することができました。対角化可能なときの場合、しかも２次元の場合についてのみ取り扱いました。

対角化可能でないときは、ちょっと工夫がいりますが（ジョルダン標準形）似たような議論ができます。興味がある人は勉強してみてください。適当な線形代数の本を読めば大抵書いてあるはずです。　

実は関数解析のスペクトルの話を勉強するときもここらへんを理解しておくと理解が進みやすいです。勉強してないとチンプンカンプンかもしれません。だから線形代数は勉強すべきですし面白いのでぜひみなさん勉強しましょう笑

---

1. ここでは、簡単のために係数体は実数全体$\mathbb{R}$にします ↩