scikit-learnを使用した主成分分析(PCA)

はじめに

こんな方にオススメ。
・説明変数の特徴量大小を把握したい
・前処理でデータの次元削減対象を知りたい
・すぐ動かせるサンプルースが知りたい

ソース

import numpy as np
import pandas as pd
import urllib.request 
import matplotlib.pyplot as plt
%matplotlib inline
import sklearn
from sklearn.decomposition import PCA #主成分分析器
from sklearn.datasets import load_iris

# データセット読み込み
iris = load_iris()
df=pd.DataFrame(iris.data, columns=iris.feature_names)
# アヤメの種類を列末に追加(3種類)
df["CLASS"]=iris.target
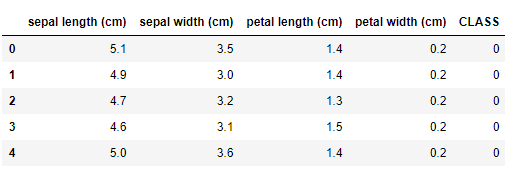
df.head()

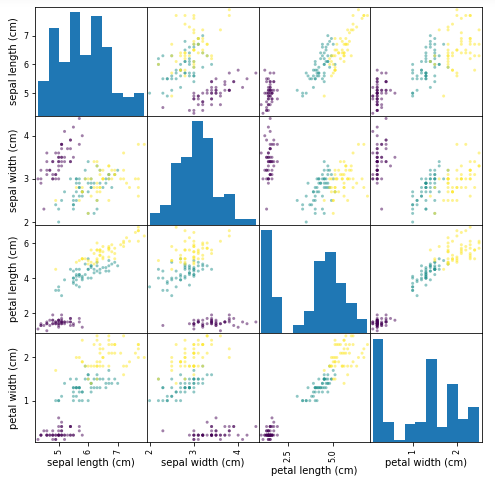
# 説明変数の組み合わせとアヤメの種類をプロット
from pandas import plotting 
plotting.scatter_matrix(df.iloc[:, 0:4], figsize=(8, 8), c=list(df.iloc[:, 4]), alpha=0.5)
plt.show()

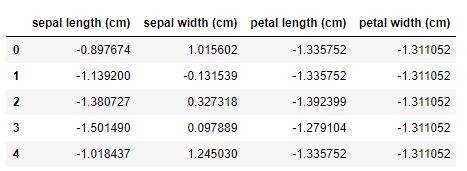
# 行列の標準化
dfs = df.iloc[:, 0:4].apply(lambda x: (x-x.mean())/x.std(), axis=0)
dfs.head()

#主成分分析
pca = PCA()
pca.fit(dfs)
feature = pca.transform(dfs)

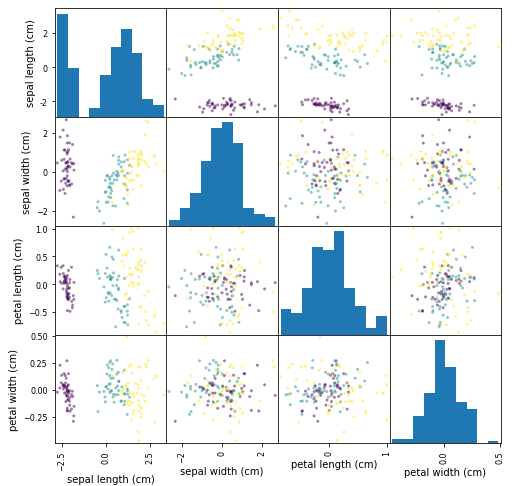
# 標準化後のプロット
from pandas import plotting 
plotting.scatter_matrix(pd.DataFrame(feature, 
                        columns=dfs.columns), 
                        figsize=(8, 8), c=list(df.iloc[:, 4]), alpha=0.5) 
plt.show()

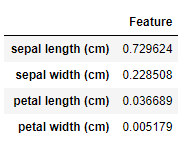
# 寄与率算出
f_df = pd.DataFrame(pca.explained_variance_ratio_, index=dfs.columns)
f_df.columns=["Feature"]
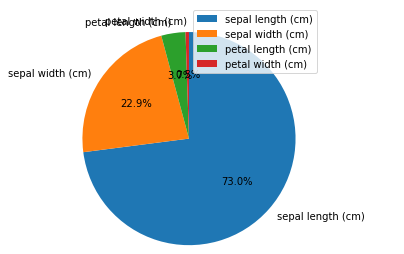
# アヤメの種類は、第二主成分までで約95%の情報を説明できる
# よって、第三、第四主成分は削減しても影響は小さいと言える
f_df

# 円グラフ表示
plt.pie(f_df, labels=f_df.index, autopct="%1.1f%%", startangle=90, counterclock=False)
plt.legend()
plt.show()

# 第一主成分と第二主成分でプロット
plt.figure(figsize=(6, 6))
plt.scatter(feature[:, 0], feature[:, 1], alpha=0.8, c=list(df.iloc[:, 4]))
plt.grid()
plt.xlabel("sepal length (cm)")
plt.ylabel("sepal width (cm)")
plt.show()

参照