はじめに
Aidemy Premium Planデータ分析講座で機械学習を学び、その成果物として東京の日照時間について時系列解析を使って予測してみました。機械学習やpythonが気になっている人や始めたばかりの人に少しでも役に立って貰えましたら嬉しいです。
動作環境
macOS Mojave Version 10.14.6
python 3.8.9
Jupytor Notebook 6.1.4
分析について
時系列分析モデル
AR, MA, ARMA, ARIMA, SARIMAモデルについて、こちらのサイトでとてもわかりやすく説明されています。
https://qiita.com/mshinoda88/items/749131478bfefc9bf365
作業内容
1. データの取得
2. データの前処理
3. データの可視化
4. パラメータの決定
5. モデル構築
6. モデルによる予測
1. データの取得
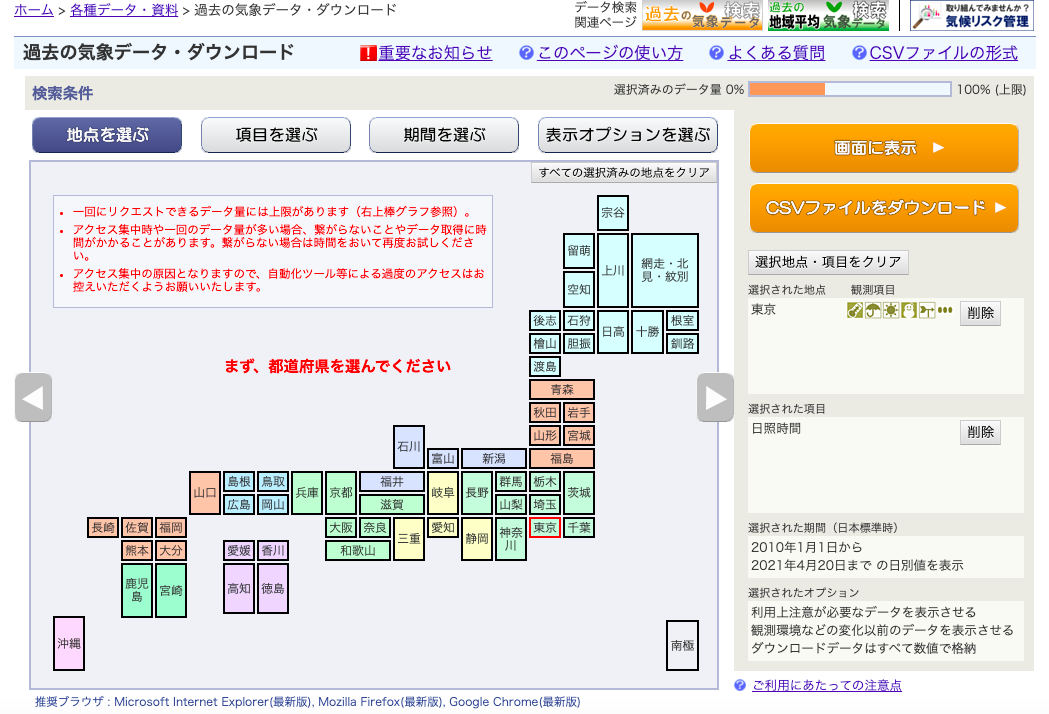
国土交通省気象庁のホームページから場所、項目、期間を設置してcsv形式でデータをダウンロードしました。
2. データの前処理
まずはデータの内容の確認です。文字コードUTF-8で作業をしたいので、データの文字コードを確認します。
import chardet
# データの読み込み
with open('./data.csv', 'rb') as f:
print('data.csv')
print(chardet.detect(f.read()))
data.csv
{'encoding': 'SHIFT_JIS', 'confidence': 0.3333333333333333, 'language': 'Japanese'}
utf-8に変換してcsvファイルに保存し直します。コードは以下のサイトを参考にしました。
import codecs
sf = codecs.open('./raw_data.csv', 'r', encoding='shift-jis')
uf = codecs.open('./raw_data_utf-8.csv', 'w', encoding='utf-8')
for line in sf:
uf.write(line)
sf.close()
uf.close()
それでは、データの内容を見ていきます。必要な情報は日付と日照時間なので、それ以外の情報を削除します。列名も余分な情報が多かったので一度削除して扱いやすいように英語に変更しました。
# データの読み込み
df = pd.read_csv('./raw_data_utf-8.csv')
# 不要な情報の削除および列名の変更
df2 = df.drop(df.index[[0, 1, 2]]).reset_index()
df2.drop(columns=df2.columns[[2, 3, 4]], inplace=True)
df2.columns=['date', 'daylight']
print(df2.head())
# データの保存
df2.to_csv('./df_data.csv', index=False)
date daylight
0 2010/1/1 9.2
1 2010/1/2 9.0
2 2010/1/3 6.6
3 2010/1/4 5.2
4 2010/1/5 8.1
情報量が多過ぎるため日毎のデータを月の平均データにしました。やり方はこちらのサイトを参考にしました。
# データの読み込み
df_data = pd.read_csv('./df_data.csv',
index_col='date',
parse_dates=True)
# マルチインデックスで「年」と「月」をセット
df_data = df_data.set_index([df_data.index.year, df_data.index.month, df_data.index])
df_data.index.names = ['year', 'month', 'date']
# 月毎に集計
summary = df_data.mean(level=('year', 'month')) # 年月単位で合計を集計する
summary = summary.reset_index() # マルチインデックスを解除する
summary['year'] = summary['year'].astype(str) # 「year」列を文字列にする
summary['month'] = summary['month'].astype(str) # 「month」列を文字列にする
# 「year」と「month」列を「-」で繋ぎ、タイムスタンプに変換する
date = pd.to_datetime(summary['year'].str.cat(summary['month'], sep='-'))
# データをSeriesで抽出する
daylight = summary['daylight']
df_data_m = pd.DataFrame({'date': date, 'daylight': daylight})
df_data_m.to_csv('./df_data_m.csv', index=False)
df_data_m = df_data_m.set_index('date')
print(df_data_m.head())
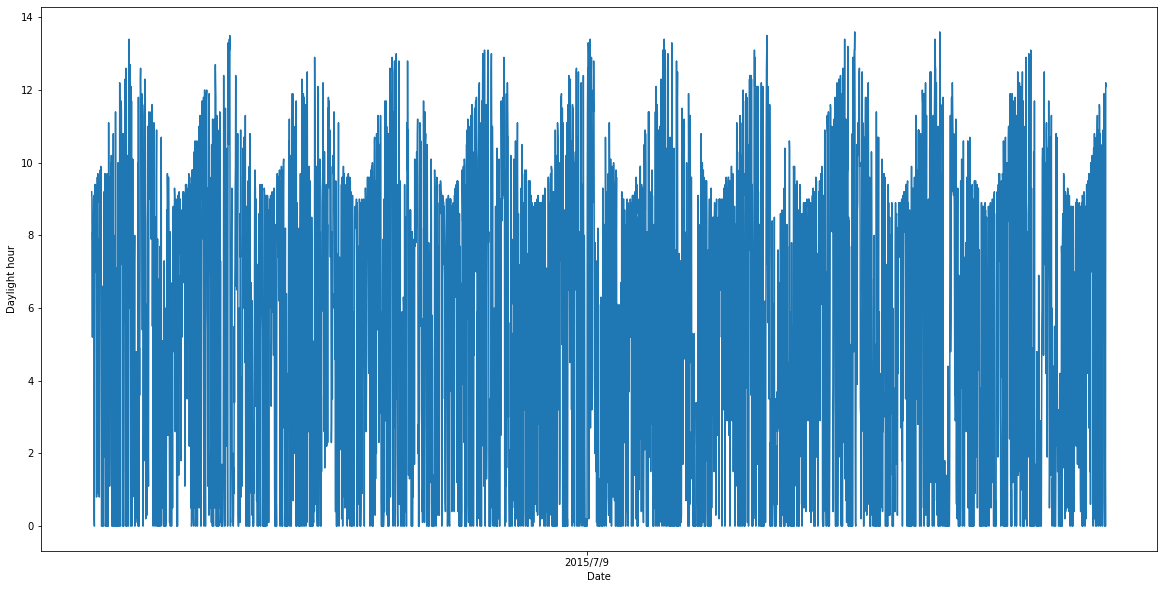
plt.figure(figsize=(20,10))
plt.xlabel("Date")
plt.ylabel("Daylight hour")
plt.plot(df_data_m)
plt.show()
daylight
date
2010-01-01 7.158065
2010-02-01 4.225000
2010-03-01 4.509677
2010-04-01 4.663333
2010-05-01 6.412903
3. データの可視化
時系列データを構成する特徴量の自己相関、トレンド、季節性、外因性、ホワイトノイズについて調べていきます。詳しくはこちらのサイトを。
https://qiita.com/hcpmiyuki/items/b1783956dee20c6d4700
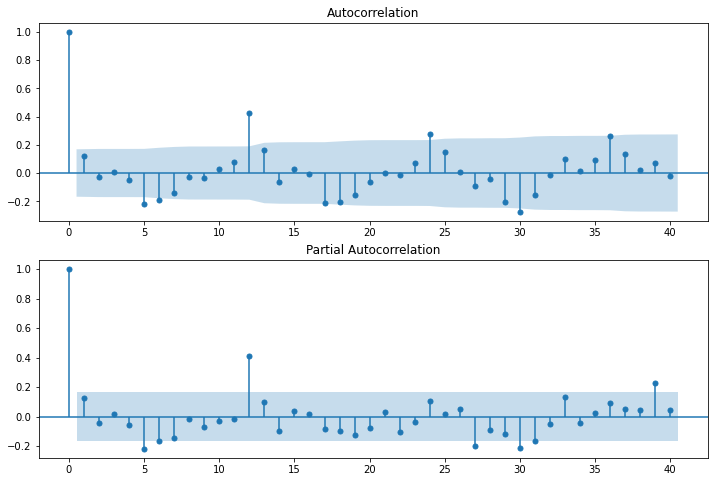
自己相関・偏自己相関
# 自己相関のグラフ
fig = plt.figure(figsize=(12,8))
ax1 = fig.add_subplot(211)
fig = sm.graphics.tsa.plot_acf(df_data['daylight'], lags=40, ax=ax1)
ax2 = fig.add_subplot(212)
fig = sm.graphics.tsa.plot_pacf(df_data['daylight'], lags=40, ax=ax2)
トレンド・周期性・残差
# データをトレンドと季節成分に分解
seasonal_decompose_res = sm.tsa.seasonal_decompose(df_data_m, freq=12)
seasonal_decompose_res.plot()
一番上が元のデータ(原系列)、二番目がトレンド、三番目が周期性、一番下が残差を示します。
4. パラメーターの決定
SARIMAモデルの最適パラメーターを決めます。今回は**ベイズ情報量基準(BIC)**を使用しました。Aidemyで使用したコードを参考にしました。
train = df_data_m[:2019-12-1]
# 最適化関数
def selectparameter(DATA, s):
p = d = q = range(0, 3)
pdq = list(itertools.product(p, d, q))
seasonal_pdq = [(x[0], x[1], x[2], s) for x in list(itertools.product(p, d, q))]
parameters = []
BICs = np.array([])
for param in pdq:
for param_seasonal in seasonal_pdq:
try:
mod = sm.tsa.statespace.SARIMAX(DATA,
order=param,
seasonal_order=param_seasonal)
results = mod.fit()
parameters.append([param, param_seasonal, results.bic])
BICs = np.append(BICs, results.bic)
except:
continue
return parameters[np.argmin(BICs)]
best_params = selectparameter(train, 12)
print(best_params)
[(0, 0, 0), (0, 1, 1, 12), 387.4500999332838]
このパラメーターを使ってモデルを作成します。
5. モデル作成
決定したパラメーターをstatsmodelsのSARIMAXのorderと**に入力して作成します。
# トレーニングデータとテストデータに切り分け
pre_train = df_data_m[:119] #2019-12-01までを使用
train = pre_train.set_index('date')
pre_test = df_data_m[120:] #2020-01-01までを使用
test_date = pre_test['date']
test = pre_test['daylight']
test.rename(index=test_date, inplace=True)
# モデルの構築
SARIMA_model = sm.tsa.statespace.SARIMAX(train, order=(0, 0, 0),
seasonal_order=(0, 1, 1, 12),
enforce_stationarity=False, enforce_invertibility=False).fit()
print(SARIMA_model.summary())
SARIMAX Results
==================================================================================
Dep. Variable: daylight No. Observations: 119
Model: SARIMAX(0, 1, [1], 12) Log Likelihood -132.385
Date: Thu, 22 Apr 2021 AIC 268.771
Time: 11:10:56 BIC 273.858
Sample: 01-01-2010 HQIC 270.826
- 11-01-2019
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
ma.S.L12 -0.7653 0.069 -11.035 0.000 -0.901 -0.629
sigma2 0.9286 0.105 8.832 0.000 0.722 1.135
===================================================================================
Ljung-Box (L1) (Q): 1.08 Jarque-Bera (JB): 16.49
Prob(Q): 0.30 Prob(JB): 0.00
Heteroskedasticity (H): 2.39 Skew: -0.77
Prob(H) (two-sided): 0.02 Kurtosis: 4.35
===================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
6. モデルによる予測
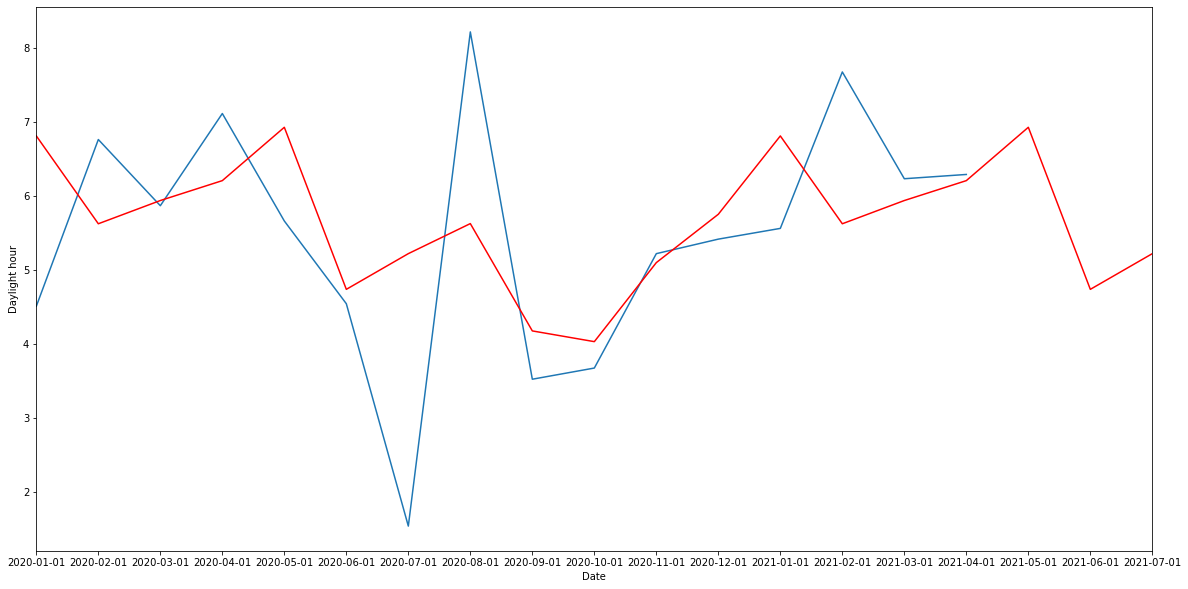
最後にこのモデルを使って予測してみました。
グラフ化時に”tzinfo argument must be None or of a tzinfo subclass, not type 'UnitData'”エラーを出したので、日付を付け直し手からグラフ化しました。
# 予測
pred = SARIMA_model.predict('2020-01-01', '2021-07-01')
# predの日付の付け直し
from dateutil.relativedelta import relativedelta
datetime.datetime(2016, 12, 1) + relativedelta(months=1)
d = datetime.datetime(2020, 1, 1)
td = relativedelta(months=1)
n = 19
f = '%Y-%m-%d'
l = []
for i in range(n):
l.append((d + i * td).strftime(f))
df_date = pd.DataFrame(l)
df_date.columns = ['date']
df_pred = pd.DataFrame(pred).reset_index()
pred_date = df_pred.join(df_date, how='outer')
print(pred_date)
pred_date2 = pred_date[["predicted_mean", "date"]]
date_pred = pred_date2.set_index('date')
# testの日付の付け直し
df_test = pd.DataFrame(test).reset_index()
test_date = df_test.join(df_date, how='outer')
test_date2 = test_date[["daylight", "date"]]
date_test = test_date2.set_index('date')
date_test2 = date_test.dropna(how='any', axis=0)
print(date_test2)
# 予測結果のグラフ化
plt.figure(figsize=(20,10))
plt.plot(date_test2)
plt.plot(date_pred, "r")
plt.xlabel("Date")
plt.ylabel("Daylight hour")
plt.xlim(['2020-01-01','2021-07-01'])
plt.show()
さらにモデルの予測精度をRMSE(二乗平均平方根誤差)で評価しました。
rmse = np.sqrt(((pred - test) ** 2).mean())
print('RMSE = {}'.format(round(rmse, 4)))
RMSE = 1.4971
十分低い値が出ましたので、結構良いモデルができたのではないかと思います。
終わりに
成果物として今回一人でやっていましたが、pythonを使ったプログラミング力だけでなく、分析自身の知識が全く足りないことを実感できました。今後は経験をもっと積み上げていき精度の高いものを目指していきたいと思いました。
python初心者の方にこんな方法があると知って貰えたら幸いです。