これはMYJLab Advent Calendar 2019の14日目の記事です。
こんにちは
- 宮治研究室に所属する学部3年、サッチーと呼ばれています
- webとか機械学習は周りのつよつよな方々が書いてくださるので、私は統計っぽいことを書きます
今回は
すること
Pythonのライブラリであるstatsmodelsを用いて時系列分析の基本であるBox-Jenkins法を用いた分析の一連の流れを実装していきます。
時系列分析はPythonの文献がなぜか少ないのが悲しいので、Pythonで時系列分析入門したい人のお役に立てれば幸いです。
しないこと
長くなってしまうので定常過程や単位根検定の種類等、手法の細かい説明は省きます。あくまでも実装メインで進めていきます。理論部分は有名なlogics of blueさんのものがとても優しくてわかりやすいかと思います。
statsmodelsとは
統計モデルの実装のために必要なものがたくさん揃っている便利すぎるライブラリです。scikit-learnみたいな感じですが、scikit-learnの方が機械学習寄りでstatsmodelsの方が統計寄りという印象です。
いざ分析
実行環境
- Jupyter Notebook
- Python 3.7.3
流れ
- 使用するデータを確認、時系列分析の基本説明
- データを定常な状態にする
- モデル推定
- 実際にアイスの売り上げ予測
使用するデータ
いい感じにわかりやすいトレンドや季節性があるデータが欲しかったので色々ググってみたら金沢のアイスクリームの売り上げが出てきたのでそれと月ごとの平均気温を合わせてデータを作りました。requestsで落とせるようにしてあります。出典は以下に記載してあります。
もろもろ読み込みます
使用するライブラリ
import statsmodels.api as sm
import pandas as pd
import numpy as np
import requests
import io
from matplotlib import pylab as plt
%matplotlib inline
# グラフを横長にする
from matplotlib.pylab import rcParams
rcParams['figure.figsize'] = 15, 6
グラフはあらかじめ横長めに固定しておきます
データ
URL = "https://drive.google.com/uc?id=1MZMKbSQXeVnlAWijTC_hwFCCxPbYNX-Y"
r = requests.get(URL)
row_data = pd.read_csv(io.BytesIO(r.content))
google driveの共有リンクからデータを落とす方法はこちらの記事を参考にしました。
row_data.head()
 earningsがiceの売り上げ、temperatureがその月の平均気温になっています。このデータフレームを分析できる形に変えていきます。
earningsがiceの売り上げ、temperatureがその月の平均気温になっています。このデータフレームを分析できる形に変えていきます。
# float型にしないとモデルを推定する際にエラーがでる
row_data.earnings = row_data.earnings.astype('float64')
row_data.temperature = row_data.temperature.astype('float64')
# datetime型にしてインデックスにする
row_data.date = pd.to_datetime(row_data.date)
data = row_data.set_index("date")
変形後のデータフレームを確認
data.head()

データの全体像を確認
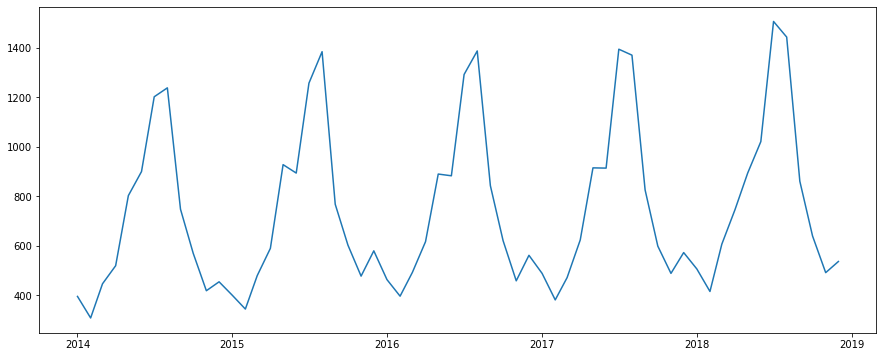
plt.plot(data.earnings)
申し訳ないくらい特徴がわかりやすいデータですね。
これでデータの準備はできました。それではこれからアイスの売り上げを予測するモデルを作っていきますが、まずは時系列データを取り扱う際に大切な考え方を軽く説明します。
時系列データは1.自己相関、2.周期性、3.トレンド、4.外因性、5.ホワイトノイズ の5つに分解して説明することができます。
- 自己相関
時系列上にある異なる点同士の相関のことを自己相関と言います。時系列分析がただの回帰分析と大きく違うのがデータの前後の関係を考慮する点です。自己相関を用いることで、データの前後の関係を表現します。
自己相関はコレログラムというグラフで表すことができます。statsmodelsではgraphicsのplot_acfでコレログラムを描画することができます。また、今回は割愛しますが、自己相関と似ているもので、「偏自己相関」というものがあります。偏自己相関はplot_pacfで描画することができます。
今回のデータの自己相関を図で表すとこのようになります。
# 自己相関のグラフ
fig = plt.figure(figsize=(12,8))
ax1 = fig.add_subplot(211)
fig = sm.graphics.tsa.plot_acf(data.earnings, lags=40, ax=ax1)
ax2 = fig.add_subplot(212)
fig = sm.graphics.tsa.plot_pacf(data.earnings, lags=40, ax=ax2)
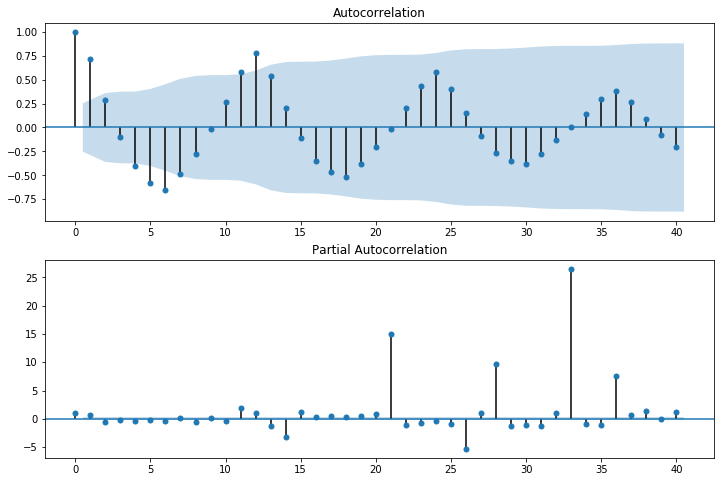
「AutoCorrelation」がコレログラムです。ちなみに水色になっている部分は95%信頼区間を表しています。この信頼区間外にデータが及んでいる点は統計的に有意差があると言えます。横軸が12、24、36の時に大きくなっており、12ヶ月前のデータと似ているということがわかります。つまり12ヶ月ごとの周期性があるということになります。
-
周期性
周期性は季節性とも言います。12ヶ月周期で似た変化をしたり、曜日によって周期的な変化をしたりすることをさします。今回のアイスのデータで言えば12ヶ月周期の季節性がありそうです。 -
トレンド
トレンドはそのままですが、全体の傾向という感じです(結局説明になってなくて申し訳ないです)。今回で言えば、なんとなく上昇傾向があるように見えます。 -
外因性
1.~3.まではデータの中での特徴でしたが、外因性は自己相関だけでは説明できないデータの動きのことを指します。例えば人気番組でアイスの特集が組まれたことでアイスが売れるようになった、みたいな感じです。 -
ホワイトノイズ
これまで述べたデータの特徴以外で説明不可能なノイズをホワイトノイズと言います。残差とかとも言います。
statsmodelsのseasonal_decomposeを使うと、サクッと時系列データをトレンド成分と周期成分と残差に分解することができます。しかもそのままプロットできる・・・!
# データをトレンドと季節成分に分解
seasonal_decompose_res = sm.tsa.seasonal_decompose(data.earnings, freq=12)
seasonal_decompose_res.plot()
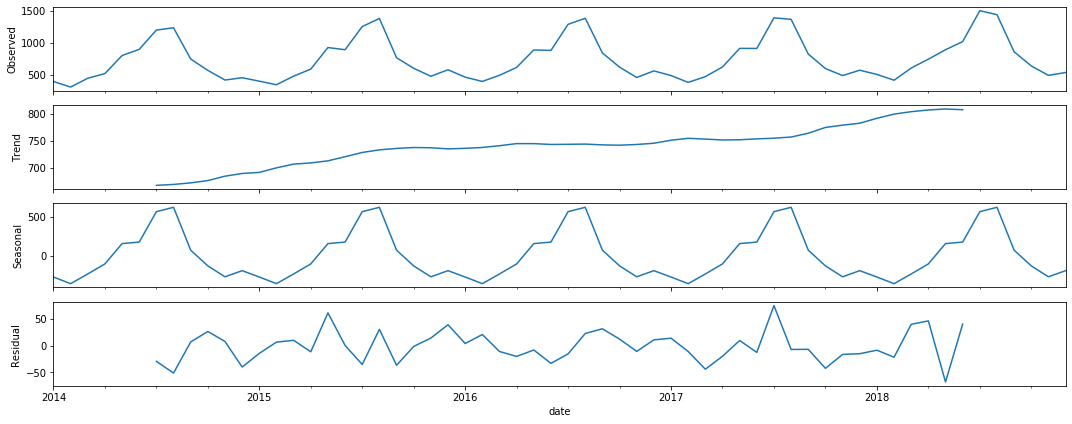
Observedが元のデータで、下の3つが分解した成分です。予想通り、右肩上がりのトレンドと12ヶ月の周期性がありそうです。
トレンドと季節性があるデータは「SARIMA」モデルというモデルで表現することができます。また、今回は外因性として月ごとの平均気温を用意したので、外因性を考慮することができる「SARIMAX」モデルを採用します。ちなみに平均気温自体が売り上げデータの周期性とほぼ同様の変化をするはずなので正直外因性として盛り込む意味はあまりないのですが、今回は外因性を扱う手法を紹介するために取り入れていきます。
データを定常にしていく
細かい説明は割愛しますが、トレンド成分が含まれているデータは「非定常」であるといい、分析がしにくい状態になっています。それに対して「定常」なデータは分析がしやすいのでデータを定常な状態にしたいです。通常、非定常なデータは差分をとることでトレンド成分を取り除き、定常にすることができます。また、データが定常であるかは「単位根検定」を行うことで調べることができます。
試しに、差分を取らずに原系列で単位根検定を行ってみます。今回はADF種類の単位根検定を用いました。
# トレンド項あり(1次まで)、定数項あり
ct = sm.tsa.stattools.adfuller(data.earnings, regression="ct")
# トレンド項なし、定数項あり
c = sm.tsa.stattools.adfuller(data.earnings, regression="c")
# トレンド項なし、定数項なし
nc = sm.tsa.stattools.adfuller(data.earnings, regression="nc")
print("ct:")
print(ct[1])
print("---------------------------------------------------------------------------------------------------------------")
print("c:")
print(c[1])
print("---------------------------------------------------------------------------------------------------------------")
print("nc:")
print(nc[1])
print("---------------------------------------------------------------------------------------------------------------")
# 出力
ct:
0.881744298708034
---------------------------------------------------------------------------------------------------------------
c:
0.8192957538918915
---------------------------------------------------------------------------------------------------------------
nc:
0.9999999896927978
---------------------------------------------------------------------------------------------------------------
出力結果の値はP値を表しています。ADF検定ではデータが単位根過程であることが帰無仮説になっていているので、棄却することができればデータが単位根過程でない、つまり定常であると判断できます。
原系列では全ての場合においてP値を棄却できないため、非定常であると言えます。
次にデータを1ずつずらして差分をとってみます。diff()で階差1,diff(2)で階差2の差分が取れます。ずらした分欠損値ができるので、それは取り除きます。
diff = data.earnings.diff()
diff = diff.dropna()
# トレンド項あり(1次まで)、定数項あり
ct = sm.tsa.stattools.adfuller(diff, regression="ct")
# トレンド項なし、定数項あり
c = sm.tsa.stattools.adfuller(diff, regression="c")
# トレンド項なし、定数項なし
nc = sm.tsa.stattools.adfuller(diff, regression="nc")
print("ct:")
print(ct[1])
print("---------------------------------------------------------------------------------------------------------------")
print("c:")
print(c[1])
print("---------------------------------------------------------------------------------------------------------------")
print("nc:")
print(nc[1])
print("---------------------------------------------------------------------------------------------------------------")
# 出力
ct:
0.005220302847135729
---------------------------------------------------------------------------------------------------------------
c:
0.0006567788221081102
---------------------------------------------------------------------------------------------------------------
nc:
0.0019344470286669219
---------------------------------------------------------------------------------------------------------------
全部棄却できた・・・!
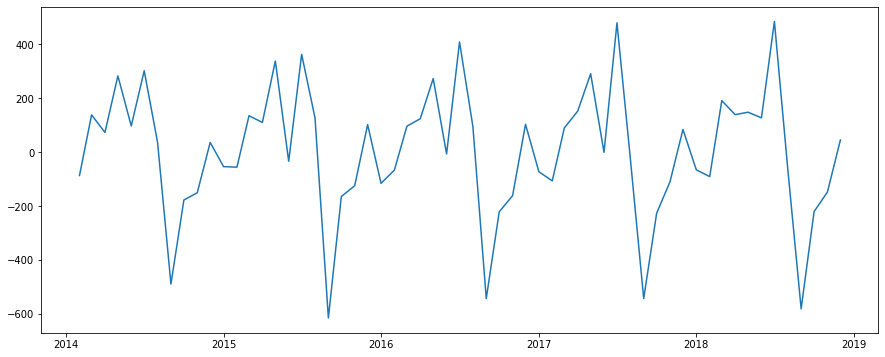
ちなみに差分系列をプロットするとこんな感じになります。
plt.plot(diff)
原系列には右肩上がりのトレンドがありましたが、差分系列は平均が一定っぽい感じになりました!
モデル推定
データが定常になればあとはstatsmodelsのSARIMAXを使ってモデルを推定するだけです。SARIMAXモデルの少し難しい点が、トレンドや周期性を表現できる分、設定するパラメータが多くなってしまうことです。今回はAICという指標を用いて、パラメータを半自動的に推定します。(これはとてもよくある手法です)
まず、データをトレーニングデータとテストデータに分割します。
train_data = data[data.index < "2018-06"]
# テストデータはテスト期間以前の日付も含まなければいけない
test_data = data[data.index >= "2018-05"]
次にパラメータ推定をします。周期性は12であることが推定できるので、それ以外のパラメータだけ総当たりで計算し、AICが最小のものを採用します。
# 総当たりで、AICが最小となるSARIMAの次数を探す
max_p = 3
max_q = 3
max_d = 2
max_sp = 1
max_sq = 1
max_sd = 1
pattern = max_p*(max_d + 1)*(max_q + 1)*(max_sp + 1)*(max_sq + 1)*(max_sd + 1)
modelSelection = pd.DataFrame(index=range(pattern), columns=["model", "aic"])
# 自動SARIMA選択
num = 0
for p in range(1, max_p + 1):
for d in range(0, max_d + 1):
for q in range(0, max_q + 1):
for sp in range(0, max_sp + 1):
for sd in range(0, max_sd + 1):
for sq in range(0, max_sq + 1):
sarima = sm.tsa.SARIMAX(
train_data.earnings, order=(p,d,q),
seasonal_order=(sp,sd,sq,12),
enforce_stationarity = False,
enforce_invertibility = False
).fit()
modelSelection.ix[num]["model"] = "order=(" + str(p) + ","+ str(d) + ","+ str(q) + "), season=("+ str(sp) + ","+ str(sd) + "," + str(sq) + ")"
modelSelection.ix[num]["aic"] = sarima.aic
num = num + 1
この実行には数分かかることがあります。
実行が終わったら、できたデータフレームからAICが小さいものを検索します
modelSelection.sort_values(by='aic').head()

パラメータが3,2,2,1,1,0のモデルがAICが最小になるようなので、これを採用してモデルを推定してみます。
モデルの推定は以下の1行のみでできてしまいます。
SARIMA_3_2_2_110 = sm.tsa.SARIMAX(train_data.earnings, order=(3,2,2), seasonal_order=(1,1,0,12)).fit()
モデルの評価にはLjungbox検定を用います。これも細かい説明は割愛しますが、この検定は「残差に有意な自己相関が1つもない」(厳密にいうと違うのですが・・・)ことが帰無仮説なので、棄却されないと嬉しいです。残差に有意な自己相関があるということはまだ説明仕切れていないデータの特徴が存在するということになります。model.residで残差を得ることができます。
# Ljungbox検定
ljungbox_result = sm.stats.diagnostic.acorr_ljungbox(SARIMA_3_2_2_110.resid, lags=10)
df_ljungbox_result = pd.DataFrame({"p-value":ljungbox_result[1]})
df_ljungbox_result[df_ljungbox_result["p-value"] < 0.05]
棄却したくないのでこのコードの出力結果は空のデータフレームであって欲しいのですが・・・
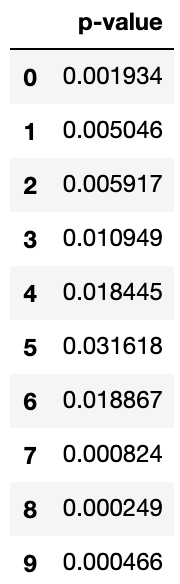
残念ながら全てのラグでP値が0.05より小さく、帰無仮説は棄却されてしまいました。AICが低ければ必ずしもいいモデルという訳ではないので仕方ないです。
ということで色々試してみた結果、
# モデル推定
SARIMA_3_1_3_110 = sm.tsa.SARIMAX(train_data.earnings, order=(3,1,3), seasonal_order=(1,1,0,12)).fit()
# 残差の検定
ljungbox_result = sm.stats.diagnostic.acorr_ljungbox(SARIMA_3_1_3_110.resid, lags=10)
# 結果
df_ljungbox_result = pd.DataFrame({"p-value":ljungbox_result[1]})
df_ljungbox_result[df_ljungbox_result["p-value"] < 0.05]
AICが4番目に低いパラメータでLjungbox検定をクリアすることができました!
売り上げ予測してみる
できたモデルを使ってテスト期間の売り上げを予測してみます
# 予測
pred = SARIMA_3_1_3_110.predict('2018-05-01', '2018-12-01')
# 実データと予測結果の図示
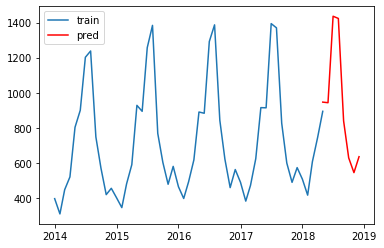
plt.plot(train_data.earnings, label="train")
plt.plot(pred, "r", label="pred")
plt.legend()
正解データと一緒にプロットしてみます
# 予測評価
pred = SARIMA_3_1_3_110.predict('2018-05-01', '2018-12-01')
# 実データと予測結果の図示
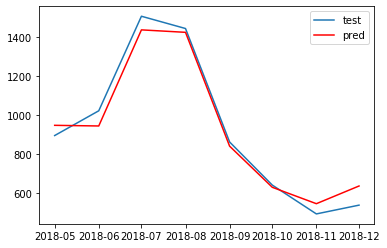
plt.plot(test_data.earnings, label="test")
plt.plot(pred, "r", label="pred")
plt.legend()
それっぽいですね~~
おまけ
先ほども述べたように、SARIMAXモデルは外因性を考慮することができる
今回は平均気温だけだが、複数の外因性を引数に取ることもできます。優秀
SARIMA_3_1_3_110_with_exog = sm.tsa.SARIMAX(train_data.earnings, train_data.temperature, order=(3,1,3), seasonal_order=(1,1,0,12)).fit()
ちなみに結果は
# 予測
# データを(7, 1)に変形する
test_temperature = [[test_data.temperature[i+1]] for i in range(7)]
pred_with_exog = SARIMA_3_1_3_110_with_exog.predict('2018-05-01', '2018-12-01', exog=test_temperature)
# 実データと予測結果の図示
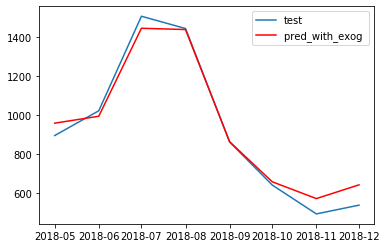
plt.plot(test_data.earnings, label="test")
plt.plot(pred_with_exog , "r", label="pred_with_exog ")
plt.legend()
やはりそんなに変わらなかった。
終わりに
雑ですが一通りの時系列分析の流れを紹介させていただきました。statsmodelsは本当に便利なライブラリなのでこれを使って素敵な時系列分析ライフを送っていただけると幸いです。拙い文章でしたが最後までお読みいただきありがとうございました。何かご指摘があればコメントしてください。
おやすみなさい。
出典
- 気象庁 金沢の年毎の平均気温(http://www.data.jma.go.jp/obd/stats/etrn/view/annually_s.php?prec_no=56&block_no=47605&year=&month=&day=&view=)
- 日本アイスクリーム協会 金沢アイスクリーム調査報告書(https://www.icecream.or.jp/biz/data/expenditures.html)