はじめに
やりたいことは python3 で時系列分析を行い、予測までしてみること。
特に季節変動を加味したSARIMAモデルを扱ってみたい。
利用するデータとしては、以下の参考資料で、TV朝日の視聴率の時系列分析をしてみる。
きっかけは2016年度4Qで大きく利益率を落としているが、視聴率変動がどう影響しているのか、今後の変動はどう予測できるのかを試行した。
参考資料
http://www.tv-asahihd.co.jp/contents/ir_setex/
未来を予測するビッグデータの解析手法と「SARIMAモデル」 - DeepAge
https://deepage.net/bigdata/2016/10/22/bigdata-analytics.html
SARIMA モデルの概要
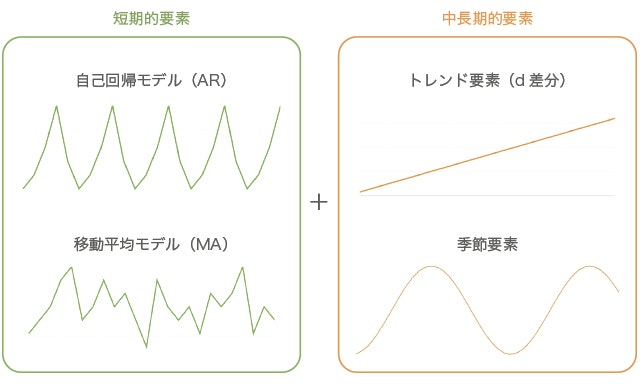
SARIMAモデルは複数の時系列モデルを複合した手法。
以下の図のような関係があります。
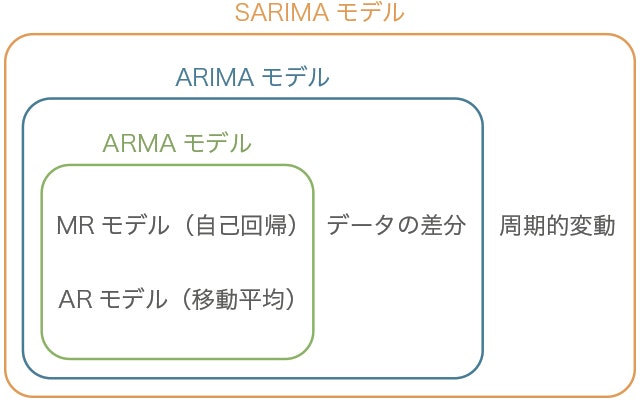
(出典: 未来を予測するビッグデータの解析手法と「SARIMAモデル」 - DeepAge)
ARモデル(自己回帰モデル, autoregressive model)
ARモデルは図のように時間の変化に対し規則的に値が変化する、最も単純な時系列モデル。
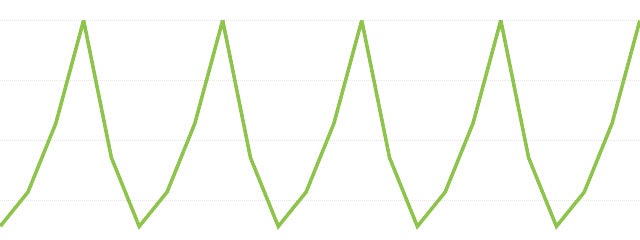
直前のp個の値と相関のあるモデルをAR(p)と表現します。
ARモデルはある時点のデータがそれ以前のデータで回帰的に推定できるモデルです。
MAモデル(移動平均モデル、Moving Average model)
MAモデルは図のように時間の変化に対し不規則に値が変化するけど、
ある区間での変動が一定であるようにモデルを考えます。
直前のq個の値の誤差の影響を受けるモデルをMA(q)と表現します。
MAモデルは過去の誤差に影響されるモデルです。
ARMAモデル(自己回帰移動平均モデル)
ARモデルとMAモデルの2つ組み合わせて定式化したモデル。
ARモデルに関連する次数をpとMAモデルに関連する次数をqとすると、ARMA(p,q)と表すことができます。
定常性
ARモデル、MAモデル、ARMAモデルはいずれも定常過程を対象とした時系列モデル。
定常過程は、以下の二つを満たすものを言います。
・平均が時間に依存せずに一定である
・異時点間の共分散が時間差のみに依存する
つまり、定常性のある時系列データは「一定の周期で同程度の変動をしている」といえます。
時系列において、平均値が時間的に常に一定であることが保証されているのは稀。
つまり現実に扱う時系列データは非定常過程であることが多い。
実用に際しては、非定常過程の時系列データを対象とした手法を用いる必要があります。
そこで、SARIMAの出番です。
SARIMAモデル(季節自己回帰和分移動平均モデル)
(出典: 未来を予測するビッグデータの解析手法と「SARIMAモデル」 - DeepAge)
最後は少しはしょりましたが、本題にGo.
データを準備する
# 基本のライブラリを読み込む
import numpy as np
import pandas as pd
from scipy import stats
# グラフ描画
from matplotlib import pylab as plt
import seaborn as sns
%matplotlib inline
# グラフを横長にする
from matplotlib.pylab import rcParams
rcParams['figure.figsize'] = 15, 6
import matplotlib as mpl
mpl.rcParams['font.family'] = ['serif']
url = "/work/02_timeseries/tvasahi201701.txt"
file2 = "/work/02_timeseries/tvasahi201701_2.txt"
dataNormal = pd.read_csv(url)
dataNormal.head()

全日、ゴールデン、プライム、プライム2の時間帯で視聴率データが揃えられる。
今回はプライムタイムのみのデータを利用して分析してみる。なぜこのデータをチョイスしたかというとトレンドがはっきり現れていて、データ分析、予測の学習にはもってこいだから。
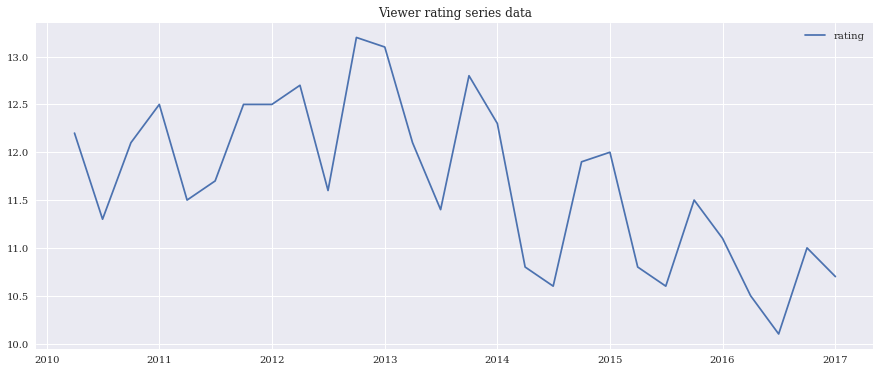
まず、このデータをプロットしてみる。
ts = ((dataNormal.T)[2])
dateparse = lambda dates: pd.datetime.strptime(dates, '%Y-%m-01')
ts = pd.read_csv(file2, index_col="time", date_parser=dateparse, dtype='float')
plt.plot(ts, label='rating')
plt.title('Viewer rating series data')
plt.legend(loc='best')
Dickey-Fuller test
定常性をチェックするための統計的テストの1つです。
ここで、帰無仮説は、ts が非定常であるということ。
テスト結果は、「検定統計量(Test Statistic)」と1,5,10%の信頼水準の「臨界値(Critical Value)」から構成されます。
「検定統計量」が「臨界値」よりも小さい場合は、帰無仮説を棄却して系列が定常状態と判定できます。
from statsmodels.tsa.stattools import adfuller
# Dickey-Fuller test 結果と標準偏差、平均のプロット
def test_stationarity(timeseries, window_size=12):
# Determing rolling statistics
rolmean = timeseries.rolling(window=window_size,center=False).mean()
rolstd = timeseries.rolling(window=window_size,center=False).std()
# Plot rolling statistics:
orig = plt.plot(timeseries, color='blue',label='Original')
mean = plt.plot(rolmean, color='red', label='Rolling Mean')
std = plt.plot(rolstd, color='black', label = 'Rolling Std')
plt.legend(loc='best')
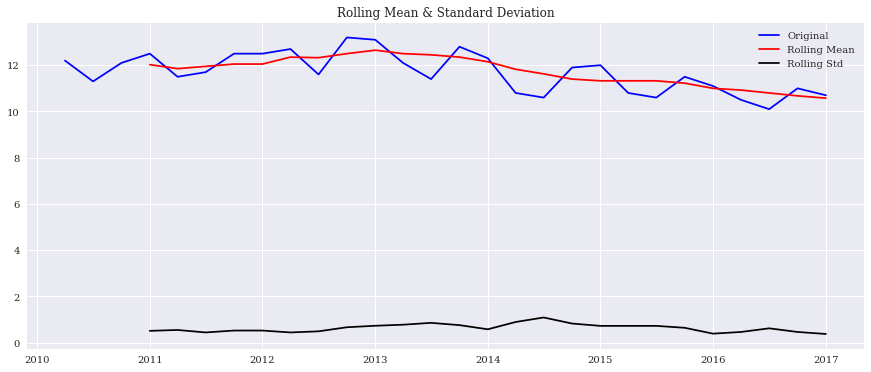
plt.title('Rolling Mean & Standard Deviation')
plt.show(block=False)
# Perform Dickey-Fuller test:
print('Results of Dickey-Fuller Test:')
dftest = adfuller(timeseries, autolag='AIC')
dfoutput = pd.Series(dftest[0:4], index=['Test Statistic','p-value',
'#Lags Used','Number of Observations Used'])
for key,value in dftest[4].items():
dfoutput['Critical Value (%s)'%key] = value
print(dfoutput)
まずは上記関数を呼び出してみる。
test_stationarity(ts, window_size=4)
Results of Dickey-Fuller Test:
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
<ipython-input-8-552a0eb0606f> in <module>()
----> 1 test_stationarity(ts, window_size=4)
<ipython-input-7-e5ce27c1c7e1> in test_stationarity(timeseries, window_size)
17 # Perform Dickey-Fuller test:
18 print('Results of Dickey-Fuller Test:')
---> 19 dftest = adfuller(timeseries, autolag='AIC')
20 dfoutput = pd.Series(dftest[0:4], index=['Test Statistic','p-value',
21 '#Lags Used','Number of Observations Used'])
/root/anaconda3/lib/python3.6/site-packages/statsmodels/tsa/stattools.py in adfuller(x, maxlag, regression, autolag, store, regresults)
218
219 xdiff = np.diff(x)
--> 220 xdall = lagmat(xdiff[:, None], maxlag, trim='both', original='in')
221 nobs = xdall.shape[0] # pylint: disable=E1103
222
/root/anaconda3/lib/python3.6/site-packages/statsmodels/tsa/tsatools.py in lagmat(x, maxlag, trim, original, use_pandas)
373 if xa.ndim == 1:
374 xa = xa[:, None]
--> 375 nobs, nvar = xa.shape
376 if original in ['ex', 'sep']:
377 dropidx = nvar
ValueError: too many values to unpack (expected 2)
エラーが出てしまいました。
標準偏差は大きく変動していないけど、移動平均は緩やかに下落している模様。
対数をとって傾向を確認
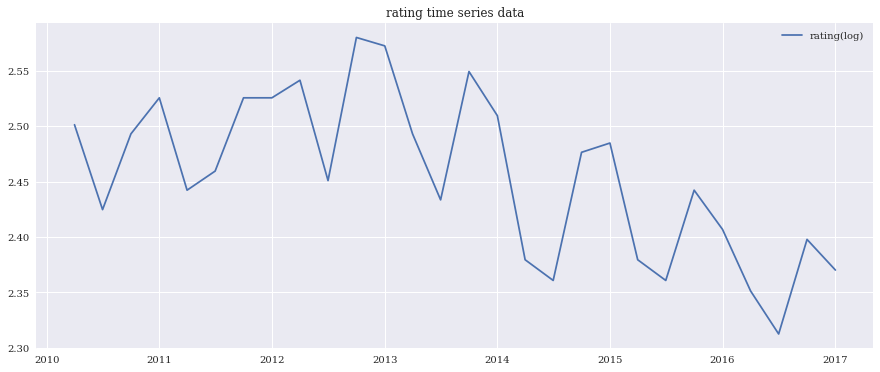
次に対数をとって傾向を確認して見ましょう。
ts_log = np.log(ts)
plt.plot(ts_log, label='rating(log)')
plt.title('rating time series data')
plt.legend(loc='best')
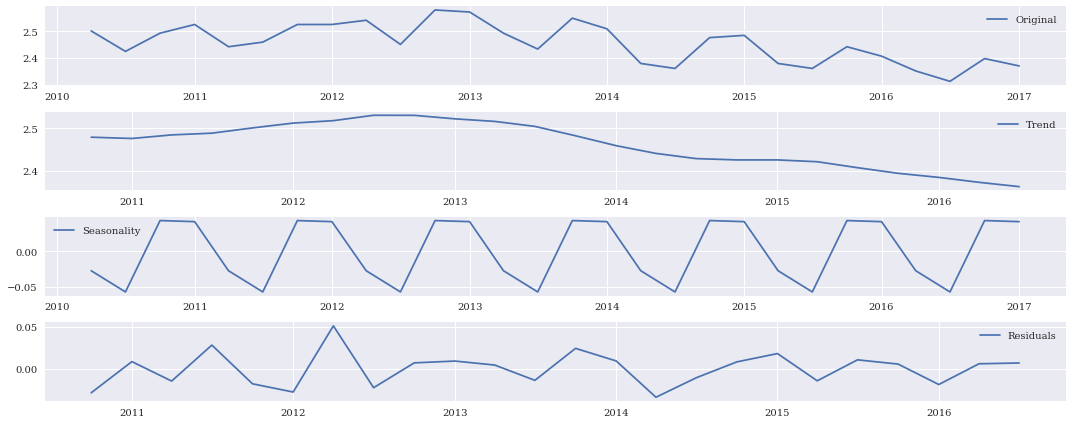
次に対数データについて、傾向、季節性、残差を眺めてみる。
# 傾向(trend)、季節性(seasonal)、残差(residual)に分解してモデル化する。
from statsmodels.tsa.seasonal import seasonal_decompose
decomposition = seasonal_decompose(ts_log)
trend = decomposition.trend
seasonal = decomposition.seasonal
residual = decomposition.resid
# オリジナルの時系列データプロット
plt.subplot(411)
plt.plot(ts_log, label='Original')
plt.legend(loc='best')
# trend のプロット
plt.subplot(412)
plt.plot(trend, label='Trend')
plt.legend(loc='best')
# seasonal のプロット
plt.subplot(413)
plt.plot(seasonal,label='Seasonality')
plt.legend(loc='best')
# residual のプロット
plt.subplot(414)
plt.plot(residual, label='Residuals')
plt.legend(loc='best')
plt.tight_layout()
秋にかけて視聴率が下がり、冬に視聴率が上がるというのが毎年の季節性のある傾向。
トレンドとしては緩やかに下がってきているのが見て取れます。
SARIMAモデルの最適なパラメータを探す
SARIMA モデルを以下のライブラリでオブジェクト化してみるが、
http://www.statsmodels.org/dev/generated/statsmodels.tsa.statespace.sarimax.SARIMAX.html
sarima = sm.tsa.SARIMAX(
ts, order=(p,d,q),
seasonal_order=(sp,sd,sq,4),
enforce_stationarity = False,
enforce_invertibility = False)
p,d,q,sp,sd,sq の組み合わせを探してみる。
(sp,sd,sq,4)の最後の4は年間を四半期に分けているので分割数4と指定しています。
import statsmodels.api as sm
# 自動SARIMA選択
num = 0
for p in range(1, max_p + 1):
for d in range(0, max_d + 1):
for q in range(0, max_q + 1):
for sp in range(0, max_sp + 1):
for sd in range(0, max_sd + 1):
for sq in range(0, max_sq + 1):
sarima = sm.tsa.SARIMAX(
ts, order=(p,d,q),
seasonal_order=(sp,sd,sq,4),
enforce_stationarity = False,
enforce_invertibility = False
).fit()
modelSelection.iloc[num]["model"] = "order=(" + str(p) + ","+ str(d) + ","+ str(q) + "), season=("+ str(sp) + ","+ str(sd) + "," + str(sq) + ")"
modelSelection.iloc[num]["aic"] = sarima.aic
num = num + 1
# モデルごとの結果確認
print(modelSelection)
# AIC最小モデル
print(modelSelection[modelSelection.aic == min(modelSelection.aic)])
以下が実行結果。
model aic
0 order=(1,0,0), season=(0,0,0) 70.3877
1 order=(1,0,0), season=(0,0,1) 48.7876
2 order=(1,0,0), season=(0,1,0) 40.1175
3 order=(1,0,0), season=(0,1,1) 27.9964
4 order=(1,0,0), season=(1,0,0) 40.728
5 order=(1,0,0), season=(1,0,1) 37.2894
6 order=(1,0,0), season=(1,1,0) 30.3103
7 order=(1,0,0), season=(1,1,1) 29.522
8 order=(1,0,1), season=(0,0,0) 62.5256
9 order=(1,0,1), season=(0,0,1) 43.3847
10 order=(1,0,1), season=(0,1,0) 37.7301
11 order=(1,0,1), season=(0,1,1) 26.0388
12 order=(1,0,1), season=(1,0,0) 41.8186
13 order=(1,0,1), season=(1,0,1) 32.2768
14 order=(1,0,1), season=(1,1,0) 31.8695
15 order=(1,0,1), season=(1,1,1) 28.0252
16 order=(1,0,2), season=(0,0,0) 57.7646
17 order=(1,0,2), season=(0,0,1) 40.7138
18 order=(1,0,2), season=(0,1,0) 36.0716
19 order=(1,0,2), season=(0,1,1) 25.3384
20 order=(1,0,2), season=(1,0,0) 42.2375
21 order=(1,0,2), season=(1,0,1) 28.2212
22 order=(1,0,2), season=(1,1,0) 33.8669
23 order=(1,0,2), season=(1,1,1) 27.4596
24 order=(1,0,3), season=(0,0,0) 57.36
25 order=(1,0,3), season=(0,0,1) 39.7003
26 order=(1,0,3), season=(0,1,0) 37.0603
27 order=(1,0,3), season=(0,1,1) 24.85
28 order=(1,0,3), season=(1,0,0) 45.7587
29 order=(1,0,3), season=(1,0,1) 30.5274
.. ... ...
162 order=(3,1,0), season=(0,1,0) 35.6774
163 order=(3,1,0), season=(0,1,1) 26.6998
164 order=(3,1,0), season=(1,0,0) 36.7483
165 order=(3,1,0), season=(1,0,1) 37.3619
166 order=(3,1,0), season=(1,1,0) 27.1641
167 order=(3,1,0), season=(1,1,1) 23.5206
168 order=(3,1,1), season=(0,0,0) 46.0088
169 order=(3,1,1), season=(0,0,1) 42.0283
170 order=(3,1,1), season=(0,1,0) 33.2783
171 order=(3,1,1), season=(0,1,1) 23.3888
172 order=(3,1,1), season=(1,0,0) 33.2987
173 order=(3,1,1), season=(1,0,1) 34.8924
174 order=(3,1,1), season=(1,1,0) 24.7505
175 order=(3,1,1), season=(1,1,1) 25.6202
176 order=(3,1,2), season=(0,0,0) 40.3796
177 order=(3,1,2), season=(0,0,1) 37.4187
178 order=(3,1,2), season=(0,1,0) 35.7897
179 order=(3,1,2), season=(0,1,1) 23.3374
180 order=(3,1,2), season=(1,0,0) 38.7358
181 order=(3,1,2), season=(1,0,1) 37.6919
182 order=(3,1,2), season=(1,1,0) 29.2141
183 order=(3,1,2), season=(1,1,1) 27.3448
184 order=(3,1,3), season=(0,0,0) 41.1869
185 order=(3,1,3), season=(0,0,1) 34.1721
186 order=(3,1,3), season=(0,1,0) 34.8843
187 order=(3,1,3), season=(0,1,1) 23.1797
188 order=(3,1,3), season=(1,0,0) 40.3741
189 order=(3,1,3), season=(1,0,1) 35.8745
190 order=(3,1,3), season=(1,1,0) 23.1581
191 order=(3,1,3), season=(1,1,1) 29.1668
[192 rows x 2 columns]
model aic
59 order=(1,1,3), season=(0,1,1) 20.1616
「order=(1,1,3), season=(0,1,1)」が最適なパラメータらしいので、
このパラメータでSARIMAモデルを作成する。
p=1
d=1
q=3
sp=0
sd=1
sq=1
sarima = sm.tsa.SARIMAX(
ts, order=(p,d,q),
seasonal_order=(sp,sd,sq,4),
enforce_stationarity = False,
enforce_invertibility = False
).fit()
# 結果確認
print(sarima.summary())
Statespace Model Results
=========================================================================================
Dep. Variable: プライム No. Observations: 28
Model: SARIMAX(1, 1, 3)x(0, 1, 1, 4) Log Likelihood -4.081
Date: Sat, 26 Aug 2017 AIC 20.162
Time: 10:16:53 BIC 28.155
Sample: 04-01-2010 HQIC 22.605
- 01-01-2017
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
ar.L1 0.7597 2.03e+06 3.74e-07 1.000 -3.99e+06 3.99e+06
ma.L1 -1.2405 0.000 -5216.846 0.000 -1.241 -1.240
ma.L2 -0.0121 0.003 -4.468 0.000 -0.017 -0.007
ma.L3 0.2525 0.011 22.090 0.000 0.230 0.275
ma.S.L4 -1.0001 0.013 -77.808 0.000 -1.025 -0.975
sigma2 0.0624 0.015 4.218 0.000 0.033 0.091
===================================================================================
Ljung-Box (Q): 5.47 Jarque-Bera (JB): 0.47
Prob(Q): 0.98 Prob(JB): 0.79
Heteroskedasticity (H): 0.21 Skew: -0.43
Prob(H) (two-sided): 0.11 Kurtosis: 3.02
===================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
[2] Covariance matrix is singular or near-singular, with condition number 2.18e+36. Standard errors may be unstable.
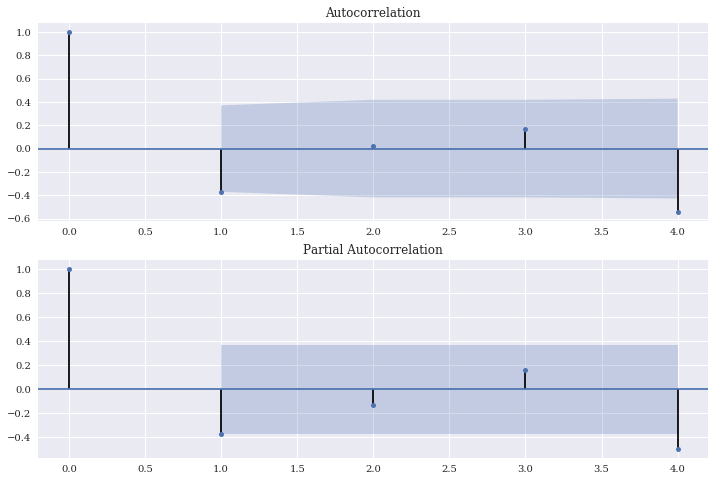
# 残差のチェック
residSARIMA = sarima.resid
fig = plt.figure(figsize=(12,8))
# 自己相関
ax1 = fig.add_subplot(211)
fig = sm.graphics.tsa.plot_acf(residSARIMA, lags=4, ax=ax1)
# 偏自己相関
ax2 = fig.add_subplot(212)
fig = sm.graphics.tsa.plot_pacf(residSARIMA, lags=4, ax=ax2)
残差の自己相関については、ほぼ問題なくなったことを確認。
最後に予測
長々と色々見てきましたが、SARIMA モデルでどれだけ予測できるのかを見てみます。
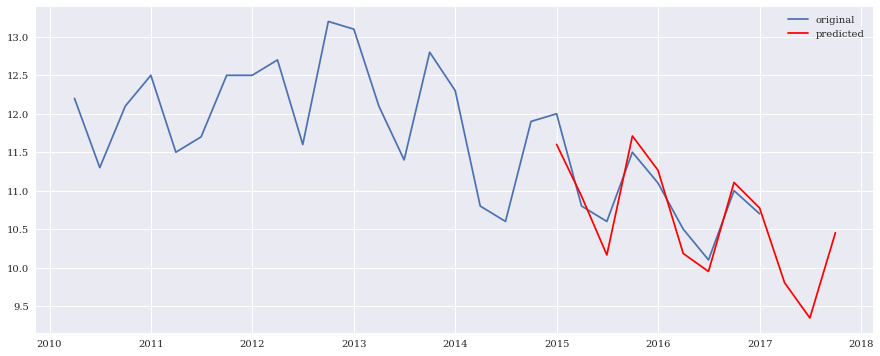
元データは2010年1Qから2016年4Qですが、この元データと予測データ(2015年1Q-2017年4Q)までを同時プロットしてみます。
# 予測
ts_pred = sarima.predict('2015-01-01', '2017-12-01')
# 実データと予測結果の図示
plt.plot(ts, label='original')
plt.plot(ts_pred, label='predicted', color='red')
plt.legend(loc='best')
print(ts_pred)
2015-01-01 11.601939
2015-04-01 10.927707
2015-07-01 10.164144
2015-10-01 11.711078
2016-01-01 11.266165
2016-04-01 10.183324
2016-07-01 9.949642
2016-10-01 11.106567
2017-01-01 10.775023
2017-04-01 9.803198
2017-07-01 9.344881
2017-10-01 10.452862
Freq: QS-OCT, dtype: float64
2015-2016年度のデータはまずまずの精度で予測できていることが分かります。
2017年度は秋口にかけて大きく下落し、冬に大きく上昇することが予測できそう。
トレンドを加味して予測するのはさほど難しくないですね。
今回はcost function による厳密なcost分析を行っていませんが、
今後のアンサンブル解析時の課題としたいと思います。
今回の解析notebook
今回の詳細データ解析過程については notebook を参照してください。
https://github.com/mshinoda88/python/blob/master/20170822-01_tvasahi.ipynb