こちらの勉強会は、本形式にまとめています。
https://zenn.dev/mandenaren/books/algorithm-study
はじめに
新卒エンジニア同士で実施している勉強会の第 6 回目~最終回の記事になります。
今回のテーマはグラフ理論についてです。
| 回 | テーマ |
|---|---|
| 第 1 回 | 二分探索 |
| 第 2 回 | ソートアルゴリズム |
| 第 3 回 | 暗号化 |
| 第 4 回 | bit 演算 |
| 第 5 回 | 連想配列 |
| 第 6 回 | グラフ理論 |
前提
グラフ理論とはネットワークや組織、経路のようなグラフ構造を扱うための学問です。
グラフ構造は、ノード(点)とエッジ(線)から成るデータ構造です。ある頂点に何本の線が繋がっているかを次数と言います。
古くからは数学的なアプローチによる研究が行われてきました。
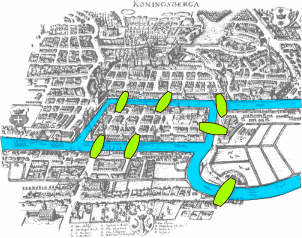
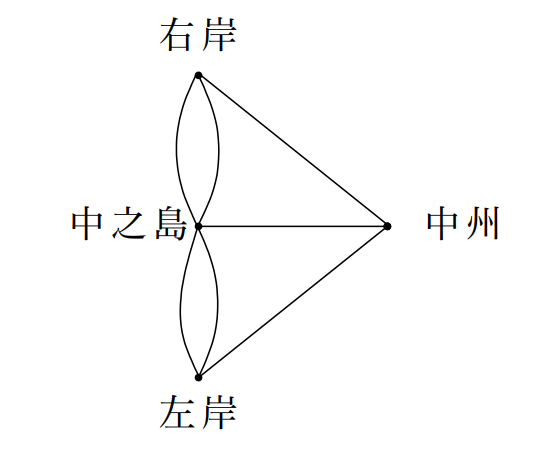
起源は、オイラーという数学者がケーニヒスベルクにかかる 7 つの橋を全て渡って元に戻ってこられるか、という問題を解くことから始まりました。これは一筆書きと同じ意味を指します。
結論としてこれらの橋は一筆書きできません。一筆書きができる条件は以下のように求められています。
- すべての頂点の次数が偶数
- 次数が奇数である頂点の数が 2 で、残りの頂点の次数は全て偶数
現代では、コンピュータリソースの発展により大規模なグラフ構造=ネットワークを計算できるようになってきました。世の中には、ネットワーク構造でモデル化できる事柄がたくさんあります。
- 路線図、乗り換え案内
- カーナビ、経路探索
- インターネット、検索
- SNS、フォロー
- ...
これらのネットワークを考察するにあたっては、グラフ構造をコンピュータが計算できるデータ構造として定義する必要があります。点と線、そしてそのつながりをどのように表現できるのかを見ていきましょう。
問題 1
M 頂点、N 辺の無向グラフが与えられます。無向とは線に向きが存在しないことを意味します。
自分自身より頂点番号が小さい隣接頂点がちょうど 1 つ存在する頂点の個数はいくつかを出力してください。
5 6 // M, N
1 2 // 頂点1と頂点2が線で結ばれている。以下同様。
1 3
3 2
5 2
4 2
4 5
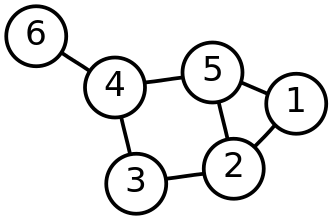
上記のテストケースは以下ように理解します。
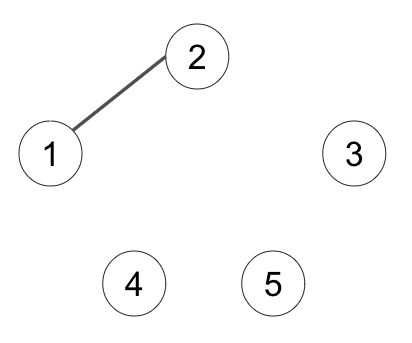
まず、頂点数が 5 なので 5 つの点を用意します。
線の数が 6 本あるので、6 行分の線の情報があります。2 行目は頂点 1 と頂点 2 が線で結ばれていることを表します。
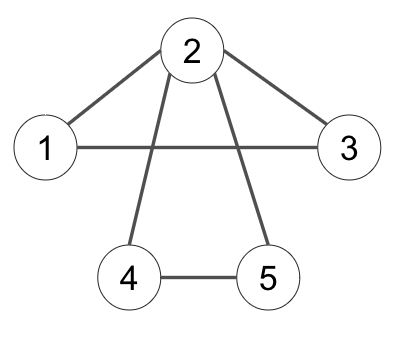
以下同様に 6 行分の線を書くと最終的に以下ようなグラフになります。
「自分自身より頂点番号が小さい隣接頂点がちょうど 1 つ存在する頂点の個数」を次のように数えます。
まず 1 の頂点に注目すると、自分より頂点番号が小さいものが存在しないので対象外です。
2 の頂点を見ると、繋がっている点として 1 があるので自分より頂点番号が小さい点が一つだけあることになり題意に当てはまります。
3 の頂点を見ると、1,2 と繋がっていて自分より小さい点 2 つと繋がっているので題意に当てはまりません。
4 の頂点を見ると、2,5 と繋がっていて自分より小さい点が一つだけあるので、題意に当てはまります。
5 の頂点を見ると、2,4 と繋がっていて自分より小さい点 2 つと繋がっているので題意に当てはまりません。
結果として題意を満たす頂点は 2,4 の 2 つなので回答は 2 となります。
なお、以下の条件に従ってください。
- テストケースは全て満たすこと
- 組み込みメソッドは使わないこと。つまり、分岐、繰り返し処理を自分で書くこと。
- Array.find などは使わない
- 解法を調べるために chatgpt、インターネットは使用しないこと
- 文法を調べることのみ可
- 計算量は問いません
テストケース
5 6
1 2
1 3
3 2
5 2
4 2
4 5
2
2 1
1 2
1
7 18
7 2
1 6
5 2
1 3
7 6
5 3
5 6
5 4
1 7
2 6
3 4
5 1
4 7
4 6
5 7
3 2
4 2
1 4
0
コマンドラインからの入力を受け取る方法
# 入力
# M頂点、N辺の数を受け取る
M, N = map(int, input().split())
# N辺分の頂点の結びを受け取る
for i in range(N):
a, b = map(int,input().split())
解答例
クリックすると解答例が見られます
グラフ構造の表現でよく用いられるデータ構造は隣接行列、隣接リストがあります。
隣接行列を用いた方法
# 入力
M, N = map(int, input().split())
# 隣接行列の初期化
adjacency_matrix = [[0 for _ in range(M)] for _ in range(M)]
for i in range(N):
a, b = map(int,input().split())
adjacency_matrix[a-1][b-1] = 1
adjacency_matrix[b-1][a-1] = 1
count = 0
for i in range(M):
smaller_neighbors = 0
for j in range(i):
if adjacency_matrix[i][j] == 1:
smaller_neighbors += 1
if smaller_neighbors == 1:
count += 1
print(count)
[
[0, 1, 1, 0, 0],
[1, 0, 1, 1, 1],
[1, 1, 0, 0, 0],
[0, 1, 0, 0, 1],
[0, 1, 0, 1, 0]
]
隣接行列はグラフ構造を二次元配列で表現し、繋がっているか否かを 0,1 で表します。例えば、1 行目の配列は頂点 1 が 2,3 と繋がっていることを表します。テストケースの隣接行列を作成したら、隣接行列を頂点ごとにループで回し、自分自身より小さい頂点を繋がっている線をカウントします。それがちょうど一つだけ存在する場合にカウントし、結果を出力します。
隣接リストを用いた方法
# 入力
M, N = map(int, input().split())
# 隣接リストの初期化
adjacency_list = [[] for _ in range(M)]
for i in range(N):
a, b = map(int,input().split())
adjacency_list[a-1].append(b)
adjacency_list[b-1].append(a)
count = 0
for i in range(M):
smaller_neighbors = 0
for j in adjacency_list[i]:
if j < i+1:
smaller_neighbors += 1
if smaller_neighbors == 1:
count += 1
print(count)
[[2, 3], [1, 3, 5, 4], [1, 2], [2, 5], [2, 4]]
隣接リストもグラフ構造を二次元配列で表現し、インデックスを頂点をみなして繋がっている頂点を配列として持ちます。例えば、1 つ目の要素=頂点 1 は、2,3 の頂点と繋がっていることを表します。テストケースの隣接リストを作成したら、隣接リストをループで回し、各頂点自分自身より小さい頂点を繋がっている線をカウントします。それがちょうど一つだけ存在する場合にカウントし、結果を出力します。
この問題でグラフ構造の 2 種類の表現方法を学びました。それぞれには特徴があります。計算量を考えると、隣接行列は O(N^2)、隣接リストは O(N+M)となるので隣接リストの方が効率的となります。しかし、隣接行列は情報量が多い分、できることの幅が広い表現形式です。例えば、線にコストが発生するような情報(電車の運賃など)を扱いたい場合、任意の数字を各マスに置くことで表現することができます。これを特に距離行列を言ったりします。また、行列形式なので色々な数学演算が可能となります。
問題 2
グラフ構造を応用して簡単なカーナビを作りましょう。
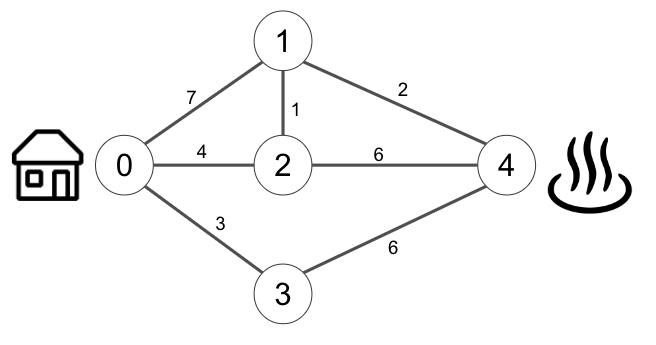
家から温泉まで行くには以下のような経路が存在します。
それぞれの線には距離が存在し、0 と 1 の距離は 7 となります。距離情報を踏まえて家から温泉までの最短経路を求めてください。
家から温泉までたどり着く経路には例えば 0→3→4 があり、距離は 9 です。しかし、0→2→1→4 の経路を辿る場合距離は 7 となり、実はこちらが最短経路となります。
なお、入力形式は以下とします。M 頂点、N 辺の重み付き無向グラフが与えられます。
始点 S から終点 E までの最短経路を求めます。
5 7 0 4 // M, N, S, E
0 1 7 // 頂点0と頂点1が距離7の線で結ばれている。以下同様。
0 2 4
0 3 3
1 2 1
1 4 2
2 4 6
3 4 6
なお、以下の条件に従ってください。
- テストケースは全て満たすこと
- 組み込みメソッドは使わないこと。つまり、分岐、繰り返し処理を自分で書くこと。
- Array.find などは使わない
- 解法を調べるために chatgpt、インターネットは使用しないこと
- 文法を調べることのみ可
- 計算量は問いません
5 7 0 4
0 1 7
0 2 4
0 3 3
1 2 1
1 4 2
2 4 6
3 4 6
[0, 2, 1, 4]
7
4 3 0 3
0 1 3
1 2 4
2 3 5
[0, 1, 2, 3]
12
6 9 0 5
0 1 3
0 2 2
1 2 1
1 3 2
2 3 3
2 4 2
3 5 1
4 5 2
1 4 3
[0, 2, 4, 5]
6
コマンドラインからの入力を受け取る方法
# 入力
M, N, S, E = map(int, input().split())
# N辺分の頂点の結びと距離を受け取る
for i in range(N):
a, b, c = map(int,input().split())
解答例
クリックすると解答例が見られます
# 入力
M, N, S, E = map(int, input().split())
# 隣接行列の初期化
INF = float('inf')
adjacency_matrix = [[INF for _ in range(M)] for _ in range(M)]
# 距離行列の作成
for i in range(M):
adjacency_matrix[i][i] = 0
for i in range(N):
a, b, c = map(int,input().split())
adjacency_matrix[a][b] = c
adjacency_matrix[b][a] = c
# ダイクストラ法
def dijkstra(S, E, adjacency_matrix):
INF = float('inf')
dist = [INF] * M
prev = [None] * M
visited = [False] * M
dist[S] = 0
for _ in range(M):
min_dist = INF
for v in range(M):
if not visited[v] and dist[v] < min_dist:
min_dist = dist[v]
current_minimum_node = v
visited[current_minimum_node] = True
for neighbor in range(M):
if not visited[neighbor] and dist[current_minimum_node] + adjacency_matrix[current_minimum_node][neighbor] < dist[neighbor]:
dist[neighbor] = dist[current_minimum_node] + adjacency_matrix[current_minimum_node][neighbor]
prev[neighbor] = current_minimum_node
path = [E]
while path[-1] != S:
path.append(prev[path[-1]])
path = path[::-1]
return path, dist[E]
path, min_dist = dijkstra(S, E, adjacency_matrix)
print(path)
print(min_dist)
最短経路問題を解くにあたって、ダイクストラ法として知られるアルゴリズムを実装します。まず、距離行列を作成します。
[
[0, 7, 4, 3, inf],
[7, 0, 1, inf, 2],
[4, 1, 0, inf, 6],
[3, inf, inf, 0, 5],
[inf, 2, 6, 5, 0]
]
1 行目では頂点 1 が 2,3,4 にそれぞれの距離で繋がっていることを表します。また、自分自身との間の距離は 0, 直接移動できない頂点同士の距離は無限大として置きます。
そして、指定のグラフ(距離行列)に関して、始点から終点までの最短距離をダイクストラ法で解きます。
ダイクストラ法は以下のようなアルゴリズムとなります。
まず変数に関して、
visited: 訪れた頂点
prev: 各頂点に最短経路で到達する前のノードを格納する配列
dist: 各頂点に到達する最短距離を格納する配列
のように定義します。
メインループの中で以下の処理を行います。
- 未訪問の頂点の中で最短距離が最小となる点を見つけて、visited を更新する。
- 上記の点に隣接している未訪問の頂点のうち、距離が現在の
distより小さい場合、dist と prev を更新する。
具体的な値を見ていきましょう。まず、初期状態では、
visited: [False, False, False, False, False]
prev: [None, None, None, None, None]
dist: [0, inf, inf, inf, inf]
このようになります。
ループ 1 では、未訪問の最短距離が最小となる頂点は 0 が選ばれます。0 に隣接している未訪問の頂点 1,2,3 への距離は、いずれも現在のdistより小さいので更新されます。
visited: [True, False, False, False, False]
prev: [None, 0, 0, 0, None]
dist: [0, 7, 4, 3, inf]
ループ 2 では、未訪問の最短距離が最小となる頂点は 3 が選ばれます。3 に隣接している未訪問の頂点 4 への距離は、現在のdist[4]より小さいので更新されます。
visited: [True, False, False, True, False]
prev: [None, 0, 0, 0, 3]
dist: [0, 7, 4, 3, 9]
ループ 3 では、未訪問の最短距離が最小となる頂点は 2 が選ばれます。2 に隣接している未訪問の頂点は 1,4 があり、1 の場合のみ現在のdist[1]より小さいので更新されます。
visited: [True, False, True, True, False]
prev: [None, 2, 0, 0, 3]
dist: [0, 5, 4, 3, 9]
ループ 4 では、未訪問の最短距離が最小となる頂点は 1 が選ばれます。1 に隣接している未訪問の頂点は 4 があり、現在のdist[1]より小さいので更新されます。
visited: [True, True, True, True, False]
prev: [None, 2, 0, 0, 1]
dist: [0, 5, 4, 3, 7]
ループ 5 では、未訪問の最短距離が最小となる頂点は 4 が選ばれます。4 に隣接している未訪問の頂点はないので更新されません。
visited: [True, True, True, True, True]
prev: [None, 2, 0, 0, 1]
dist: [0, 5, 4, 3, 7]
これで全ての点が訪問済みとなりループは終了します。最終的なdistは始点から各頂点への最短距離を、prevは各頂点に最短経路で到達する前のノードを表します。
最短経路を求める際は、終点から辿っていきます。まず、終点 4 の前のノードはprev[4]: 1 となります。頂点 1 の前のノードはprev[1]: 2 となります。頂点 2 の前のノードはprev[2]: 0 となります。つまり、4←1←2←0 のように最短経路が選ばれたということになります。
おわりに
勉強会第 6 回~最終回の内容として、グラフ理論をテーマに学びました。グラフ理論は、ノードやエッジで構成されるグラフ構造を数学的、計算機科学的なアプローチで研究していく学問です。コンピュータでグラフ構造を扱う場合は、隣接行列や隣接リストといった表現形式を使用し、計算ができるようになります。
グラフ構造は、普段我々の生活の中においても、カーナビ、乗換案内、インターネット検索、SNS など様々な事柄をモデル化できます。
関わる業界によっては、対象ドメインをグラフ構造でモデル化することを検討できるかもしれません。
最後に、勉強会の締めとして、、、
全六回分のテーマと問題演習を通して、現象をコンピュータでどのように表現できるのか?アルゴリズムがどのように現代技術を支えているのか?の一端を体験できたのではないかなと思います。普段当たり前のように活用している技術はこういった背景で成り立っているのか!が理解できてくれば、普段の業務に納得感が得られ、より楽しくエンジニアリングに向き合えるようになるでしょう。こちらの勉強会がお役に立てれば幸いです!