SPSS Statisticsによる生存分析④時間依存のCox回帰

SPSS Statisticsによる生存分析①生命表
SPSS Statisticsによる生存分析②Kaplan-Meier
SPSS Statisticsによる生存分析③Cox回帰
SPSS Statisticsによる生存分析④時間依存のCox回帰

はじめに

■環境
Windows 10
SPSS Statistics 28.0.1
SPSS Advanced Statisticsオプション

■データ
https://github.com/Makimaki2020/sampledata/blob/main/Survival.sav?raw=true
このデータには、患者238人のケガの治療法(治療法A、治療法B)、薬の投与量、健康状態(良い、悪い)、治療完了までの日数と状況(治療完了、打ち切り)があります。

SPSS Statisticsの生存分析

生存分析とは、ある事象(イベント)が起こるまでの時間の長さに対する分析です。たとえば、患者の治療時間や生存期間、登録会員が退会するまでの期間、機械、システム、製品、部品の故障までの時間や寿命の長さ、またローン審査にかかる時間など分析することができます。これらのデータの特徴は時間の経過に伴い分析の対象が減少していく点にあります。患者の治療時間を扱う場合、治療完了のステータスになるとその患者のデータはその時点から対象から除かれます。また、何らかの事情で途中で治療を取りやめてしまった場合にもその患者のデータはその時点から対象から除かれます。このような「打ち切り」を含むデータを生存分析では扱うことができます。

生存分析分析のメニューは次の通りです。

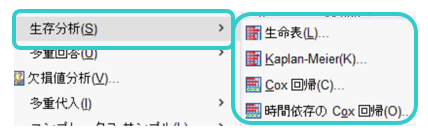
それぞれのメニューの主な目的と概要です。

時間依存のCox回帰

ここでは、時間依存のCox回帰を取り上げます。
このメニューの主な目的は、時間に依存する共変量を含む共変量に基づいて、事象までの時間をモデル化することです。
手順は、[分析]メニュー＞[生存分析]＞[時間依存のCox回帰]を選択します。
[時間依存の共変量の計算]ダイアログで、式を入力します。
ここでは、治療を開始してから365日(約１年)以降から治療法によるハザード比が一定でなくなっています。
Cox回帰メニューで作成したログマイナスログのグラフ

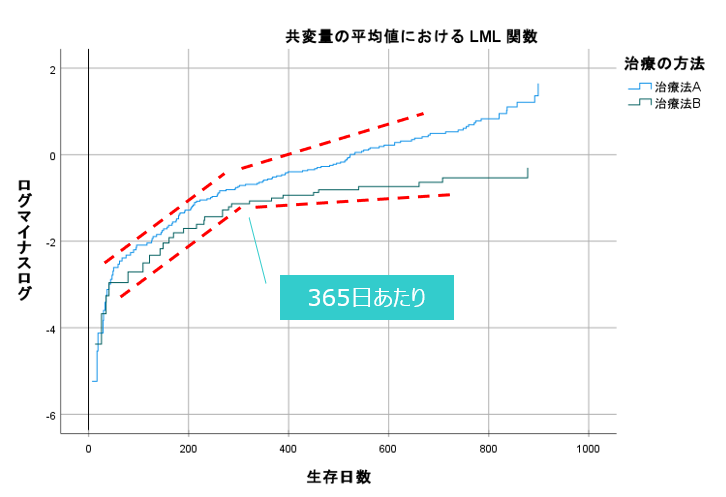
時間変数[T_]が365よりも大きい場合を真(１)、そうでない(365以下の)場合を偽(０)として、治療法を乗じます。
T_COV_は時間と治療法の交互作用です。時間は、(生存時間＞365)＝１、(生存時間＜＝365)＝０です。治療方法は、治療法A＝０、治療法B＝１です。T_COV_＝０は、❶(生存時間＜＝365)×治療法A、❷(生存時間＜＝365)×治療法B、❸(生存時間＞365)×治療法A、T_COV_＝１は、❹(生存時間＞365)×治療法Bで、T_COV_は❶から❹までの４種類で❶、❷、❸は０、❹は１です。

時間依存の共変量の計算に関しては、こちらもご覧ください。
https://www.ibm.com/docs/ja/spss-statistics/28.0.0?topic=statistics-computing-time-dependent-covariates

これにより時間と治療法の交互作用の項ができることになります。

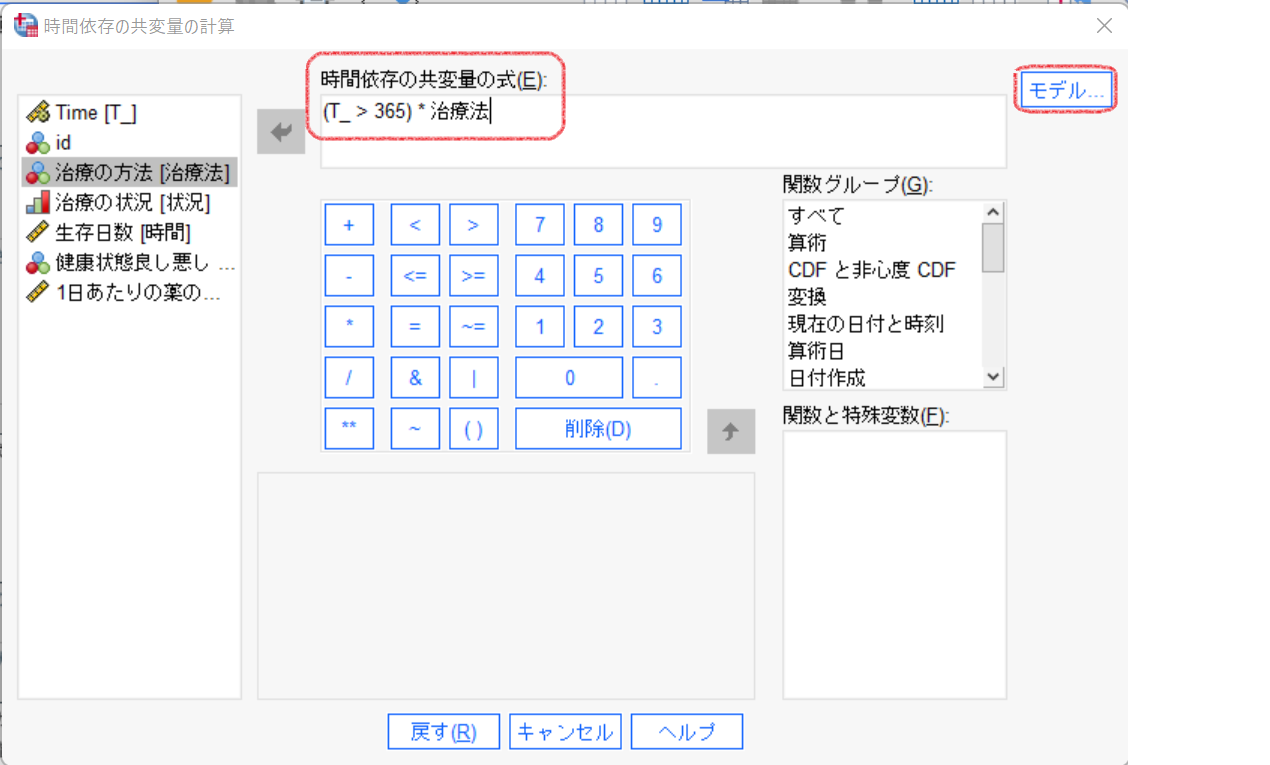
[モデル]ボタンをクリックします。

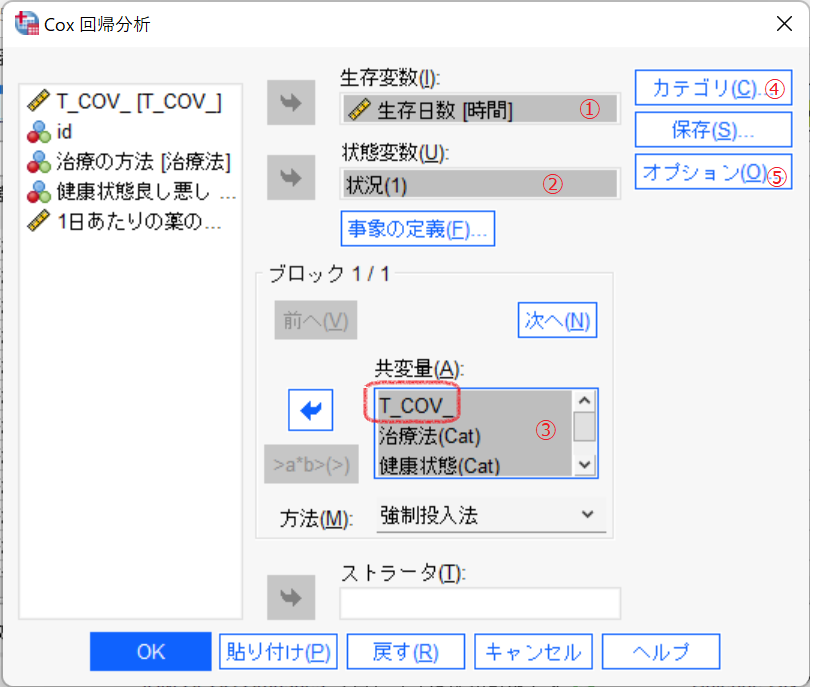
　①　時間変数を[生存変数]に指定します。
　②　状況や状態などを表す変数を[状態変数]に指定し、[事象の定義]で[状態変数]の事象(イベント)を表すコードを指定します。
　③　[ブロック]に共変量として説明変数を指定します。このとき、時間依存の共変量変数[T_COV_]も指定します。
　④　[カテゴリ]ボタンをクリックして、カテゴリ型の共変量を指定します。
　⑤　[オプション]ボタンをクリックして、[モデル統計量]の[expに関するCI]を選択します。

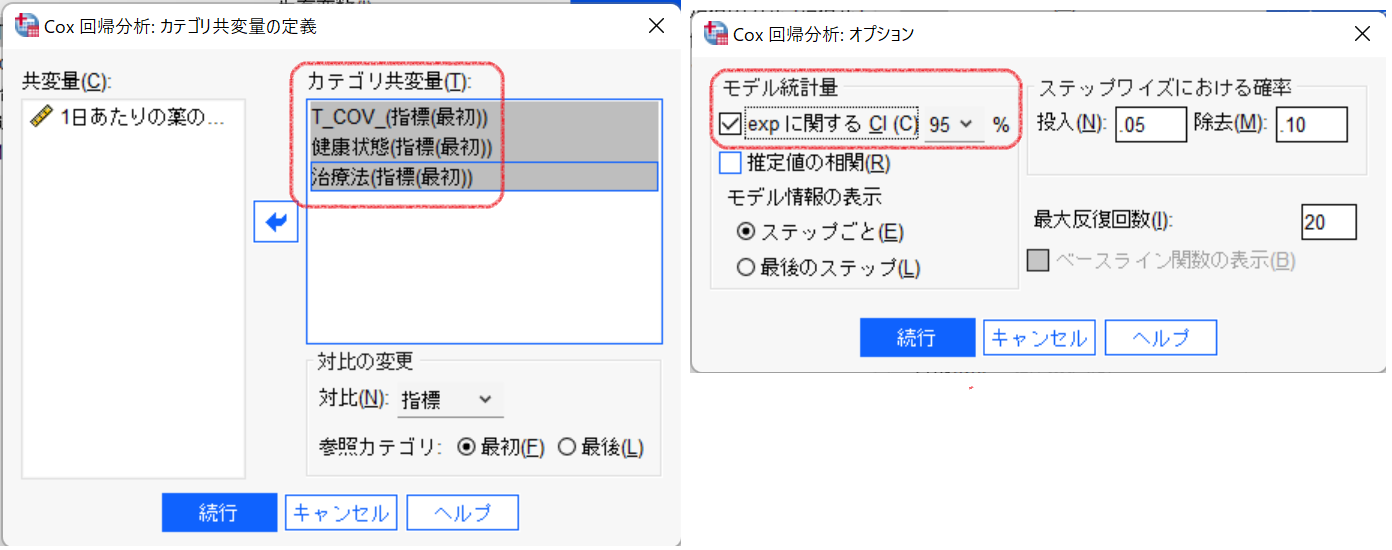
実行結果を見てみましょう。
カテゴリ変数のコーディングを確認しておきます。

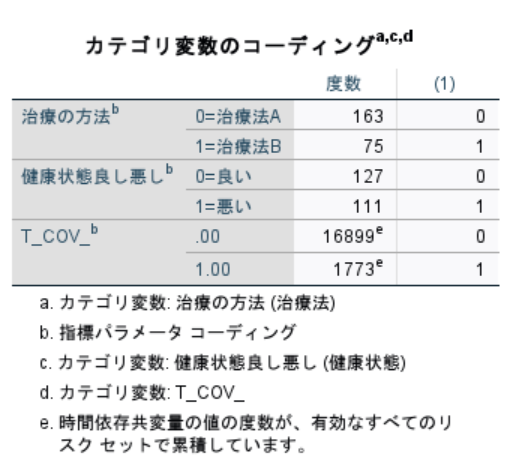
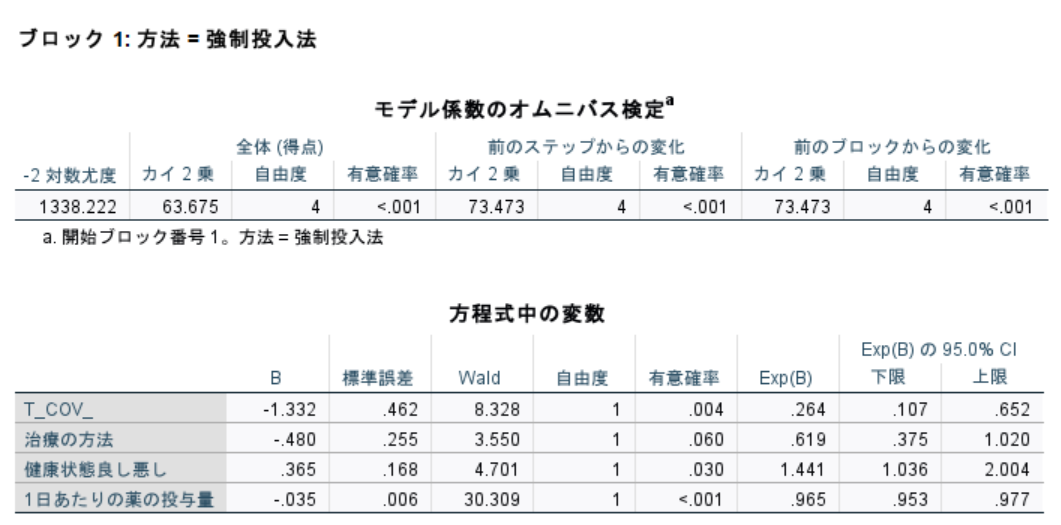
T_COV_以外の条件は同じで、T_COV_が０から1に代わるとハザード比であるExp(B)は0.264です。つまり、365日以降の治療方法Bは治療の効果が下がることになります。

まとめ

SPSS Statistics生存分析の時間依存のCox回帰の主な機能を紹介しました。

参考