SPSS Statisticsによる生存分析①生命表
SPSS Statisticsによる生存分析②Kaplan-Meier
SPSS Statisticsによる生存分析③Cox回帰
SPSS Statisticsによる生存分析④時間依存のCox回帰
はじめに
■環境
Windows 10
SPSS Statistics 28.0.1
SPSS Advanced Statisticsオプション
■データ
https://github.com/Makimaki2020/sampledata/blob/main/Survival.sav?raw=true
このデータには、患者238人のケガの治療法(治療法A、治療法B)、薬の投与量、健康状態(良い、悪い)、治療完了までの日数と状況(治療完了、打ち切り)があります。
SPSS Statisticsの生存分析
生存分析とは、ある事象(イベント)が起こるまでの時間の長さに対する分析です。たとえば、患者の治療時間や生存期間、登録会員が退会するまでの期間、機械、システム、製品、部品の故障までの時間や寿命の長さ、またローン審査にかかる時間など分析することができます。これらのデータの特徴は時間の経過に伴い分析の対象が減少していく点にあります。患者の治療時間を扱う場合、治療完了のステータスになるとその患者のデータはその時点から対象から除かれます。また、何らかの事情で途中で治療を取りやめてしまった場合にもその患者のデータはその時点から対象から除かれます。このような「打ち切り」を含むデータを生存分析では扱うことができます。
生存分析分析のメニューは次の通りです。
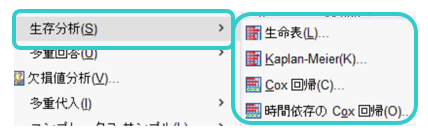
それぞれのメニューの主な目的と概要です。
Cox回帰
ここでは、Cox回帰を取り上げます。
このメニューの主な目的は、共変量(説明、もしくは独立変数)に基づいて、事象までの時間をモデル化することです。
手順は、[分析]メニュー>[生存分析]>[Cox回帰]を選択します。

① 時間変数を[生存変数]に指定します。
② 状況や状態などを表す変数を[状態変数]に指定し、[事象の定義]で[状態変数]の事象(イベント)を表すコードを指定します。
③ [ブロック]に共変量として説明変数を指定します。
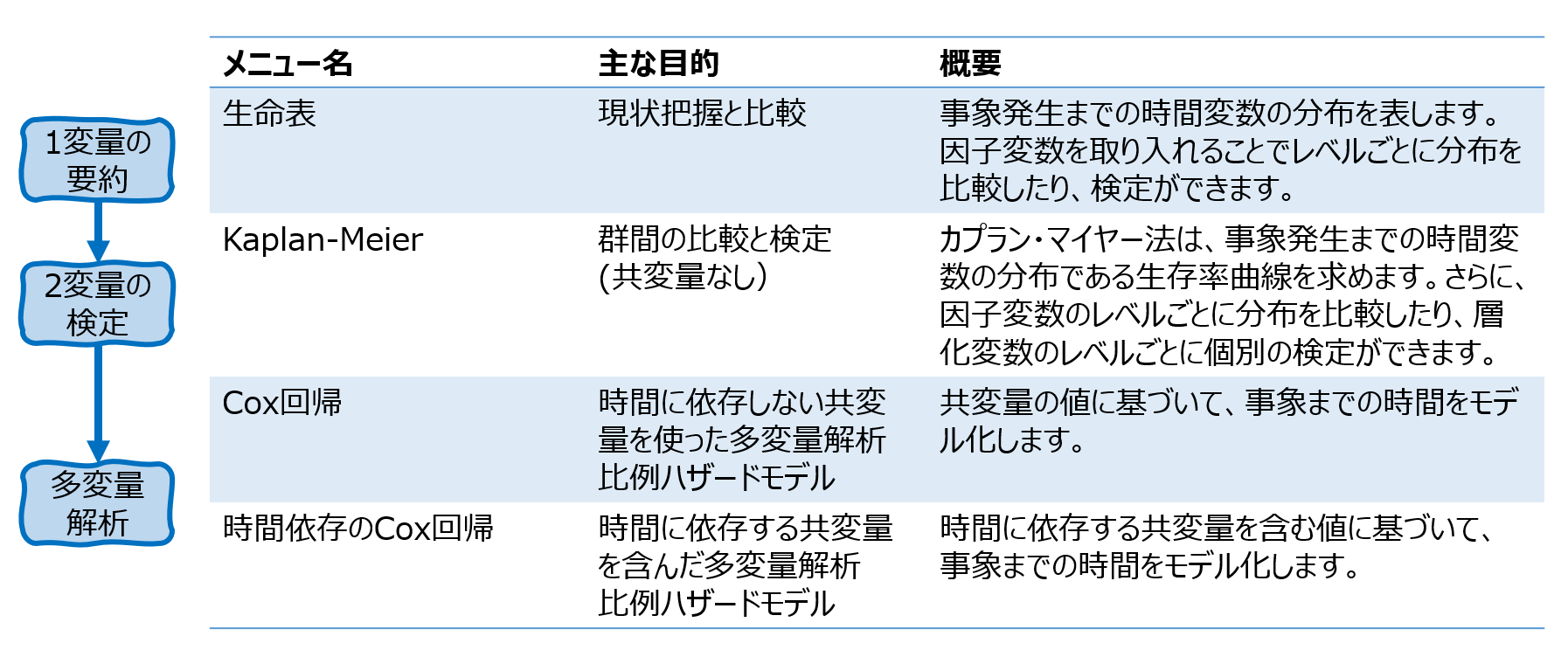
④ 共変量がカテゴリ型の場合には、[カテゴリ]ボタンをクリックして、その変数を[カテゴリ共変量]として指定します。
⑤ [作図]ボタンをクリックして、[作図の種類]の[累積生存率]を選択し、作図で表したい共変量を[個別の線]に指定します。
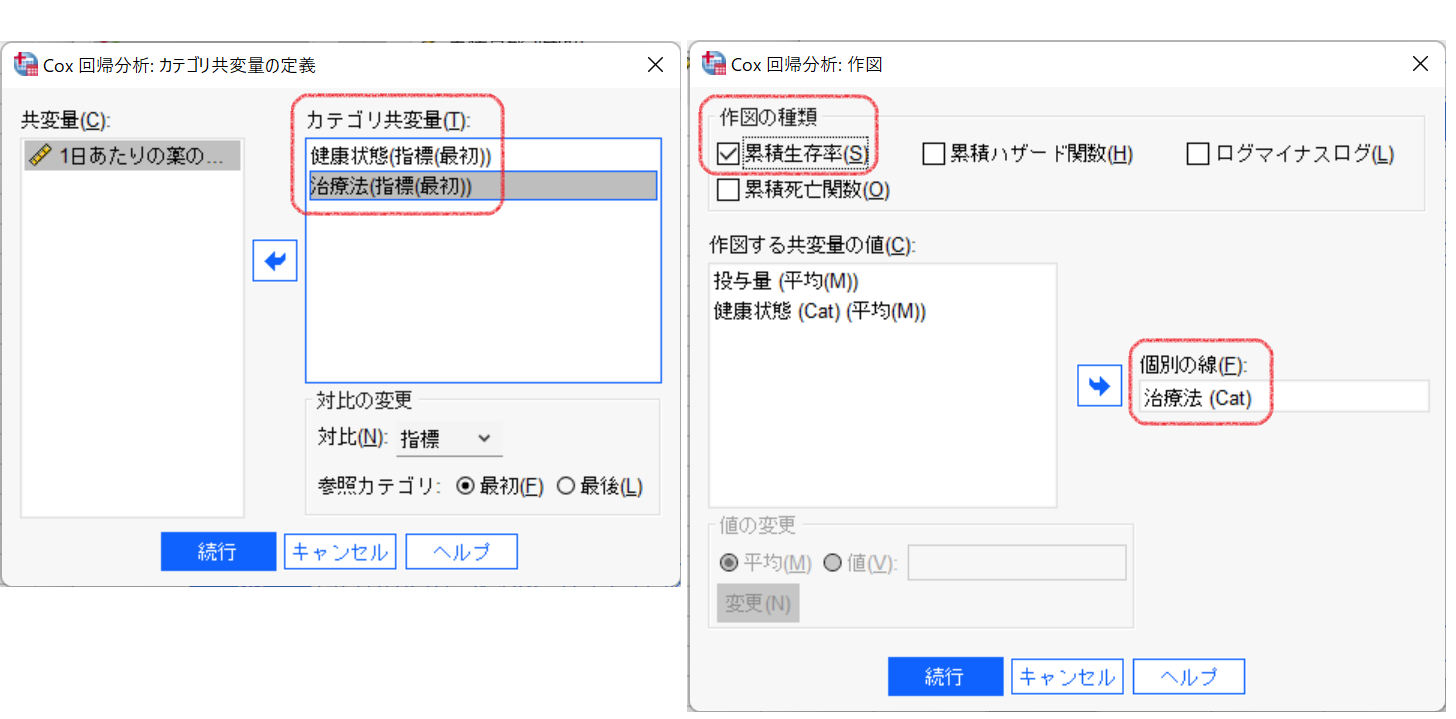
実行すると、まず使用したデータの要約が表示されます。
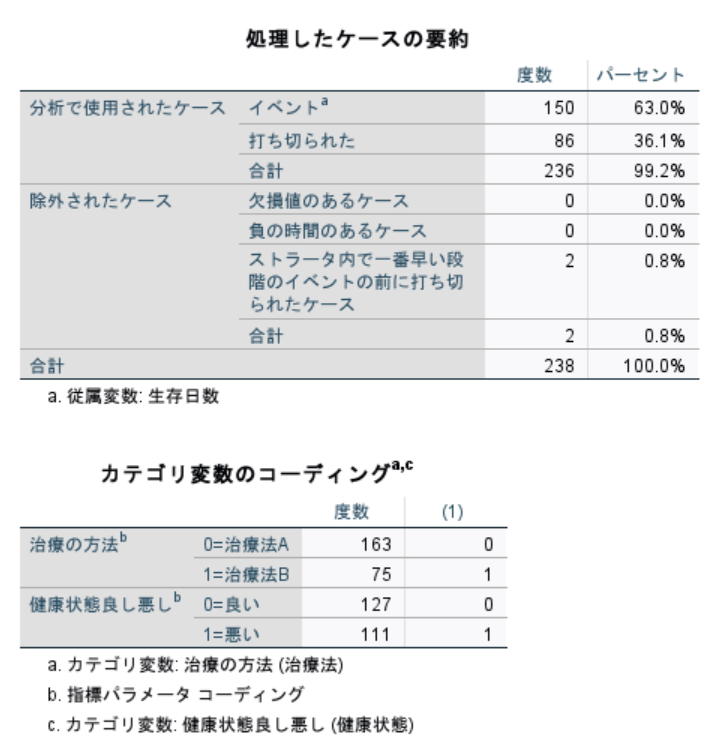
次にモデルの評価が表示されます。[モデル係数のオムニバス検定]では、モデル式の有意性を評価します。[全体(得点)]の有意確率からこのモデルが統計的に有意であることが示されています。[方程式中の変数]では、各共変量(説明変数)の有意性を有意確率で評価します。
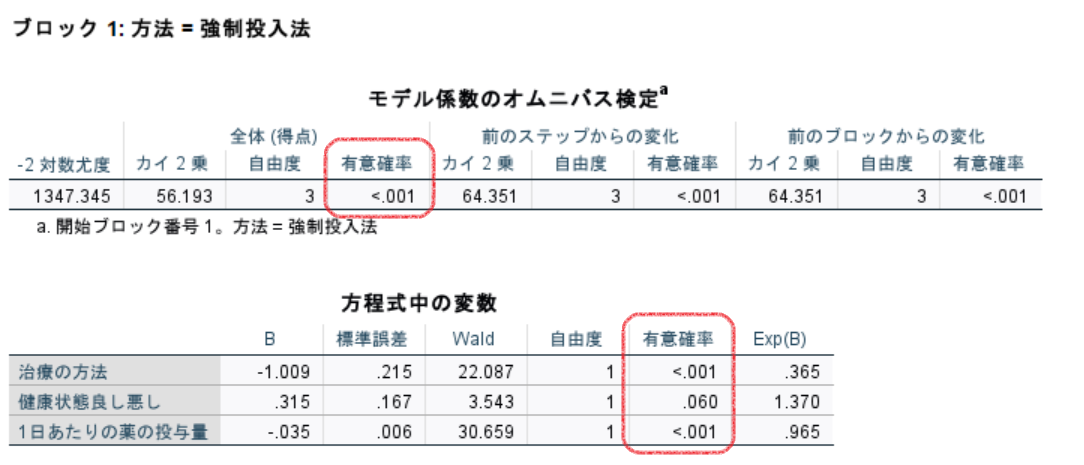
最後に累積生存率は全体とカテゴリ別の2種類が表示されます。治療法別のグラフからは、治療法Aの方が治療法Bより早い治療効果があることが読み取れます。
■全体
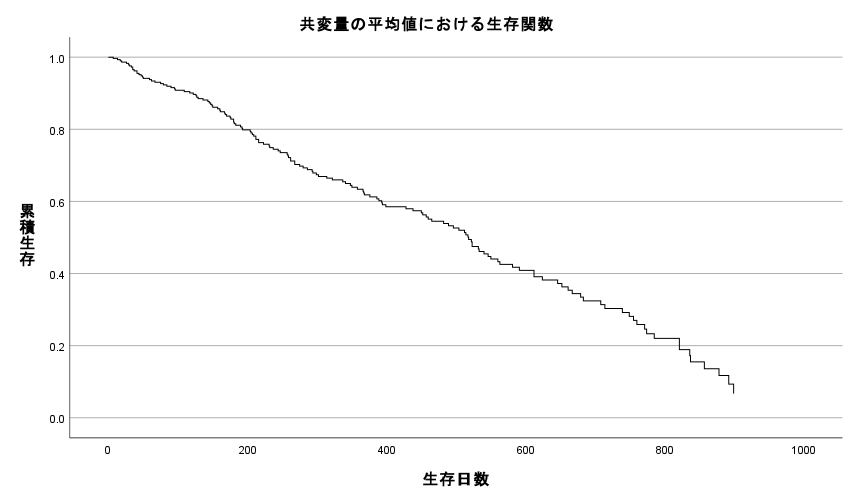
■治療法別

ここまでの分析から治療方法は、統計的にも治療完了までの時間に影響していて、治療法Aは治療法Bより効果があると言えそうです。
Cox回帰(比例ハザードモデル)の仮定
Cox回帰には、比例ハザード性(時間tによらずハザード比が一定)の仮定があります。この比例ハザード性の仮定を満たしているかどうかの確認方法はいくつかありますがここでは、Cox回帰メニューにあるグラフを使って確認してみます。
再度、Cox回帰のダイアログを表示します。
手順は、[分析]メニュー>[生存分析]>[Cox回帰]を選択します。
比例ハザード性を検証する共変量を[ブロック]から左の変数リストへ戻し、[ストラータ]に指定します。[作図]ボタンをクリックします。
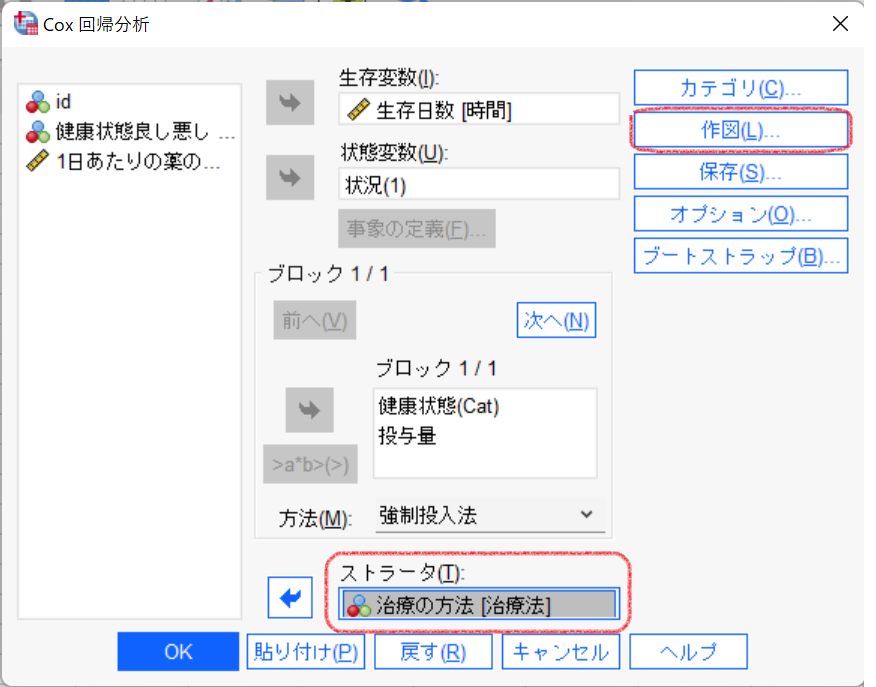
[作図の種類]で、「ログマイナスログ]を選択します。
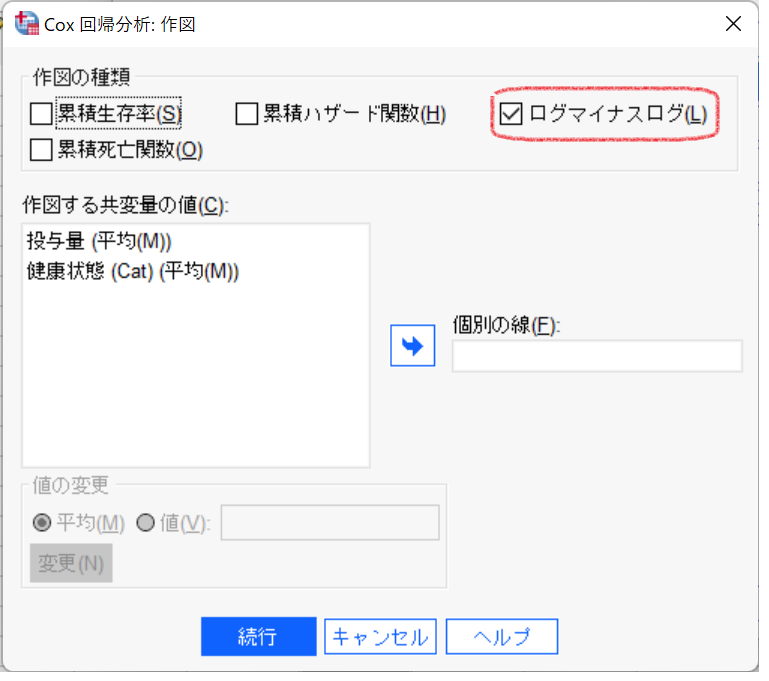
出力結果のグラフを参照します。赤い点線は後から描き入れたものです。時間が早い段階では、治療A・Bのハザードは平行ですが、途中から平行ではなくなっています。つまり、時間に依存することが伺えます。
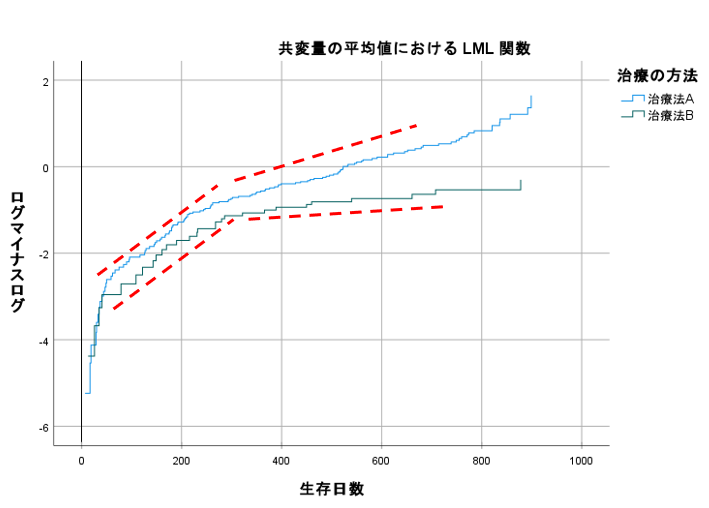
時間に依存する共変量がある場合には、分析の仮定を満たしていないことから時間依存のCox回帰を実行する必要があります。
まとめ
SPSS Statistics生存分析のCox回帰の主な機能を紹介しました。
参考