今回はせっかくqiitaも投稿始めたので、数ヶ月前に苦労して実装したpythonによる連続隠れマルコフモデルの実装について書こうと思います。
備忘録として自分が勉強した順に基本から書いていこうと思います。
また、この結果はおそらくできているだろうと思っていますが、動作怪しい部分もあるのでもし何かお気付きの方は教えていただけると幸いです。
マルコフモデルとは#
マルコフモデルとはマルコフ過程に基づいて作られるモデルのことで、マルコフ過程とはマルコフ性を持つ確率過程のことです。
マルコフたくさん出てきてなかなか理解できなかったので自分なりの理解を説明してみます。
まず以下のようなグラフ理論のような図を考えてみます。
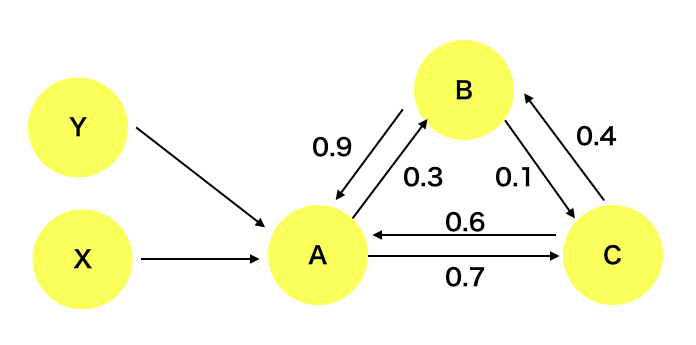
この図ではある一定時間後に矢印が向いている方向に状態が確率的に遷移し、その確率は矢印に添えられている数字だとします。
今状態Aだとすると0.3の確率で状態Bへ、0.7の確率で状態Cに遷移します。
もしA状態にXからきてもYからきても状態Aから状態Bまたは状態Cへの遷移確率は変わりません。
つまり、次の状態(BまたはC)への遷移確率は今の状態(A)のみに依存しているような性質をマルコフ性というとのことです。
確率過程とは、"時間とともに変化する確率変数のことである。-wikipedia-"と書いてありこの場合は状態を取る確率が時間によって変わるために確率過程と言えると考えています。すみません厳密な定義は他の情報サイトに譲ります
このような考え方で作られるモデルがマルコフモデルと言えます。
隠れマルコフモデル#
隠れマルコフモデルとは先ほどのマルコフモデルのようなモデルですが状態がわからない代わりに状態に依存したある値(出力)を持っている時に使われるモデルです。
自然言語処理を元に具体的に例を作ってみます。
まず、”I book a film”(私は映画を予約する)という例文(出力)を考える。この時”I"、"film"は名詞、"book"は動詞、"a"は冠詞である。このような品詞はこの文章からはわからないため隠れ状態と考えられます。
この文の品詞を機械に決めさせたいとします。しかし"I"や"a"はほぼ一意に決まるが"book"や"film"は名詞である本や映画を撮るといいた動詞の使い方もできます。そこで隠れマルコフモデルを用いてうまく品詞分類できないか考えてみます。
英文は5文型等ある程度品詞の順番が決まっています。そのため品詞の移り変わりのしやすさは以下の表のようになりそうです。(自分の感覚で値決めています)
| 文頭 | 名詞 | 動詞 | 冠詞 | 文末 | |
|---|---|---|---|---|---|
| 文頭 | 0 | 0.6 | 0.2 | 0.2 | 0 |
| 名詞 | 0 | 0.3 | 0.5 | 0.1 | 0.1 |
| 動詞 | 0 | 0.6 | 0 | 0.3 | 0.1 |
| 冠詞 | 0 | 1 | 0 | 0 | 0 |
| 文末 | 0 | 0 | 0 | 0 | 0 |
左が今の状態上が次の状態を示していると考えてください。一つ例をあげると名詞の次に名詞がくる確率は0.3、動詞が来る確率は0.5、冠詞が来る確率は0.1、文末が来る確率は0.1のような感じで見てください。確率に0を使うのはゼロ頻度問題的によくないのですが
そして各状態の時次のような確率で出力をとるとする。
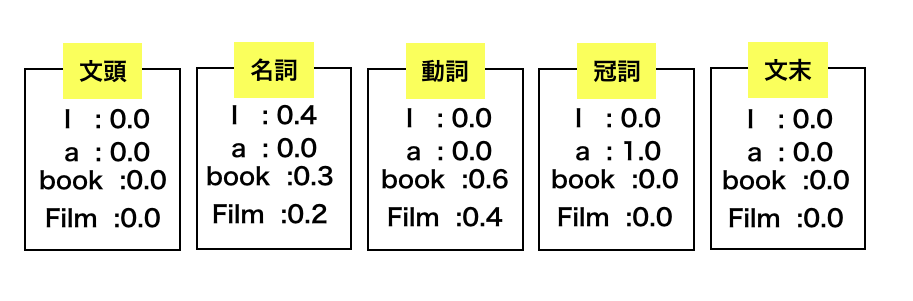
つまり名詞の時は"I"を0.4、"a"を0.0、"book"を0.3、"film"を0.2の確率でとるということです。
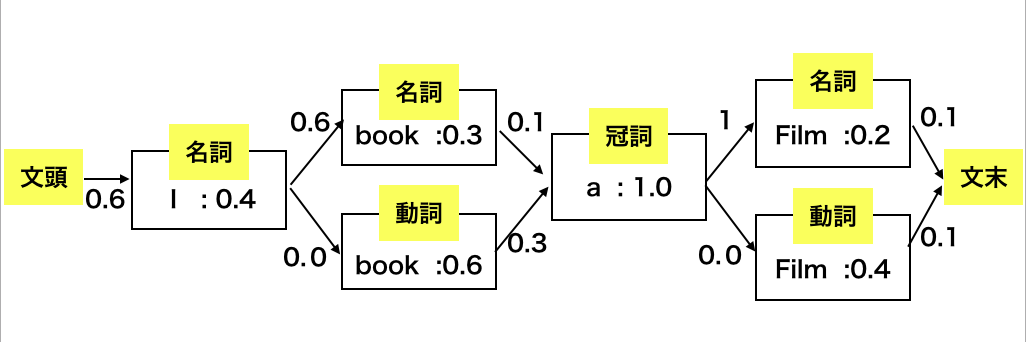
この時の状態遷移の仕方は次のようになります。(遷移確率が0の状態はあらかじめ削っています)
そして、単語数がn個、単語列(観測可能なもの)を$W=w_1,w_2,...,w_n$とし、品詞列(観測できないもの:状態)を$T=t_1,t_2,...,t_n$とするとある一つのルートを決めた時のこのモデルが出す確率は
$P(w)= \prod_{i=1}^{n}P(t_i|t_{i-1})P(w_i|t_i)$
で表すことができる。つまり前の状態から今の状態へと変わる確率$P(t_i|t_{i-1})$である遷移確率とある品詞の状態の時にその単語を出力する確率$P(w_i|t_i)$である出現確率の積を総乗することで求めることができる。
今回のモデルでは最初の状態(初期状態)は文頭でした。今回は最初の状態が文頭であることは自明であるが、他のデータに適応する時は最初の状態がどの状態から始まりやすいか(初期確率)も確率に大きく関わって来る。
そのため、このモデルが結果として出す確率は初期確率を$\pi_i$、遷移確率を$a_{i,j}$、出力関数を$b_j(w_t)$(ただしi,jはある状態を表し、tは出力の順番を示す。)と置き、状態の順番が$I=i_1,i_2,...,i_n$の時の確率は
$P(w)=\pi_{i_0}\prod_{t=1}^{n}a_{i_{t-1},i_t}b_{i_t}(w_t)$
(ただし、今回使用した文章の例だと$w_0$は空白、$w_1$は'I',...,$w_n$は空白のようになります。)
そしてこの確率がもっとも高い遷移の仕方を求めるとこの文の品詞を予測することができる。
ちなみにこの例の場合はわかりやすく偏らせたためと言えるが文頭→名詞→動詞→冠詞→名詞→文末といった順番で遷移する確率がもっとも高くなり、正しく品詞分類できていると考えられます。
余談ーーー
これからも初期確率は$\pi$
、遷移確率は$a_{i,j}$、出現確率は$b_j(w)$のような書き方で進めていきます。
ーーーーー
連続隠れマルコフモデル#
先ほどの隠れマルコフモデルは4つの単語について考えていたため出力は4値の出力として考えることができる。そのため出力は離散した値でした。そのため離散隠れマルコフモデルと言えます。
そのため気温のような連続した値を用いる場合の隠れマルコフモデルを連続隠れマルコフモデルというようです。
先ほどの離散マルコフモデルでは各状態の出現確率をそれぞれに求めていくが、連続値に対して全て値を振ることは現実的ではないので、混合ガウス分布を用いて出現確率を定義していきます。
連続隠れマルコフモデルの実装に入る前にまず混合ガウス分布について書いていこうと思います。
ガウス分布・混合ガウス分布#
混合ガウス分布とはガウス分布をいくつも足し合わせて確率分布を表現したものです。
そもそもガウス分布とは正規分布とも言われるもので、
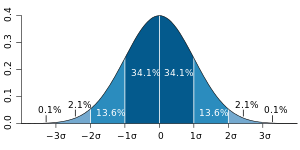
$N(x| \mu,\sigma)=\frac{1}{\sqrt{2 \pi\sigma^2}}\exp(-\frac{(x-\mu)^2}{2\sigma^2})$
-画像はwikipediaより拝借しました-
このグラフからわかるようにこのxが平均$\mu$(この図では0)に近いほど大きな値を取ることがわかります。そして分散が大きければ平べったい形になります。つまり、この値を確率と考えればxの値が平均$\mu$に近ければ近いほど高い値を取り、分散が大きければ平均から離れていてもその値をとる可能性はありうるようになると言えます。
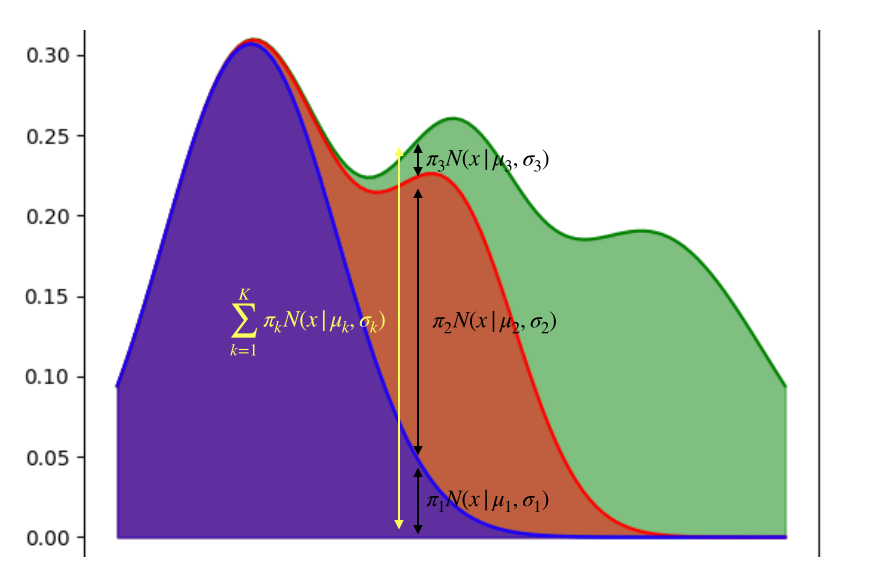
また混合ガウス分布はこの正規分布を複数足し合わせたようなもので、もしK個のガウス分布を合わせた混合ガウス分布の式は
$P(x|\pi,\mu,\sigma)=\sum_{k=1}^{K}\pi_kN(x|\mu_k,\sigma_k)$
ただし、$\sum_{k=1}^K\pi_k=1$の条件があります。
このようになります。
混合ガウス分布によるクラスタリング#
今後連続隠れマルコフモデルを実装するにあたってデータ点からガウス分布を特定する必要があります。そこで混合ガウス分布によるソフトクラスタリングの実装を行うことでその流れを見ていこうと思います。
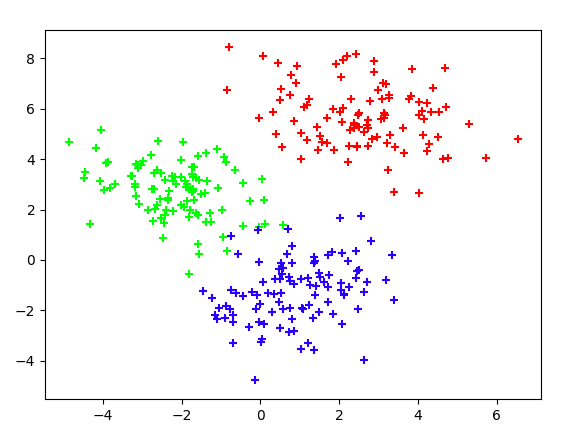
これがそのプロットになります。これらの点はどのガウス分布から生成されたのかわかっている状態です。(完全データ)
しかし、実際にクラスタリングするときはどの分布から生成されたのかわかりません。(不完全データ)
そのため、今からガウス分布に従ってもっともよく3つにわけられるように3つのガウス分布からなる混合ガウス分布のパラメータを調整していきます。
どのようにしたらうまく3つに分けることができるのか、それは求める混合ガウス分布による全ての点の同時確率がもっとも高くなれば良いということになります。つまり
$ln(p(X|\pi,\mu,\sigma))= ln(\prod_{i=1}^{n}\sum_{k=1}^K \pi_kN(x_i|\mu_k,\sigma_k))=\sum_{i=1}^nln(\sum_{k=1}^K\pi_kN(x_i|\mu_k,\sigma_k))$
$X=[x_1,x_2,...,x_n]$・・・各データ点
$K$・・・モデルの数(クラスタの数)
がもっとも高くなるようにパラメータを調整してきます。またこれを対数尤度関数と呼びます。
この関数を最大化するようにパラメータを変えたいのですが総和の総和が出現し、解析的に解くことが難しいためEMアルゴリズムを用いて解いていきます。
EMアルゴリズムのやり方としては
Eステップ:期待値の計算
Mステップ:期待値が最大となるようにパラメータの調整
を繰り返すことで最適解を見つけるという方法です。
今回の流れは
- $\pi,\mu,\sigma$の初期値を決める
- 負担率を計算する(Eステップ)
- パラメータ $\pi ,\mu,\sigma$の値を調節する。
- 尤度に差が見られなければ終了。まだ変わるのであれば2に戻る。
という流れで行います。
初期値##
最初の初期値は適当に決めます。(当たり前ですが、この値をなんとなくわかっているなら調整すると早く収束したりするようです。)
Eステップ##
次にEステップです。
ここで負担率という言葉が出てきますが、これはある点xがモデルkより発生した確率です。
先ほどのプロットで考えると、どのガウス分布モデルから生まれた点かわかりませんでした。そのためどのモデルから生まれた点かを示す潜在変数zを考えます。もし$z_{i,k}=1$なら点$x_i$はモデルkから生まれた点であると言えます。
これを式にすると
$p(z_{i,k}=1|x_i)=\frac{p(z_{i,x}=1,x_i)}{p(x_i)}$
また、
$p(x_i|x_{i,k}=1)=\frac{p(z_{i,k}=1,x_i)}{p(z_{i,k}=1)}$
であるため
$p(z_{i,k}=1|x_i)=\frac{p(x_i|z_{i,k}=1)p(z_{i,z}=1)}{p(x_i)}$
である。(ベイズの定理)
また$p(x_i)$はzについて周辺化した値であるため混合ガウス分布の式で表され、
$p(z_{i,k}=1|x_i)=\frac{p(x_i|z_{i,k}=1)p(z_{i,k}=1)}{\sum_{k=1}^{K}\pi_kN(x|\mu_k,\sigma_k)}=\gamma(z_{i,k})$
となります。
ここで、$p(x_i|z_{i,k}=1)$はモデルkより$x_i$が生まれた確率なのでモデルkの正規分布$N(x_i|\mu_k,\sigma_k)$です。
そして、$p(z_{i,k}=1)=\pi_k$であるため
$\gamma(z_{i,k})=\frac{\pi_kN(x|\mu_k,\sigma_k)}{\sum_{k=1}^{K}\pi_kN(x|\mu_k,\sigma_k)}$
となります。
( なぜ$p(z_{i,k}=1)=\pi_k$となるかは、自分の理解が追いついていないのですが、これはあくまでxに関係無い値で、どれだけモデルkに属しやすいかを比べる量とするなら確かにそうなるかもしれないという所感です。)
なぜこれが負担率と言われるかですが、モデルkがどのくらい混合ガウス分布の割合を占めているかを示すからだと考えています。
二つ前の図を見てもらうとなんとなくイメージできるかと思います。
Mステップ##
続いてパラメータの更新です。
個々の方針は$\mu,\sigma$については尤度関数がもっとも高くなればいいので微分してその値が0となる点を探すと言う方針で進めます。
また、$\pi$は$\sum_{k=1}^K\pi_k=1$の条件があるため、ラグランジェの未定乗数法で解いていきます。
この微分の導出はEMアルゴリズム徹底解説ので他の方がとてもわかりやすく説明されているので結果だけをまとめます。個人的に導出して見ましたがとても大変でした
結果
$\mu_k*=\frac{1}{N_k}\sum_{i=1}^N\gamma(z_{i,k})x_i$
$\sigma_k*=\frac{1}{N_k}\sum_{i=1}^N\gamma(z_{i,k})(x_i-\mu_k)(x_i-\mu_k)^T$
$\pi_k*=\frac{N_k}{N}=\frac{\sum_{n=1}^N\gamma(z_{i,k})}{N}$
という結果になります。
混合ガウス分布の実装#
導出についてまとまったので実際に混合ガウス分布のクラスタリングを実装して見ました。
import numpy as np
import matplotlib.pyplot as plt
# difine
data_num = 100
model_num = 3
dim = 2
color = ['#ff0000','#00ff00','#0000ff']
epsilon = 1.0e-3
check = False # if not check == False
# gaussian calculator
def cal_gauss(x,mu,sigma):
return np.exp(-np.dot((x-mu),np.dot(np.linalg.inv(sigma),(x-mu).T))/2)/np.sqrt(2*np.pi*abs(np.linalg.det(sigma)))
# init create param
mu =[]
sigma = []
for i in range(model_num):
mu.append([np.random.rand()*10 ,np.random.rand()*10])
temp = np.random.rand()-np.random.rand()
sigma.append([[np.random.rand()+1,temp],[temp,np.random.rand()+1]])
# create data
values = []
for i in range(model_num):
values.append(np.random.multivariate_normal(mu[i],sigma[i],data_num))
for i in range(model_num):
plt.scatter(values[i][:,0],values[i][:,1],c=color[i],marker='+')
plt.show()
# create training data
train_values =values[0]
for i in range(model_num-1):
train_values = np.concatenate([train_values,values[i+1]])
plt.scatter(train_values[:,0],train_values[:,1],marker='+')
# init model param
model_mu =[]
model_sigma =[]
for i in range(model_num):
model_mu.append([np.random.rand()*10 ,np.random.rand()*10])
temp = np.random.rand()-np.random.rand()
model_sigma.append([[np.random.rand()+1,temp],[temp,np.random.rand()+1]])
model_mu = np.array(model_mu)
model_sigma = np.array(model_sigma)
for i in range(model_num):
plt.scatter(model_mu[i,0],model_mu[i,1],c=color[i],marker='o') #plot pre train mu
temp = []
for i in range(model_num):
temp.append(np.random.rand())
model_pi = np.zeros_like(temp)
for i in range(model_num):
model_pi[i] = temp[i]/np.sum(temp)
plt.show()
# training
old_L = 1
new_L = 0
gamma = np.zeros((data_num*model_num,model_num))
while(epsilon<abs(new_L-old_L)):
#gamma calculation
for i in range(data_num*model_num):
result_gauss = []
for j in range(model_num):
result_gauss.append(cal_gauss(train_values[i,:],model_mu[j],model_sigma[j]))
result_gauss = np.array(result_gauss)
old_L = np.sum(model_pi*result_gauss) #old_L calculation
for j in range(model_num):
gamma[i,j] = (model_pi[j]*result_gauss[j])/np.sum(model_pi*result_gauss,axis=0)
N_k =np.sum(gamma,axis=0)
#calculation sigma
for i in range(model_num):
temp = np.zeros((dim,dim))
for j in range(data_num*model_num):
temp+=gamma[j,i]*np.dot((train_values[j,:]-model_mu[i]).reshape(-1,1),(train_values[j,:]-model_mu[i]).reshape(1,-1))
model_sigma[i] = temp/N_k[i]
#calculation mu
for i in range(model_num):
model_mu[i] = np.sum(gamma[:,i].reshape(-1,1)*train_values,axis=0)/N_k[i]
#calculation pi
for i in range(model_num):
model_pi[i]=N_k[i]/(data_num*model_num)
#check plot
if(check == True ):
gamma_crasta = np.argmax(gamma,axis=1)
for i in range(data_num*model_num):
color_temp = color[gamma_crasta[i]]
plt.scatter(train_values[i,0],train_values[i,1],c=color_temp,marker='+')
for i in range(model_num):
plt.scatter(model_mu[i,0],model_mu[i,1],c=color[i],marker='o')
plt.show()
##new_Lcalculation
for i in range(data_num*model_num):
result_gauss = []
for j in range(model_num):
result_gauss.append(cal_gauss(train_values[i,:],model_mu[j],sigma[j]))
result_gauss = np.array(result_gauss)
new_L = np.sum(model_pi*result_gauss)
gamma_crasta = np.argmax(gamma,axis=1)
for i in range(data_num*model_num):
color_temp = color[gamma_crasta[i]]
plt.scatter(train_values[i,0],train_values[i,1],c=color_temp,marker='+')
for i in range(model_num):
plt.scatter(model_mu[i,0],model_mu[i,1],c=color[i],marker='o')
plt.show()
このような感じで動くはずです。
このプログラムではパラメータが全部ランダムで出しているため、うまくクラスタリングできないこともあります。実際そのようなデータがきたらクラスタリングできないので……
連続隠れマルコフモデルの実装#
かなり遠回りしてしまいましたが、これから連続マルコフモデルの実装を見ていきたいと思います。
連続マルコフモデルである観測情報y={$y_1,y_2,...,y_t$}が得られた時、このモデルがこの値を想起する確率$p(y|M)$はトレリスアルゴリズムでもとめることができます。トレリスアルゴリズムは
$p(y|M) = \sum_{i}\alpha(i,T)$ (ただしこのiは最終状態)
で求められます。
そしてこの$\alpha(i,t)$は
\begin{eqnarray}
\alpha_{i,t}=\left\{ \begin{array}{ll}
\ \pi_i & (t=0) \\
\ \sum_j \alpha(j,t-1)a_{j,i}・b_{i}(y_t) & (t=1,2,...,T) \\
\end{array} \right.
\end{eqnarray}
です。そしてここで出てくる$a_{j,i}$と$b_{j,i}(y_t)$は少し前の話になりますが、隠れマルコフモデルでも出てきた遷移確率と出現確率を示しています。(この話は少し学習とは関係無かったです……)
この$\alpha(i,t)$は前から確率を辿っていきます(フォワード関数)が、これを最後から辿っていく関数(バックワード関数)を定義します。
\begin{eqnarray}
\beta_{i,T}=\left\{ \begin{array}{ll}
\ 1 & (最終状態) \\
\ 0 & (最終状態では無い) \\
\end{array} \right.
\end{eqnarray}
\beta(i,t)=\sum_{j}a_{i,j}・b_{i}(y_t)・\beta(j,t+1) \qquad (t=T,T-1,...,1)
隠れマルコフモデルのモデルパラメータの学習にはEMアルゴリズムの一種であるバウム・ウェルチアルゴリズムを用いて学習することができます。
バウムウェルチアルゴリズムでEステップで計算するのが、
$\gamma(i,j,t)=\frac{\alpha(i,t-1)・a_{i,j}・b_{j}・\beta(j,t)}{p(y|M)}$
この値です。この値は時間tの時状態iからjへ遷移し、かつ$y_t$を出力する時の確率をこのモデルでyが生起する確率で割ったものと考えられます。
そして、パラメータの推定(更新)式は
$\pi*=\frac{\sum_j\gamma(i,j,1)}{\sum_i\sum_j\gamma(i,j,1)}$
$a_{i,j}*=\frac{\sum_t\gamma(i,j,t)}{\sum_t\sum_j\gamma(i,j,t)}$
となり、
bはガウス分布であるため、
$\mu_{i,j}*=\frac{\sum_{t=1}^T\gamma(i,j,t)y_t}{\sum_{t=1}^T\gamma(i,j,t)}$
$\sigma_{i,j}=\frac{\sum_{t=1}^T \gamma(i,j,t)(y_t-\mu_j)(y_t-\mu_j)^t}{\sum_{t=1}^T\gamma(i,j,t)}$
で求められます。
それではコードです。
逐次調整を行なっていたためガウス分布の実装ファイル。隠れマルコフモデルのファイル、実行ファイルの3つに分けています。
(今回当初はGMMーHMMで作る予定だったので実装無駄な部分が多いです。GMMーHMMがうまくいき次第また更新しますので少々お待ちください。)
import numpy as np
import matplotlib.pyplot as plt
import math
import sys
# construct
# c = mixing coefficient
# mu = mean
# sigma = dispersion
# m = model num
# size = datasize
# x = data
## method
# gaussian(x) : calculation gaussian:x=data
# updata(x) : update gmm :x=data
# output(x) : gmm output:x=data (size=1)
class function_b:
upsilon = 1.0e-50
def __init__(self,c,mu,sigma,m,size,x):
self.c = np.array(c)
self.c = self.c.reshape((-1,1))
self.mu = np.array(mu)
self.mu = self.mu.reshape((-1,1))
self.sigma = np.array(sigma)
self.sigma = self.sigma.reshape((-1,1))
self.size = size
self.model_num = m
self.x = np.array(x).reshape(1,-1)
self.ganma = np.zeros((self.model_num,self.size))
self.sum_gaus = 0
self.N_k=np.zeros(self.model_num)
def gaussian(self,x):
return np.exp(-((x-self.mu)**2)/(2*self.sigma))/np.sqrt(2*math.pi*self.sigma)
def update(self,pre_ganma):
#x=[x1~xt]
self.ganma = np.zeros((self.model_num,self.size))
#calculate ganma
for m in range(self.model_num):
self.ganma[m] = pre_ganma*((self.c[m]*self.gaussian(self.x)[m]+function_b.upsilon)/np.sum(self.c*self.gaussian(self.x)+function_b.upsilon,axis=0))+function_b.upsilon
for m in range(self.model_num):
self.N_k[m] = np.sum(self.ganma[m])
#calculate c
for m in range(self.model_num):
self.c[m]=self.N_k[m]/np.sum(self.N_k)
#calculate sigma
for m in range(self.model_num):
self.sigma[m]=np.sum(self.ganma[m]*((self.x-self.mu[m])**2))/self.N_k[m]
#calculate mu
for m in range(self.model_num):
self.mu[m]=np.sum(self.ganma[m]*self.x)/self.N_k[m]
def output(self,x):
return np.sum(self.c.reshape((1,-1))*self.gaussian(x).reshape((1,-1)))
import numpy as np
import sys
import matplotlib.pyplot as plt
from class_b import function_b
import copy
# construct
# s = state num
# x = data
# pi = init prob
# a = transition prob
# c = gmm mixing coefficient
# mu = gmm mean
# sigma = gmm dispersion
# m = gmm model num
# method
# cal_alpha() : calculation alpha
# cal_beta() : calculation beta
# cal_exp() : calculation expected value(?)
# update() : update prams
# makestatelist : make statelist
# viterbi : viterbi algorithm
class Hmm_Gmm():
upsilon=1.0e-300
def __init__(self,s,x,pi,a,c,mu,sigma,m):
self.s = s
self.x = x
self.a = np.array(a)
self.size=len(x)
self.b=[]
for i in range(s):
self.b.append(function_b(c[i],mu[i],sigma[i],m,self.size,x))
self.pi = np.array(pi)
self.alpha = np.zeros((self.s,self.size))
self.beta = np.zeros((self.s,self.size))
self.prob = None
self.kusai = np.zeros((self.s,self.s,self.size-1))
self.ganma = np.zeros((self.s,self.size))
self.preganma = None
self.delta = None
self.phi = None
self.F = None
self.P = None
self.max_statelist=None
def cal_alpha(self):
for t in range(self.size):
for j in range(self.s):
if t==0:
self.alpha[j,t]=self.pi[j]*self.b[j].output(self.x[t])
else:
self.alpha[j,t]=0
for i in range(self.s):
self.alpha[j,t]+=self.alpha[i,t-1]*self.a[i,j]*self.b[j].output(self.x[t])
self.prob =0
for i in range(self.s):
self.prob+=self.alpha[i,self.size-1]+Hmm_Gmm.upsilon
def cal_beta(self):
for t in reversed(range(self.size)):
for i in range(self.s):
if t ==self.size-1:
self.beta[i,t]=1
else:
self.beta[i,t]=0
for j in range(self.s):
self.beta[i,t]+=self.beta[j,t+1]*self.a[i,j]*self.b[j].output(self.x[t+1])
def cal_exp(self):
for t in range(self.size-1):
for i in range(self.s):
for j in range(self.s):
self.kusai[i,j,t] = ((self.alpha[i,t]*self.a[i,j]*self.b[j].output(self.x[t+1])*self.beta[j,t+1])+(Hmm_Gmm.upsilon/(self.s)))/self.prob
for t in range(self.size):
for i in range(self.s):
#self.ganma[i,t] = (self.alpha[i,t]*self.beta[i,t])/self.prob
#self.ganma[i,t] = (self.alpha[i,t]*self.beta[i,t])/self.prob + Hmm_Gmm.uplilon
self.ganma[i,t] = ((self.alpha[i,t]*self.beta[i,t])+(Hmm_Gmm.upsilon))/self.prob
def update(self):
#cal exp
self.cal_alpha()
self.cal_beta()
self.cal_exp()
#cal pi
self.pi = self.ganma[:,0]
#cal a
for i in range(self.s):
for j in range(self.s):
#self.a[i,j]=np.sum(self.ganma[i,:])
self.a[i,j]=np.sum(self.kusai[i,j,:])/np.sum(self.ganma[i,:])
#self.a[i,j]=np.sum(self.kusai[i,j,:])
#cal b
#cal preganma
self.preganma = np.zeros((self.s,self.size))
for t in range(self.size):
temp = self.alpha[:,t]*self.beta[:,t]+self.upsilon
self.preganma[:,t] = temp/np.sum(temp)
for i in range(self.s):
self.b[i].update(np.array(self.preganma[i]))
def makestatelist(self,f,size):
statelist = np.zeros(size)
for t in reversed(range(size)):
if t == size-1:
statelist[t] = f
else:
statelist[t] = self.phi[statelist[t+1],t+1]
return statelist
def viterbi(self,x):
data=np.array(x)
self.delta = np.zeros((self.s,data.shape[0]))
self.phi = np.zeros((self.s,data.shape[0]))
for t in range(data.shape[0]):
for i in range(self.s):
if t == 0:
self.phi[i,t] = np.nan
self.delta[i,t] = np.log(self.pi[i])
else:
self.phi[i,t] = np.argmax(self.delta[:,t-1]+np.log(self.a[:,i]))
self.delta[i,t] = np.max(self.delta[:,t-1]+np.log(self.a[:,i]*self.b[i].output(data[t])+self.upsilon))
self.F = np.argmax(self.delta[:,data.shape[0]-1])
self.P = np.max(self.delta[:,data.shape[0]-1])
#print(self.makestatelist(self.F,data.shape[0]))
self.max_statelist=self.makestatelist(self.F,data.shape[0])
import numpy as np
import matplotlib.pyplot as plt
import sys
from class_hmm_gmm import Hmm_Gmm
model_num = 1
state_num = 4
color=['#ff0000','#00ff00','#0000ff','#888888']
value_size = int(10*model_num*state_num)
create_mu = []
create_sigma= []
create_pi =[]
for i in range(state_num):
temp = []
temp1 = []
temp2=[]
for j in range(model_num):
temp.extend([(np.random.rand()*30-np.random.rand()*30)])
temp1.extend([np.random.rand()+1])
temp2.extend([np.random.rand()])
create_mu.append(temp)
create_sigma.append(temp1)
create_pi.append((temp2/np.sum(temp2)).tolist())
# create data
values = []
for i in range(state_num):
temp = []
for it in range(int(value_size/state_num/model_num)):
for j in range(model_num):
temp.extend(np.random.normal(create_mu[i][j],create_sigma[i][j],1).tolist())
values.append(temp)
x_plot = np.linspace(0,value_size,value_size)
for i in range(state_num):
plt.scatter(x_plot[i*len(values[0]):i*len(values[0])+len(values[0])],values[i],c=color[i],marker='+')
for i in range(state_num):
for j in range(model_num):
plt.plot(x_plot[i*len(values[0]):i*len(values[0])+len(values[0])],np.full(len(values[0]),create_mu[i][j]),c=color[i])
plt.show()
train_values=[]
for i in range(state_num):
train_values.extend(values[i])
train_mu = []
train_sigma= []
train_pi =[]
for i in range(state_num):
temp = []
temp1 = []
temp2=[]
for j in range(model_num):
temp.extend([np.random.rand()*30-np.random.rand()*30])
temp1.extend([np.random.rand()+1])
temp2.extend([np.random.rand()])
train_mu.append(temp)
train_sigma.append(temp1)
train_pi.append((temp2/np.sum(temp2)).tolist())
## backup train
b_train_mu = train_mu
b_train_sigma = train_sigma
plt.scatter(x_plot,train_values,c="#000000",marker='+')
for i in range(state_num):
for j in range(model_num):
plt.plot(x_plot[i*len(values[0]):i*len(values[0])+len(values[0])],np.full(len(values[0]),train_mu[i][j]),c=color[i])
plt.show()
# init a
a = []
for j in range(state_num):
temp = []
for i in range(state_num):
temp.append(np.random.rand())
a.append(temp)
for i in range(state_num):
for j in range(state_num):
#a[j][i] = a[j][i]/np.sum(np.array(a)[:,i])
a = (np.array(a)/np.sum(np.array(a),axis=0)).tolist()
# init init_prob
init_prob = []
for j in range(state_num):
temp2.extend([np.random.rand()])
# temp2[0]+=1
init_prob.extend((temp2/np.sum(temp2)).tolist())
# init Hmm_Gmm model
hmm_gmm = Hmm_Gmm(state_num,train_values,init_prob,a,train_pi,train_mu,train_sigma,model_num)
# train roop
print(create_mu)
print(a)
count = 0
while(count != 100):
hmm_gmm.update()
count +=1
# viterbi
hmm_gmm.viterbi(train_values)
print(hmm_gmm.max_statelist)
# *************************************
plt.scatter(x_plot,train_values,c="#000000",marker='+')
## plot of init train mu
for i in range(state_num):
for j in range(model_num):
plt.plot(x_plot[i*len(values[0]):i*len(values[0])+len(values[0])],np.full(len(values[0]),b_train_mu[i][j]),c="#dddddd")
for i in range(state_num):
for j in range(model_num):
plt.plot(x_plot[i*len(values[0]):i*len(values[0])+len(values[0])],np.full(len(values[0]),hmm_gmm.b[i].mu[j]),c=color[i])
plt.show()
結果
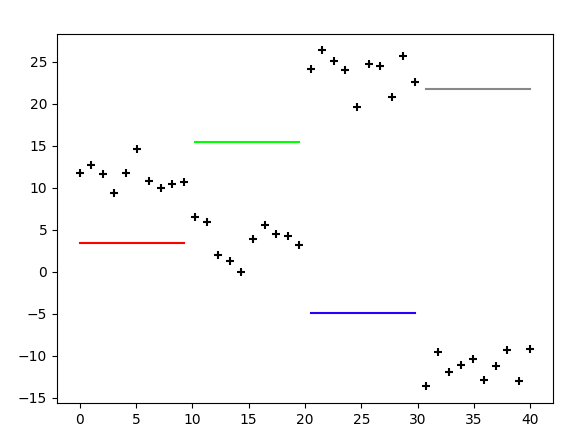
初期$\mu$の値とガウス分布から出力された点です。今回は4つの状態を仮定していて4つのガウス分布からそれぞれ点が生成されています。それぞれの状態を最初から順に状態1(赤)、状態2(緑)、状態3(青)、状態4(灰)と呼んでおきます。
平均値 $\mu$を乱数でリセットしました。
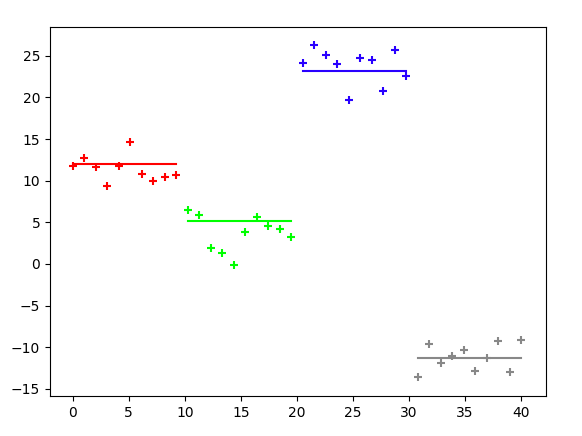
これに対して学習を行なっていきます。100回アップデートした結果です。
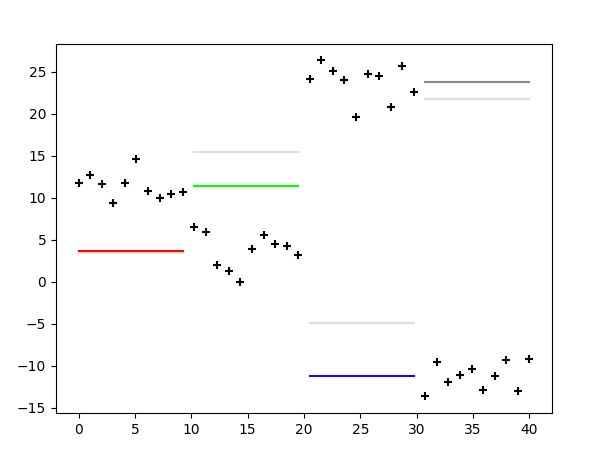
学習結果です。
状態は最初から順に状態2、状態1、状態4、状態3の順番で状態づきましたが、結果としてうまくいっているように感じます。
最後に##
今回は隠れマルコフモデルについて自分なりにまとめてみましたが、思った以上に量が多く、数ヶ月前に実装したのにどうやって考えるのか忘れてしまうところも多く早めにアウトプットしていくことは大事だなととても感じました。その影響もあってビタービアルゴリズムや、状態リストの関数など説明できてないので。また後日改めてまとめます。(文章力なくて入れ込めなかった原因もありますが……)
また、このプログラムでもきちんとガウス分布がうまくはまらないこともあり、自分のプログラムが原因なのか、局所最適解に落ちているのかもう少し考えたいと思います。
また、GMM-HMMの実装も行なってみたのですが(model_numを変更するとGMMになる)、うまく状態つかなくて、ここも再度どこでうまくいっていないのか(もしくは局所最適解に落ちているのか)もう一度見直したいと考えています。
きちんと完成したものじゃなくて申し訳ないです。
また、局所最適解に落ちる問題を解決するための手法について書かれてそうな論文見つけたのでこちらも勉強していきます。
[参考]##
https://mieruca-ai.com/ai/markov_model_hmm/ 【技術解説】マルコフモデルと隠れマルコフモデル
https://qiita.com/kenmatsu4/items/59ea3e5dfa3d4c161efb EMアルゴリズム徹底解説