HousePricesで機械学習の外れ値処理を考える(1)

目次

はじめに
HousePrices概要

外れ値とは
　外れ値の定義
　外れ値と異常値の差異

HousePricesで１次元の外れ値検定を行なってみる
　スミルノフ=グラブス検定による除去
　四分位範囲（IQR）を用いた除去
　トリム平均（上下5.0%）
　比較

おわりに
参考資料

はじめに（本稿の目標）

　私は現在会社で機械学習案件・データ分析の獲得を目指すチームでキャッチアップを進めています。
その中で、社内LT用に住宅価格予測のknowledgeコンペをもとに色々調べていると、外れ値の処理について色々疑問だったので今回調べてみようと思います。

本稿の目標は、機械学習の外れ値の処理について一般的な手法を網羅的に学習し、住宅価格予測のデータセットを用いて各手法の特徴を可視化することになります。

HousePrices概要

住宅購入者に夢の家の説明を尋ねても、地下室の天井の高さや東西鉄道への近さなどから始めることはおそらくないでしょう。 しかし、この遊び場の競争のデータセットは、寝室の数や白いピケットフェンスよりもはるかに価格交渉に影響を与えることを証明しています。

このコンペではアイオワ州エイムズの住宅の79 の説明変数を使用して、各住宅の最終価格（SalePrice)を予測することが求められます。kaggle入門で有名なspaceship titanicと同じ練習用のコンペになります。

外れ値とは

外れ値の定義

　そもそも外れ値の定義とはなんでしょうか？ wikipediaによると、x1 を標本値、μ は平均、σ は標準偏差とし次式によって算出される検定統計量τ1を求め、これが有意水準（αまたはアルファとも呼ばれる）を下回った値を外れ値として検定を行う、といった感じです。（zスコア検定）

zスコアは、それぞれのデータの点数を平均点を0、標準偏差を1になるように変換した値のこと。これによりデータは相対的な位置を知ることができる。

τ_{1} = \frac{x_1 - μ}{σ}

より精密には、正規分布を仮定して、スミルノフ・グラブス (Smirnov‐Grubbs) 検定を使います。

サンプルサイズを n、所要の有意水準を α、自由度 n - 2 のt分布の α / n × 100 パーセンタイルを t として

t = \frac{（n-1)t}{\sqrt{n(n-2)+nt^2}}

※有意水準は一般的に0.05（5%）とすることが適切とされています。（この数字の意味については今回割愛します）前者の手法だと有意水準の境界となる有意点を求める必要があります。

外れ値と異常値の差異

・外れ値と異常値
外れ値とは文字通り「他のデータと比べて極端に離れた値」のことを指します。他と比べて極端に小さな値、あるいは極端に大きな値を言います。それら「外れ値」の中でも、外れている理由が判明しているものが「異常値」です。たとえば保育園の園児たちの身長を測ったデータセットに、160cmというデータが含まれていたときのことを考えてみましょう。他のデータは50cm～113cmの範囲で、160cmは明らかに離れています。そこでデータを確認したら、160cmは園児たちの測定値ではなく、保育士さんの測定値が誤って入ってしまっていた。これが異常値で、もし分析の目的が園児たちの身長の把握であるならば、保育士さんのデータは分析対象外とする、という対処を取ることになります。しかし、もしこのデータの取得背景がわからなければ（今回のケースではありえないですが）慎重に扱う必要があります。また、身長のデータの中に、数字ではなく文字列や記号などが入っているケースもあるでしょう。これらは異常値とは呼ばず、ノイズと呼びます。外れ値と異常値はこのように異なるものですが、英語では同じ「outlier」と言います。

　このコラムが非常に腑に落ちる解説になっていました。私のような素人が普段無意識に除いているのは理由のある異常値で、データから理由をつけて除くべきものが外れ値、というわけでした。kaggleコンペではこの辺を意識する必要はなさそうですが、現実のデータを扱うならば気をつけるべき事柄だと思います

HousePricesで１次元の外れ値検定を行なってみる

　１次元のデータで外れ値を除くというのは、例えば他のデータとの相関を考えたとき不自然でないデータが覗かれるなど、やや実データの性質から離れるような感覚がありますが、手法の検証という観点から、今回はHousePricesの量的データのうち、SalePrice(販売価格)について外れ値検定を実施します。
今回の目的は住宅価格予測のデータセットを用いて各手法の特徴を可視化することになりますので、合わせて以下の手法で外れ値除去を行い、これらを比較していこうと思います。

• スミルノフ=グラブス検定による除去
• 四分位範囲（IQR）を用いた除去
• トリム平均（上下10%）

スミルノフ=グラブス検定による除去

　今回はこちらの外れ値検定（スミルノフ=グラブス検定）pythonの実装
から実装をお借りして、外れ値除去を行います。

# スミルノフ=グラブス検定による除去
print(train_df.shape[0])

def func_tau(x, alpha):
    n = x.size
    t = stats.t.isf((alpha/n)/2, n-2) #両側
    tau = (n-1)/np.sqrt(n) * np.sqrt(t**2/(n-2 + t**2))
    return tau

def Smirnov_Grubbs(x, alpha):
    x_ini = x
    while(True):
        mean = np.mean(x)
        std = np.std(x, ddof=1)
        imax, imin = np.argmax(x), np.argmin(x)
        itest = imax if np.abs(x[imax] - mean) > np.abs(x[imin] - mean) else imin

        test =  np.abs(x[itest] -mean)/std
        tau = func_tau(x, alpha)

        if(test > tau):
            x = np.delete(x, itest)
        else:
            break

    x_outlier = np.setdiff1d(x_ini,x) 
    return x_outlier


smirnov_grobbs = Smirnov_Grubbs(train_df['SalePrice'].values, 0.05)
outliers = train_df[train_df['SalePrice'].isin(outliers)][['YearBuilt', 'LotArea', 'SalePrice']]

print(outliers.shape[0]) # 外れ値個数：

# 結果の表示
print("最大値:\n", outliers[['YearBuilt', 'LotArea', 'SalePrice']].max())
print("\n最小値:\n", outliers[['YearBuilt', 'LotArea', 'SalePrice']].min())
print("\n中央値:\n", outliers[['YearBuilt', 'LotArea', 'SalePrice']].median())

#result
# 外れ値個数 11
# 最大値:
#  YearBuilt      2009
# LotArea       53504
# SalePrice    755000
# dtype: int64

# 最小値:
#  YearBuilt      1892
# LotArea       12919
# SalePrice    475000
# dtype: int64

# 中央値:
#  YearBuilt      2005.0
# LotArea       16056.0
# SalePrice    556581.0
# dtype: float64

四分位範囲（IQR）を用いた除去

# 四分位範囲（IQR）を用いた除去
print(train_df.shape[0])

def Iqr_Outlier_Removal(data, column):
    Q1 = data[column].quantile(0.25)
    Q3 = data[column].quantile(0.75)
    IQR = Q3 - Q1
    lower_bound = Q1 - 1.5 * IQR
    upper_bound = Q3 + 1.5 * IQR

    # return data[(data[column] >= lower_bound) & (data[column] <= upper_bound)]
    return data[(data[column] >= lower_bound) & (data[column] <= upper_bound)]

filtered_df = Iqr_Outlier_Removal(train_df, 'SalePrice')
outliers = train_df[~train_df.index.isin(filtered_df.index)][['YearBuilt', 'LotArea', 'SalePrice']]

print(outliers.shape[0]) # 外れ値個数：61

# 結果の表示
print("最大値:\n", outliers[['YearBuilt', 'LotArea', 'SalePrice']].max())
print("\n最小値:\n", outliers[['YearBuilt', 'LotArea', 'SalePrice']].min())
print("\n中央値:\n", outliers[['YearBuilt', 'LotArea', 'SalePrice']].median())


#result
# 1460
# 外れ値個数 61
# 最大値:
#  YearBuilt      2010
# LotArea      215245
# SalePrice    755000
# dtype: int64

# 最小値:
#  YearBuilt      1892
# LotArea        5587
# SalePrice    341000
# dtype: int64

# 中央値:
#  YearBuilt      2006.0
# LotArea       13682.0
# SalePrice    394617.0
# dtype: float64

トリム平均（上下5.0%）

# トリム平均（上下5.0%）
print(train_df.shape[0])

def Ration_Removal(data, column, ratio):
    lower_bound = data[column].quantile(ratio)
    upper_bound = data[column].quantile(1 - ratio)

    # return data[(data[column] >= lower_bound) & (data[column] <= upper_bound)]
    return data[(data[column] >= lower_bound) & (data[column] <= upper_bound)]

filtered_df = Ration_Removal(train_df, 'SalePrice', 0.05)
outliers = train_df[~train_df.index.isin(filtered_df.index)][['YearBuilt', 'LotArea', 'SalePrice']]


# 結果の表示
print("外れ値個数", outliers.shape[0]) 
print("最大値:\n", outliers[['YearBuilt', 'LotArea', 'SalePrice']].max())
print("\n最小値:\n", outliers[['YearBuilt', 'LotArea', 'SalePrice']].min())
print("\n中央値:\n", outliers[['YearBuilt', 'LotArea', 'SalePrice']].median())

# 1460
# 外れ値個数 144
# 最大値:
# YearBuilt      2010
# LotArea      215245
# SalePrice    755000
# dtype: int64

# 最小値:
# YearBuilt     1892
# LotArea       1477
# SalePrice    34900
# dtype: int64

#中央値:
# YearBuilt      1972.5
# LotArea       10182.5
# SalePrice    328450.0
# dtype: float64

比較

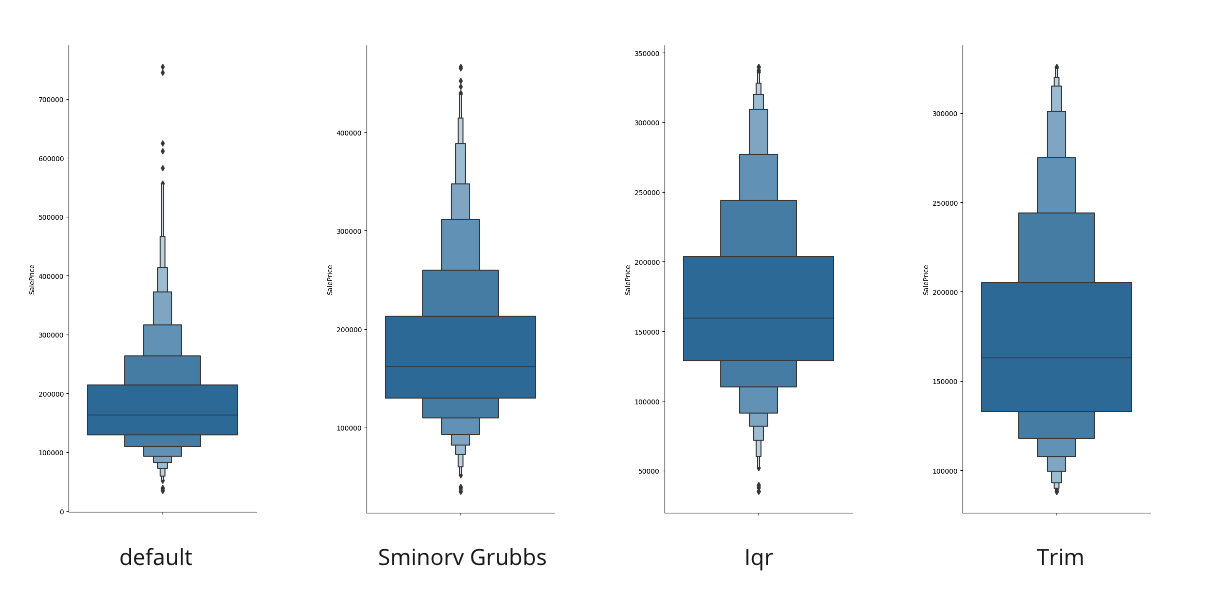
SalePriceにおける各手法の外れ値データセットの特徴は次の図のようになりました。

	SmirnovGrubbs	四分位範囲	トリム平均
Max	755000	755000	755000
Min	475000	341000	34900
Median	556581.0	394617.0	328450.0
個数	11	61	144

箱ひげ図比較

　以上から考察できることとしては以下のようなことでしょうか？？（これだけでも多分他にもっと考えられる。。）
・Smirnov Grubbs検定で外れ値を回帰的に除去した時、他２手法に比べ破壊率が少ないため元のデータフレームの傾向を最も強く反映していると言える
・Trimした場合、データフレームのボリュームゾーンと呼べる範囲が、データ範囲に占める割合が高くなり、強調されている
・四分位範囲で除去をした時、元データフレームの最小値外れ値として除かず、妥当な値として処理している。

考察

　少なくともいくつかのkaggleのnoteでは、スコアの高いモデルを構築するために外れ値を除くことを説明なしに行なっています。また体感ではありますがそれが高いスコアに結びつく要因の一つになっているとも考えています。評価基準は提出用のデータに比べ、モデルから算出されたデータがどの程度近いかですから、全体の1%に満たない外れ値を考慮外とすることは自然に思えます。

　しかし、現実のデータセットの解析を行うときは、外れ値を慎重に扱う必要があることと思います。外れ値として除く値が異常値なのか、どういった要因で外れ値となっているのか、構築するモデルの役割対象範囲はどこからどこまでなのかなど、本来の目的を達成するという観点から、それを除くことの妥当性を明文化することは重要と思いました。
　 例えば、歴史的価値のある物凄くお高い家がデータセットに混じっていたとして、これをモデルの対象外と明示することができれば、適用範囲に条件はつきますがより実用的な学習モデルに近づくのではないでしょうか。ただこれは外れ値というよりは異常値と言ったほうが適切ですし、多次元的に解析はやはり必須に思えました。

　今回のHousePriceのデータならば、厳密に絞り込んだ１０個程度のデータからそれらを吟味したのち、手動で取り除くのが丁寧なやり方と言えるのではないでしょうか？

（2）では、二次元的な検証とスコアとの相関も調べる予定です。

　ただまぁ身も蓋もないことをいうと、kaggleでハイスコアを取ることを考えたら、こんなこと検証するよりモデルの選定とかチューニングとか他の特徴量エンジニアリング頑張った方がスコアは伸びると思います。

参考資料

House Prices - Advanced Regression Techniques
【Kaggle】「House Prices」をパクりながらやってみた。
wikipedia 外れ値
Minitab20サポート 外れ値検定の主要な結果を解釈する
【初心者】特徴量エンジニアリング（外れ値）について調べてみた
社会人生活の実験室 外れ値検定（スミルノフ=グラブス検定）pythonの実装