概要
下記の論文にて新しい異常検知手法DAGMMが提案されました.それをChaienrというフレームワークで実装してみたという記事です.そこで疑問なこと,困ったことを本記事に記載しました.お気付きの点がありましたらフィードバックでも頂けると幸いです.
-
Deep Autoencoding Gaussian Mixture Model for Unsupervised Anomaly Detection [Bo Zong et al (2018)]
また,参考にさせていただいた記事は以下です.DAGMMについてわかりやすく説明されています. - https://qiita.com/ToshihiroNakae/items/5863fd70ed9afc5fd6cd
- https://www.slideshare.net/ChihiroKusunoki/ss-98822807
- http://cookie-box.hatenablog.com/entry/2018/05/18/004544
これまでの異常検知するためのアプローチ方法
正常データのみを学習させる方法としては最近ではAutoEncoderの再構築誤差を用いた異常検知や,GANを用いた方法などもありますね.ニューラルネット系がトレンドなのはアーキテクチャーを柔軟に組みやすいかつ,パラメータ最適化の方法が考えやすいからなのでしょうか.しかし,現在でも次元削減と密度推定の2段階踏むのが異常検知の常套手段のようです,多く採用されているそうです(私がそう感じているだけかもしれませんが...).例えば,主成分分析(PCA)で次元削減した後に混合ガウスモデルをEMアルゴリズムでパラメータ推定して異常検知などでしょうか.この次元削減の部分をAutoEncoderの潜在変数を用いる方法とかもありますね.または,密度推定の部分を1ClassSVMを採用するやり方とかも見たことがあります.
今回取り上げた論文ではこのような2段階のステップを踏むところに対し以下の問題点を挙げています.
- 次元削減は次元削減で、密度推定は密度推定で学習しているために局所最適解に陥りやすい(たしかに)
- 次元削減の段階で異常検知に必要な情報が失われてしまう可能性がある(その可能性は否めない)
- 次元削減と密度推定を同時に行う手法があるが,次元削減が線形かつ密度推定のモデルが単純すぎるため表現力が乏しい(非線形な次元削減はAutoEncoderでいけそう)
- 次元削減した後,元の次元へ復元したときの再構築誤差が考慮されていない(おっ これもAutoEncoderの分野)
DAGMM
そこでこれらを解決するための手法がDAGMMであり、以下の3種のモデルで構成されています.
- Compression Network : AutoEncoderの潜在変数と再構築誤差をconcatしたものを出力する.
- Estimation Network : 上記の出力を元に,混合ガウスモデル内の各クラスに対し,どれくらいの確率で分類されるかを出力するモデル
- エネルギー計算 : 1の出力と2の出力より,GMMに対する負の対数尤度を計算する(論文中ではこれをエネルギーと読んでいる)
以下が論文で示している概要図である.(3)は省略されている.
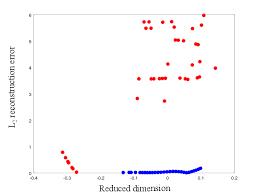
1のCompression Network では潜在変数と再構築誤差を合体させているが,これはどちらも異常検知する上で重要な情報であるだろうと考えているようだ.これは論文中に掲載されている以下の図を見ると明らかだ.横軸が1次元に次元削減した時の値,縦軸が再構築誤差の値を示している.青が正常で赤が異常.
1,2のモデルは図からもわかる通りニューラルネットで構築可能である.3のモデルに関しても混合比,平均ベクトル,分散共分散行列を計算した上で負の対数尤度を計算するが,これは計算グラフで構築することが可能である.よって誤差逆伝播でパラメータを学習することが可能である.なのでフレームワークを用いれば比較的容易に実装できる.
学習する際の目的関数は
再構築誤差(L2ノルムの2乗)+ 3で計算されたエネルギー + 正則化項
でありこれが最小になるようパラメータを最適化していく.
実際にあるデータに対して異常か否かを判定するときは,3のエネルギーが閾値異常であれば異常と判定するようだ.
上記についての詳細は論文や参考記事を参照してください.
Chainerで実装してみた
githubで公開しています.
結構長いのでここには埋め込みません.
扱ったデータセットは論文中でも取り上げられた Arrhythmiaデータセットを用いました.
今回は正常データを正常として学習(上記論文中では正常以外ラベルのうちのいくつかのラベルも正常とみなして学習した).
ハイパーパラメータは全て同じにしました.
学習
以下の図は学習の様子つまり誤差の推移を示しています.横軸がepoch数,縦軸が誤差です.
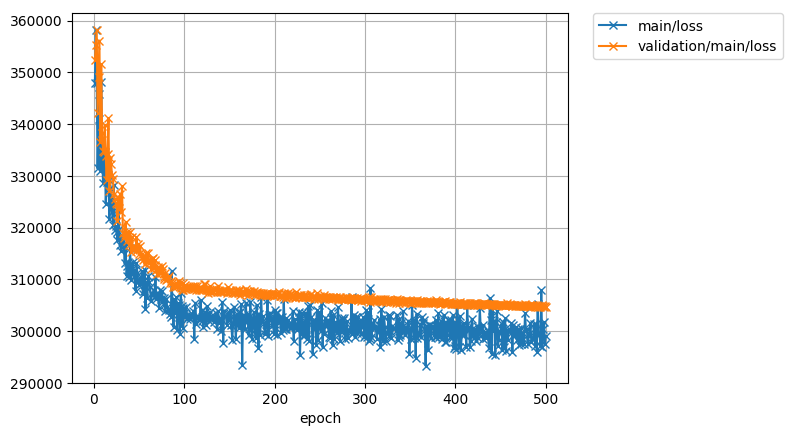
とりあえず500回まで学習させた様子を載せました.まだ学習させればもうちょい下がりそうです.といっても多分ほんのちょっと
しかし気になるのは誤差の値です.30万前後ですと...
目的関数内の再構築誤差は論文中ではL2ノルムの2乗となっていました.なのでそれに準じて実装しましたが...ふつう回帰問題ではMSEなどが損失関数として用いられますが...
論文の読み間違えなのかコードのミスなのか...
テスト
論文中ではテスト時にenergyが大きいほど異常と推定するようであるが,2の出力であるgammaや,Autoencoder(Compression Network)で再構築した時の誤差をヒストグラムで色別(正常(学習,検証),異常)で可視化できるようにしてみた.さらにAutoencoder(Compression Network)の潜在変数zも可視化できるようにしてみた.詳細はgithubのreadmeを参照してください.
疑問点
- 目的関数内の再構築誤差はなぜMSEではなくL2ノルムの2乗なのか
- 先ほどのグラフを見ると収束しがちであるが,論文中では同データセットで100000回学習させている.どういうことなのか
- いざ異常検知する際,正常データに関するgammaとzから計算される混合比,平均ベクトル,分散共分散行列を利用するが,これは最後のミニバッチによって計算されたものを使うのか,正常データ全体を用いて順伝播させ計算し,それを使うのかが謎.
- Chianerのモデル保存で混合比,平均ベクトル,分散共分散行列のような単なる変数も保存したいがそれは可能なのか? 色々試した限りできなかったから現状はcsvファイルとしていちいち書き出している.
- 他のフレームワークによる実装がgithub上でいくつかあるが,これらよりもコードが長くなってしまったのはChainerだから仕方ないことなのか? 調べた限り,numpyのような配列同士のブロードキャスト演算ができないので,配列のshapeを揃える作業がかなり入ってしまう.いい策がないものなのか...
今後の課題
まず,もうちょい学習させてみようと思います.
また別のデータセットに対して畳み込みニューラルネットを用いたAutoEncoderで試したが共分散行列の行列式が0になったり逆行列が求まらなかったりする.同様にCompression Networkの潜在変数の次元を小さくしないと,共分散行列の行列式が0になったり逆行列が求まらなかったりする.これらの対策として,共分散行列の対角成分に微量を加算するという作業もしたりしたが,epochが進むとやはり同様の問題が起こり,負の対数尤度が発散してしまいました.
そこでコレスキー分解を用いた算出方法でも実装する必要があるかなと考えました。
最後に
ざっと急いで書いたから雑な文章になってしまいました。すみません。
今後気づいた点や,書き忘れたことなど思い出したら,追記していきたいとおもいます。