もともとの動機は、LSTMなどのRNN周辺分野のアルゴリズムをしっかりと理解したいことでした。
その一方で、ニューラルネット関連については、仕組みはなんとなく理解していたのですが、隠れ層の振る舞いや学習のアルゴリズム等をしっかり理解しきれているかどうかの自信がなかったので、0から作ってみることにしました。
ちなみに、0から作るというのは、既存の機械学習ライブラリを使わない、という程度の意味です。
勉強目的でもなければ、既存のOSSの機械学習ライブラリを使ったほうが圧倒的に楽ですし、学習も早いでしょうし、バグに悩まされる可能性は低いと思いますし、そこだけ注意してください。。
将来的にはRNN、LSTMの順に構築していきたいのですが、この記事ではフィードフォーワードモデルを構築し、隠れ層の挙動を確認するところまでにしておきたいと思います。
また、既にPythonを用いたサンプルコードがたくさんありますが、敢えてパラダイムの違う関数型言語で構築することで、ちゃんと理解できているかどうか明白にしようと思います。
...なんて言っていますが、なによりClojureが好きだという理由が大きかっただけです。
それと、計算効率や並行処理などはもちろん現段階では考慮していません。
加えて、Clojureでの開発環境や基本についても、もちろん扱いませんのであしからず。
一応project.cljを晒しておきます。
最後のほうで、ニューラルネットの出力を確認するためにincanterを使うよ!
(defproject nn "0.1.0-SNAPSHOT"
:description "FIXME: write description"
:url "http://example.com/FIXME"
:license {:name "Eclipse Public License"
:url "http://www.eclipse.org/legal/epl-v10.html"}
:dependencies [[org.clojure/clojure "1.7.0"]
[incanter "1.5.6"]])
では、早速みて行きましょう。
ユニット
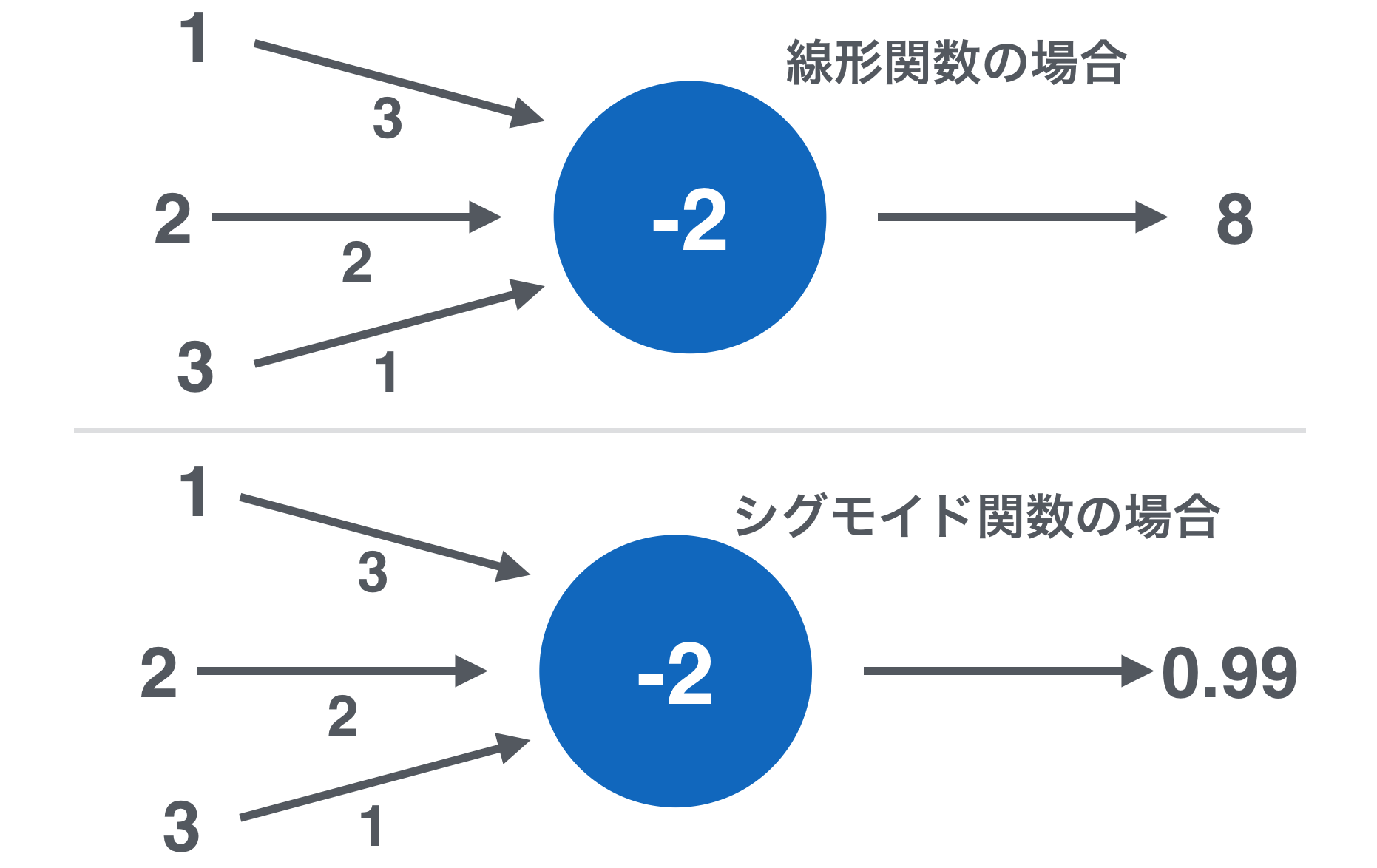
上図のように、ユニットは、入力元となる別ユニットの出力に重み付けしたものを受け取って、それらとバイアスを足しあわせて、活性化関数を通して何かしらの値を出力します。
矢印の根の値がこのユニットに入ってくる別ユニットの出力、矢印の側の値が重みの値、青円の中の値がバイアスです。
バイアスに関しては閾値という表現をすることもありますね。
改めて思ったのですが、ユニットの活性化関数が線形関数の場合は、式だけなら重回帰と同じですね。
活性化関数
活性化関数は、シグモイド関数の場合、次のようにコードで記述出来ます。
(defn sigmoid [x]
(/ 1 (+ 1 (exp (- x)))))
活性化関数が線形関数の場合には、(fn [x] x)といった、入力を変換せずに返り値とする関数となりますね。
他にも隠れ層で活用される関数は、tanhや、Rectifier(ReLU)などがあり、とりわけ出力層などでは回帰をする場合は線形関数、確率分布を出力としたい場合、softmaxを扱うようですね。
今回はスタンダードなシグモイド関数と線形関数の2つのみで話を進めていきます。
ユニットの入力と出力
(defn unit-output [input-list w-list bias activate-fn-key]
(let [activate-fn (condp = activate-fn-key
:sigmoid sigmoid
:linear identity)]
(->> (mapv * input-list w-list)
(cons bias)
(reduce +)
activate-fn)))
->>マクロ以降がこの関数の本質です。
このユニットへの入力と重みを掛けあわせ配列を作成します。
次に、バイアスも配列に追加し、すべて足しあわせます。
最後に、活性化関数に通したものが、この関数の出力になります。
試しに計算をして、出力を確認してみましょう。
(unit-output [1 2 3] [3 2 1] -2 :linear) => 8
(unit-output [1 2 3] [3 2 1] -2 :sigmoid) => 0.9996646498695336
(unit-output [2 4 -3] [-4 2 1] 1 :linear) => -2
(unit-output [2 4 -3] [-4 2 1] 1 :sigmoid) => 0.11920292202211755
大丈夫そうですね!
ニューラルネットワーク
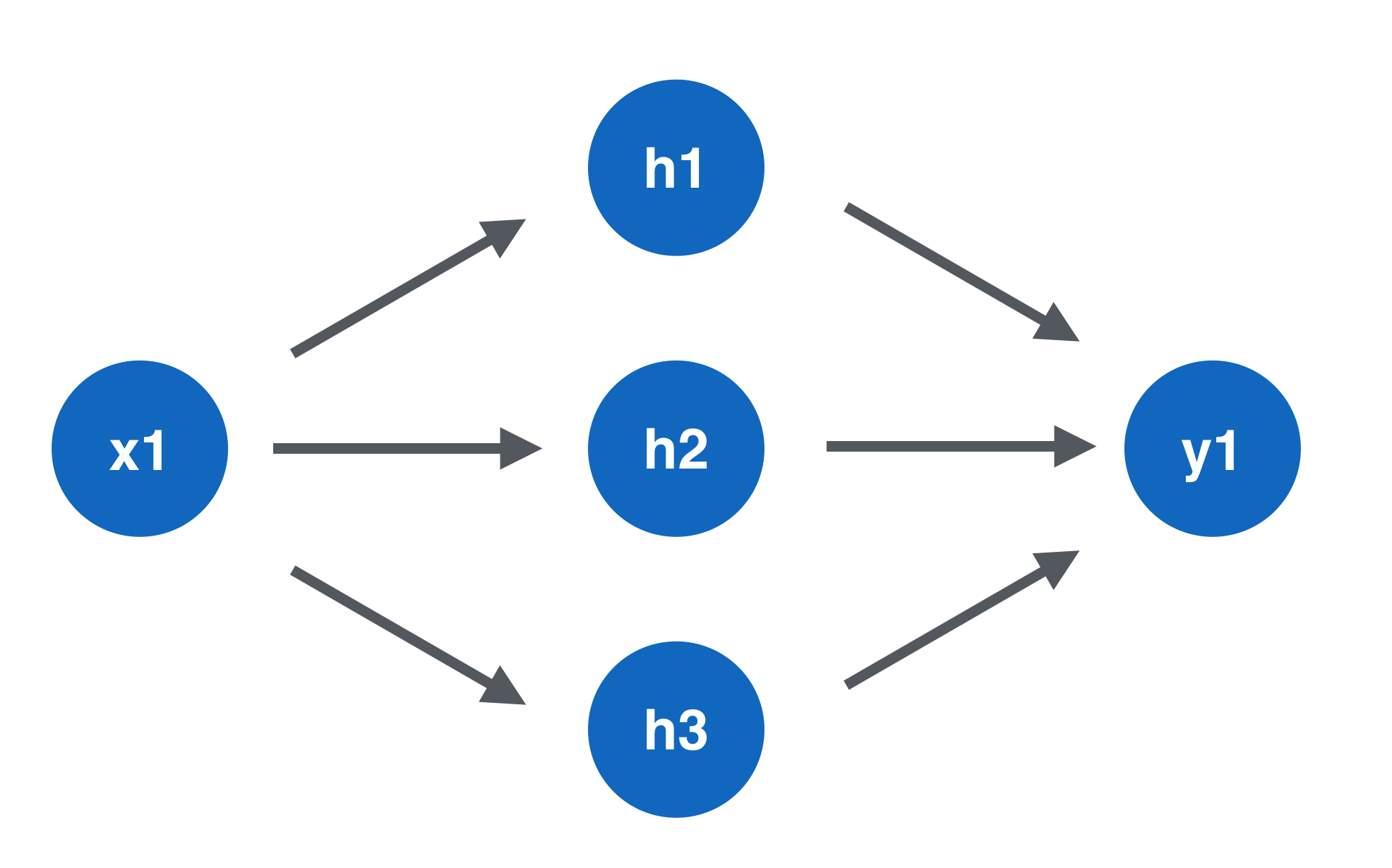
先ほどまで扱っていたユニットが連結しました。
今回はフィードフォワード型と呼ばれる結合をしたニューラルネットを対象にします。
青丸が、ユニットを表しています。
xが出力層、hが隠れ層、yが出力層を示しています。
この例だと、1->3->1のニューラルネットですね。
入力層は、特徴量の数が複数の場合、x2, x3...とその数だけ増やします。
出力層は、予測対象によってユニットの個数と活性化関数が異なります。
例えば、株価や気温等の実数値を予測する場合などでは、線形関数のユニットを一つにしますし、スパムメール判定等の2値分類問題だと、シグモイド関数のユニットを一つ、記事/音楽ジャンル分類等の多値分類だとソフトマックス関数のユニットを、分類対象の数だけ用意します。
隠れ層は、入力層での特徴量を別の特徴量にマッピングする機能があるようです。
どれだけのユニットを用意すれば十分なのかは、問題によって異なるため、一概に定めることが出来ません。
入力層から順に、ユニットが出力を行い、それが次の層に向かい、入力として受け取り、ユニットが出力を行い...ということを出力層のユニットが終えるまで繰り返します。
次の例のように、ニューラルネットの重みネットワークを表現することにします。
[{:activate-fn :sigmoid :units [{:bias -2 :w-list [2]}
{:bias 1 :w-list [3]}
{:bias -3 :w-list [-4]}]}
{:activate-fn :linear :units [{:bias -5 :w-list [1 -2 3]}]}]
上の例では、1->3->1のニューラルネットを表しています。
{:bias -2 :w-list [2]} 等が具体的な、あるユニットの持つ、重みやバイアスだと思ってください。
また、{:activate-fn :sigmoid :units [...]} 等が一つの層を表していると思ってください。
ニューラルネットワークの入力と出力
(defn network-output [w-network x-list]
(loop [w-network w-network, input-list x-list, acc [x-list]]
(if-let [layer (first w-network)]
(let [{activate-fn :activate-fn units :units} layer
output-list (map (fn [{bias :bias w-list :w-list}]
(unit-output input-list w-list bias activate-fn))
units)]
(recur (rest w-network) output-list (cons output-list acc)))
(reverse acc))))
難しく見えますが、気のせいです!
入力層->隠れ層->出力層、の順番に先ほどのunit-outputを一つずつ計算しているだけです。
大きなloopが層を、mapがその層のユニット1つずつに対する計算を行っています。
出力層の出力が、ニューラルネットの出力として扱われます。
さて、試してみましょう。
(network-output
[{:activate-fn :sigmoid :units [{:bias -2 :w-list [2]}
{:bias 1 :w-list [3]}
{:bias -3 :w-list [-4]}]}
{:activate-fn :linear :units [{:bias -5 :w-list [1 -2 3]}]}]
[2])
=> ([2] (0.8807970779778823 0.9990889488055994 1.670142184809518E-5) (-6.117330715367772))
さて、ここまでで重みやバイアス等のパラメータを渡したら、ニューラルネットによって予測/分類ができるようになりました。
次からは、それらパラメータをどのように学習するかという話題に移ります。
ニューラルネットによる学習
ニューラルネットの重みを求める段階までやってきました。
重みは、予め用意した入力と正解の出力のペアを用意しておくことで、求めることができます。
教師あり学習としての枠組みなので、ナイーブベイズやSVMと必要な情報は全く同じですね。
ニューラルネットは誤差逆伝播と呼ばれる手法によって、学習を行います。
早速取り上げてみましょう。
誤差逆伝播(バックプロパゲーション)
誤差逆伝播には大きく分けて2つの過程があります。
1. 予測の結果と正解の間での誤差に対し、それぞれのユニットが誤差に対してどれだけの責任があるのかを求める
2. 責任の大きさの分だけ、それぞれのユニットは重みとバイアスを修正する
この過程を出力層->中間層のように、上の層から下の層に繰り返していきます。
先程までのニューラルネットの出力とは計算の順番が逆ですね。
誤差をニューラルネットの出力と逆方向に伝播するので、誤差逆伝播の呼名がついているようです。
1.については、まず正解から予測の結果を引きます。
また、ユニットの出力で見てきたように、活性化関数を経由した出力による誤差であるため、活性化関数の微分値を考慮します。
シグモイド関数、線形関数の微分は次のようにコードで表現出来ます。
(defn derivative-value [unit-output activate-fn]
(condp = activate-fn
:sigmoid (* (sigmoid unit-output) (- 1 (sigmoid unit-output)))
:linear 1))
出力層でのユニットの責任の量は、誤差と活性化関数の微分にユニットの出力を与えたものを掛け合わせることで計算できます。
中間層でのユニットの責任の量は、出力層におけるユニットの影響もあるため、もう少し複雑です。
中間層の任意のユニットは、接続している出力層のすべてのユニットの責任の量について重み付けしたものを足しあわせ、その中間層のユニットの活性化関数の微分にそのユニットが出力した値を入れたものとを掛けあわせた値が、その中間層の責任の量となります。
後述のコードで理解したほうが簡単そうですね。
2.については、1.で求めた誤差の責任の量によって、パラメータの更新を行います。
ある重みについて更新する際には、責任の量以外の2つのパラメータとして、重みの対象となる下層の入力の大きさと、学習率というものがあります。
これらは掛け合わせた上で、元の重みの値から減算するだけなので簡単です。
ちなみにバイアスの更新は、元のバイアス値から責任の量*学習率を引くだけです。
それでは誤差逆伝播のコードを掲載します。
(defn back-propagation [w-network training-x training-y learning-rate]
(let [reversed-w-network (reverse w-network)
reversed-output-net (reverse (network-output w-network training-x))]
(loop [reversed-w-network reversed-w-network
reversed-output-net reversed-output-net
delta-list (mapv #(* (- %2 %1)
(derivative-value %2 (:activate-fn (first reversed-w-network))))
training-y (first reversed-output-net))
acc []]
(if-let [w-layer (first reversed-w-network)]
(let [output-layer (first reversed-output-net)
input-layer (first (rest reversed-output-net))
updated-w-list {:units (map (fn [{bias :bias w-list :w-list} delta]
{:w-list (map (fn [w input]
(- w (* learning-rate delta input)))
w-list input-layer)
:bias (- bias (* learning-rate delta))})
(:units w-layer) delta-list)
:activate-fn (:activate-fn w-layer)}]
(recur (rest reversed-w-network)
(rest reversed-output-net)
(map-indexed (fn [index unit-output]
(let [connected-w-list (map #(nth (:w-list %) index) (:units w-layer))]
(* (->> (mapv #(* %1 %2) delta-list connected-w-list)
(reduce +))
(derivative-value unit-output (:activate-fn (first (rest reversed-w-network)))))))
input-layer)
(cons updated-w-list acc)))
acc))))
端折ったらもっと小さく記述できたのですが、コードの長さよるも計算の流れを追跡しやすいことを目的にしていたので、大きくなってしまいました。
とはいえ、この関数の本質は既に述べたように、1.責任の量の計算と2.重みとバイアスの更新です。
要所だけ取り上げてみます。
引数のtraining-xが入力層の出力にあたる部分、training-yが正解ラベルです。
loopで層ごとに計算を行っています。
delta-listがその層における、それぞれのユニットの責任の量を表しています。
updated-w-listが、その層で更新されたそれぞれのユニットの重みとバイアスの値を表しています。
connected-w-listが上層のユニットでの、中間層のこのユニットに対して接続のある部分を表しています。
また、この関数の出力は、すべてのユニットの重みとバイアスが更新された新しいニューラルネットの情報です。
では、計算してみましょうか。
(back-propagation
[{:activate-fn :sigmoid :units [{:bias -2 :w-list [2]}
{:bias 1 :w-list [3]}
{:bias -3 :w-list [-4]}]}
{:activate-fn :linear :units [{:bias -5 :w-list [1 -2 3]}]}]
[2]
[5]
0.05)
=> ({:units ({:w-list (2.1167248411922994), :bias -1.9416375794038503}
{:w-list (2.9979761540232905), :bias 0.9989880770116454}
{:w-list (-3.9999442983612816), :bias -2.999972149180641}),
:activate-fn :sigmoid}
{:units ({:w-list (1.4896056204504848 -1.4446398871029504 3.000009283761505),
:bias -4.444133464231611}),
:activate-fn :linear})
重みとバイアスの値が更新された、同じ形式の重みネットワークが出力されていることが確認できますね。
ニューラルネットの初期化
誤差逆伝播ができるようになりましたが、そもそも最初のニューラルネットの重みって何を用意すればいいのでしょうか?
ニューラルネットの重みの初期化処理として、乱数を与える方法が主流です。
与える乱数の範囲などにコツがあるらしいですが、ちゃんと調べてないので、また次以降の機会に紹介します。
(defn init-w-network [network-info]
(loop [network-info network-info, acc []]
(if-let [layer-info (first (rest network-info))]
(let [{n :unit-num a :activate-fn} layer-info
{bottom-leyer-n :unit-num} (first network-info)]
(recur (rest network-info)
(cons {:activate-fn a
:units (repeatedly n (fn [] {:bias (rand) :w-list (repeatedly bottom-leyer-n rand)}))} acc)))
(reverse acc))))
では、使ってみましょう!
(init-w-network [{:unit-num 1 :activate-fn :linear}
{:unit-num 3 :activate-fn :sigmoid}
{:unit-num 1 :activate-fn :linear}])
=> ({:activate-fn :sigmoid,
:units ({:bias 0.7732887809599917, :w-list (0.9425957186019741)}
{:bias 0.9502325742816429, :w-list (0.53860907921595)}
{:bias 0.6318880361706507, :w-list (0.6481147062091354)})}
{:activate-fn :linear,
:units ({:bias 0.3295752168787115, :w-list (0.9050385230268984 0.5103400587715446 0.4064520926825912)})})
1->3->1という形式のフィードフォワード形式のネットが生成できました。
単純にrandを叩いているだけなので、0~1の値で乱数が生成されています。
また、それぞれの層ごとに活性化関数についても指定しています。
ちなみに、実は入力層の活性化関数は指定する必要がないです、ユニットの個数は必要です。
さて、ニューラルネットの初期化もでき、誤差逆伝播もできるようになったので、次はデータセット全体に対して学習を行ってみましょう。
データセット全体に対する学習
上記で既に作成した誤差逆伝播のコードは、一つのトレーニングペアに対するものでした。
これを、トレーニングデータの数だけ繰り返してやりましょう!
(defn train [w-network training-list learning-rate]
(loop [w-network w-network, training-list training-list]
(if-let [training (first training-list)]
(recur (back-propagation w-network (:training-x training) (:training-y training) learning-rate) (rest training-list))
w-network)))
トレーニングデータ一個ずつに対して誤差逆伝播を行う方法は確率的勾配降下法と呼称されています。
勾配法自体はニューラルネットに限定されるものではなく、最適化のために活用される手法です。
勾配法関連の話題は、次のリンクがわかりやすく、かつ上手くまとまっていると思います。
また、次のリンクに、ニューラルネット重み最適化アルゴリズムがまとまっています。
他にも、ある程度のまとまりにしてからまとめて更新する、ミニバッチと呼ばれる手法があったりします。
この周辺はちゃんと調べきれていないのですが、並列処理などでいいことがあったりするのでしょうかね。
最後に、データセット全体に対する学習の単位をエポックと呼称するらしいです。
この記事の後半でも、この用語を使っていこうと思います。
学習データとニューラルネットの誤差
さて、ニューラルネットが学習をできるようになりましたが、本当に学習できているんでしょうか?
データセット全体に対して、ある段階でのニューラルネットによって、どれだけ誤差が生じているかを示す関数が必要ですね。
今回は、予測対象が量的データなので、二乗誤差の和を用います。
ちなみに、クラス分類等の質的データを予測対象とする場合にはクロスエントロピーを用いるのが一般的みたいです。
(defn sum-of-squares-error
[w-network training-list]
(loop [training-list training-list, acc 0]
(let [{training-x :training-x training-y :training-y} (first training-list)]
(if (and training-x training-y)
(let [output-layer (first (reverse (network-output w-network training-x)))
error (->> (mapv #(* 0.5 (- %1 %2) (- %1 %2)) output-layer training-y)
(reduce +))]
(recur (rest training-list) (+ error acc)))
acc))))
training-listは学習データセット全体の入力と期待される出力のペアのリストです。
簡単に示すと、
[{:training-x x1 :training-y y1], {:training-x x2 :training-y y2}, ... ,{:training-x xn :training-y yn}]
というペアです。
ちなみにx,yは共に、具体的な数値などではなく、それらが含まれるベクトルですのでご注意ください。
この関数の結果の数値が小さければ小さいほど、誤差が少ないことを表しています。
学習の打ち切り
トレーニングペア全体に対して誤差逆伝播を繰り返すことができるようになりましたし、ニューラルネットとトレーニングデータセット全体との間に生じる誤差も求めることができるようになりました。
では、学習はどこまで行えばいいのでしょうか?
一般的には、エポック数で条件付ける方法と、誤差の値が一定以下の値になった時というように条件付ける方法があるようです。
今回は、エポック数で条件付けましたが、どちらでも大丈夫でしょう。
大切なのは、ニューラルネットの出力とトレーニングデータ間での最終的な誤差です。
では、ニューラルネットの学習を行う関数を次に示します。
(defn training-loop [w-network training-list learning-rate epoc]
(loop [w-network w-network, epoc epoc]
(if (> epoc 0)
(let [w-network (train w-network (shuffle training-list) learning-rate)
error (sum-of-squares-error w-network training-list)]
(println (str "epoc=> " epoc "\nw-network=> " w-network "\nerror=> " error"\n"))
(recur w-network (dec epoc)))
w-network)))
エポックごとに、その瞬間の学習されているニューラルネットと学習データ全体との誤差を出力しています。
また、エポック毎に学習データの順番をシャッフルしています。
どこからの知見かは失念してしまいましたが、確率的勾配法降下法においては、学習データのシャッフルはしておいた方がいいらしいです。
さて、準備ができましたね。
次に、実際に関数が近似できるのかどうかを見ていきましょう。
ニューラルネットによる関数近似
実際に上記で作成したニューラルネットが上手く動いているのかどうかを試すために、関数近似を行ってみましょう。
次のサイトを参考にして、sin関数を近似してみましょうか。
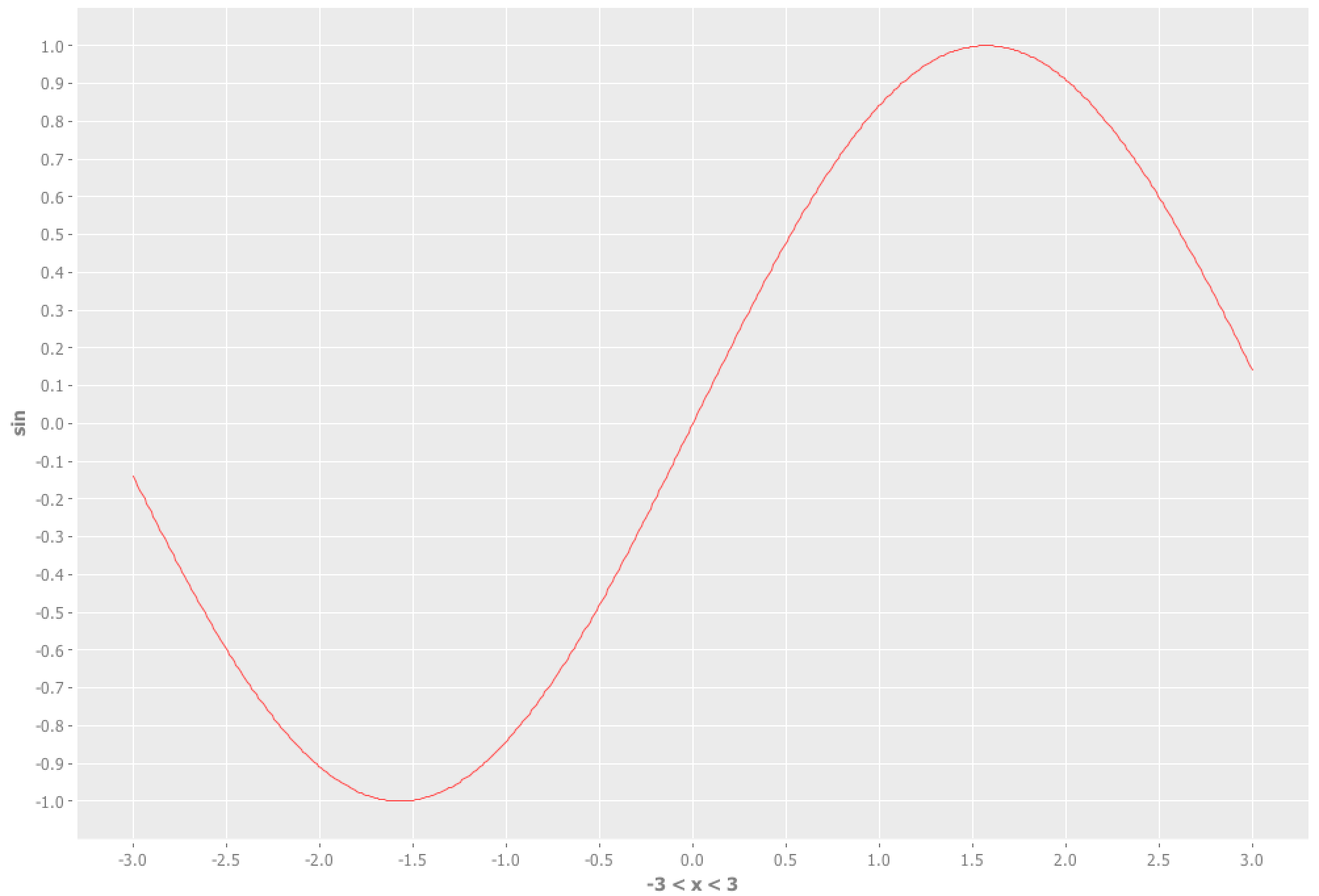
sin関数の-3〜3の範囲は、incanter活用すると次のコードでグラフが作成できます。
(use '[incanter core charts])
(view (function-plot sin -3 3))
さて、ここまで作ってきたニューラルネットを学習させてみましょう!
まず、sin関数の-3〜3までの範囲の教師データを作成します。
(def training-list-sin3 (map (fn[x]{:training-x [x] :training-y [(sin x)]}) (range -3 3 0.2)))
次に、学習させて、近似した関数を表示してみましょう。
(let [hidden-num 3
w-network (training-loop (init-w-network [{:unit-num 1 :activate-fn :linear}
{:unit-num hidden-num :activate-fn :sigmoid}
{:unit-num 1 :activate-fn :linear}]) training-list-sin3 0.05 10000)
nn-plot (-> (function-plot sin -3 3)
(add-function #(first (last (network-output w-network [%]))) -3 3))]
(loop [counter-list (range hidden-num), nn-plot nn-plot]
(if-let [counter (first counter-list)]
(let [nn-plot (-> nn-plot
(add-function #(nth (second (network-output w-network [%])) counter) -3 3)
(set-stroke-color java.awt.Color/gray :dataset (+ 2 counter)))]
(recur (rest counter-list) nn-plot))
(view nn-plot))))
学習率を0.05、エポックを10000に指定しています。
epoc=> 10000
w-network=> ({:units ({:w-list (0.7762071114644875), :bias 0.934202087725845} {:w-list (0.71259848242352), :bias 0.3923585053865499} {:w-list (0.3531967795051996), :bias 0.3666245768857553}), :activate-fn :sigmoid} {:units ({:w-list (-0.06241386610995453 0.5017590975297447 0.04674924183291745), :bias -0.06559857533268038}), :activate-fn :linear})
error=> 6.49481052309475
epoc=> 9999
w-network=> ({:units ({:w-list (0.7635313222792359), :bias 0.9381324593508904} {:w-list (0.8173345796110145), :bias 0.367435725062919} {:w-list (0.3590346056434103), :bias 0.3641435270530943}), :activate-fn :sigmoid} {:units ({:w-list (0.029020665080020568 0.6253818214957477 0.07647175632503583), :bias -0.1840109162914652}), :activate-fn :linear})
error=> 5.576633287536219
...
epoc=> 1
w-network=> ({:units ({:w-list (1.3149880622798489), :bias 3.7004741564729247} {:w-list (1.0277198514604684), :bias -0.07311527945779911} {:w-list (1.1943472243476663), :bias -3.337095923742682}), :activate-fn :sigmoid} {:units ({:w-list (-3.541177540453866 4.9350159965992235 -3.9634510517986725), :bias 1.213416934866844}), :activate-fn :linear})
error=> 3.550693188617979E-5
途中を端折りましたが、誤差がだんだん減っていくことが確認できると思います。
最後のエポックでの誤差は、E-5が最後についているので、結構小さい値ですね。
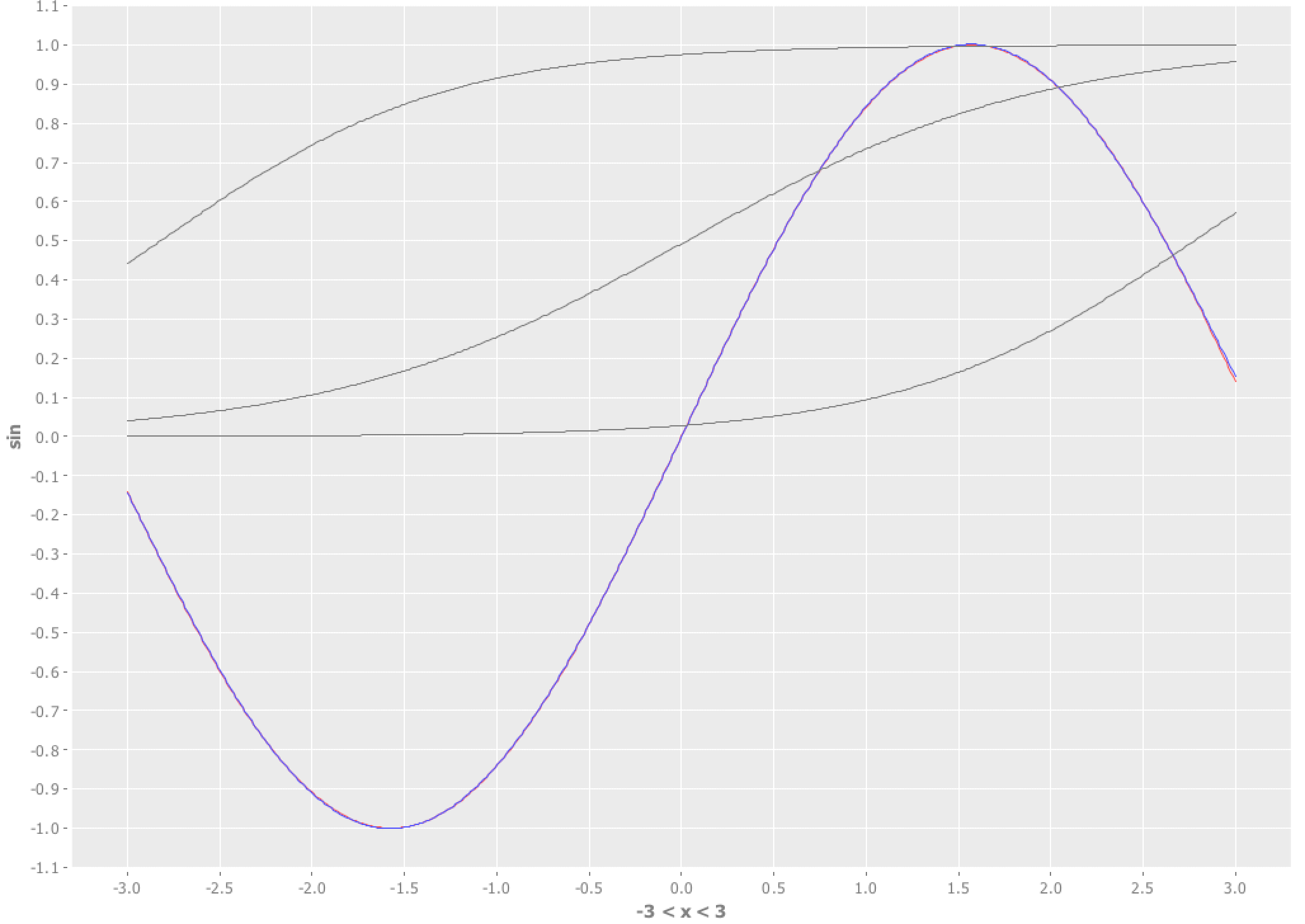
学習が終わると、次のようにグラフでの結果が表示されます。
一見よくわからないですが、よく見ると赤線が青線に塗りつぶされています。
赤線がsin関数、青線が近似したニューラルネットの出力値です。
視覚的には、とてもよく近似できていると言えるのではないでしょうか。
また灰色の線が隠れ層の出力結果を表しています。
各ユニットの出力は、最終的にはシグモイド関数による出力なので、0~1の間にしか灰色の線は存在していません。
これらが重み付けで足され、バイアスで引いた値のラインが青色になるということですね。
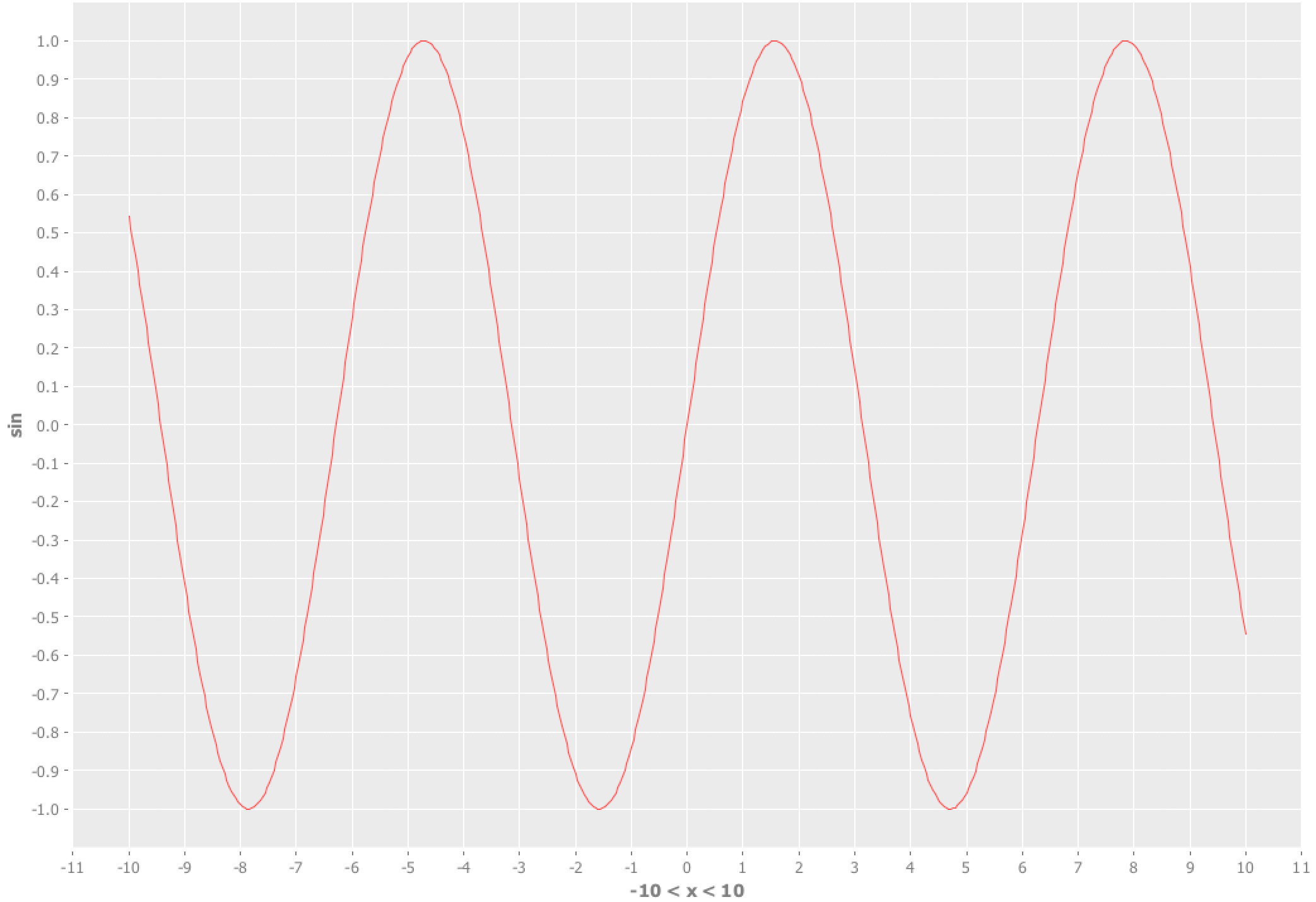
次に、sin関数の-10~10の範囲で試してみましょう。
(use '[incanter core charts])
(view (function-plot sin -10 10))
山と谷が増えましたね。
先ほどと同じ形式のニューラルネットで近似できるのでしょうか?
まず、学習データを作ります。
(def training-list-sin10 (map (fn[x]{:training-x [x] :training-y [(sin x)]}) (range -10 10 0.2)))
次に学習データを変更して、1->3->1のニューラルネットで学習してみましょう。
(let [hidden-num 3
w-network (training-loop (init-w-network [{:unit-num 1 :activate-fn :linear}
{:unit-num hidden-num :activate-fn :sigmoid}
{:unit-num 1 :activate-fn :linear}]) training-list-sin10 0.05 10000)
nn-plot (-> (function-plot sin -10 10)
(add-function #(first (last (network-output w-network [%]))) -10 10))]
(loop [counter-list (range hidden-num), nn-plot nn-plot]
(if-let [counter (first counter-list)]
(let [nn-plot (-> nn-plot
(add-function #(nth (second (network-output w-network [%])) counter) -10 10)
(set-stroke-color java.awt.Color/gray :dataset (+ 2 counter)))]
(recur (rest counter-list) nn-plot))
(view nn-plot))))
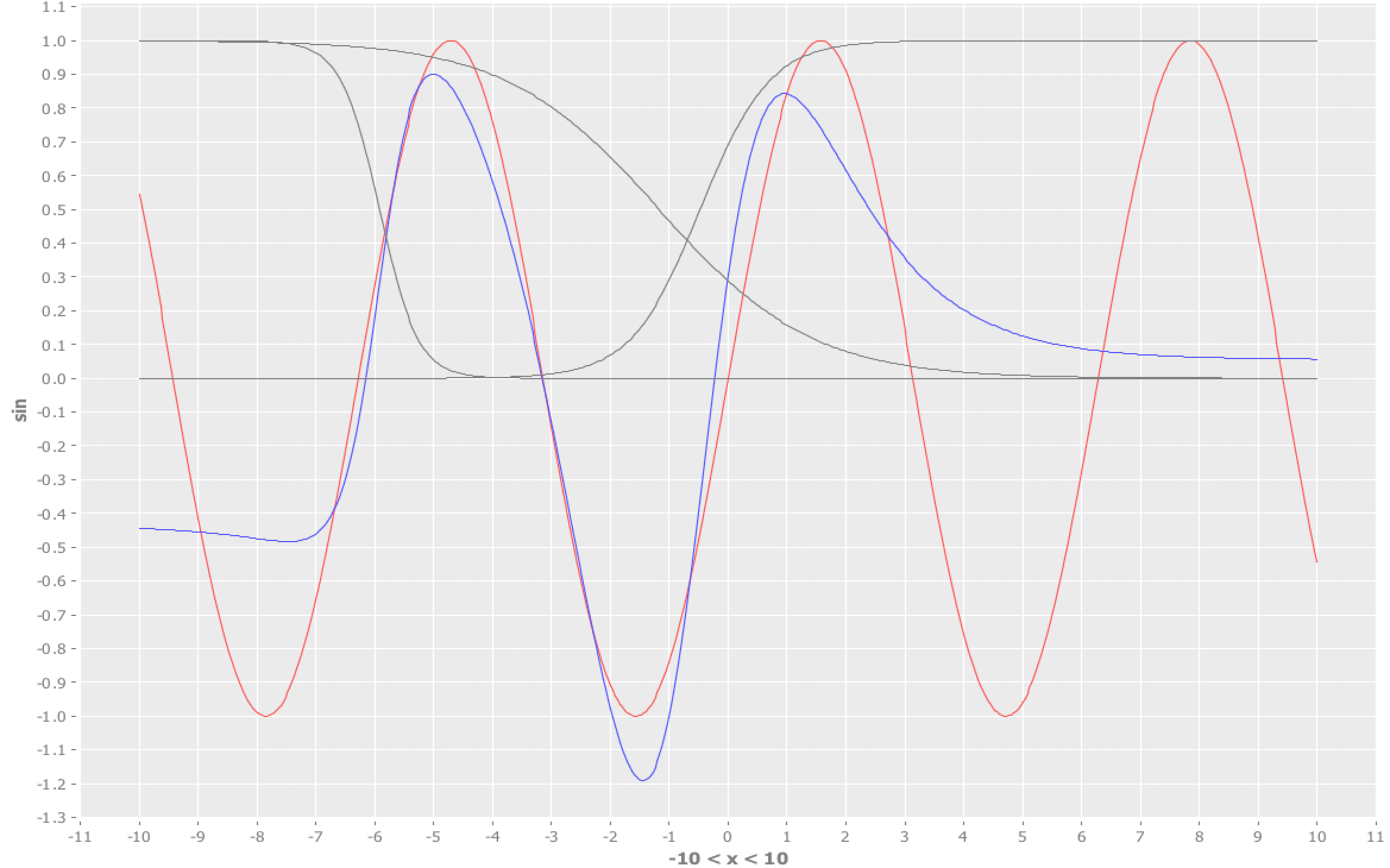
そして結果がこちら。
あれ、だめだめですね。
誤差も11~13付近をいったりきたりで、0に全然近づきません。
グラフからも、2つの山と一つの谷に関しては頑張ろうとした形跡が見えますが、それ以外が雑ですね。
隠れ層の出力は、(交差していて分かりにくいですが)上がりっぱなしか下がりっぱなしにしかならないので、学習回数を増やしてもフィットできなさそうです。
それでは、適当に隠れ層のユニット数を増やしてみましょうか!
(let [hidden-num 10
w-network (training-loop (init-w-network [{:unit-num 1 :activate-fn :linear}
{:unit-num hidden-num :activate-fn :sigmoid}
{:unit-num 1 :activate-fn :linear}]) training-list-sin10 0.05 10000)
nn-plot (-> (function-plot sin -10 10)
(add-function #(first (last (network-output w-network [%]))) -10 10))]
(loop [counter-list (range hidden-num), nn-plot nn-plot]
(if-let [counter (first counter-list)]
(let [nn-plot (-> nn-plot
(add-function #(nth (second (network-output w-network [%])) counter) -10 10)
(set-stroke-color java.awt.Color/gray :dataset (+ 2 counter)))]
(recur (rest counter-list) nn-plot))
(view nn-plot))))
先ほどのコードの、hidden-numを10に変更しただけですね、隠れ層のユニットが10個ということです。
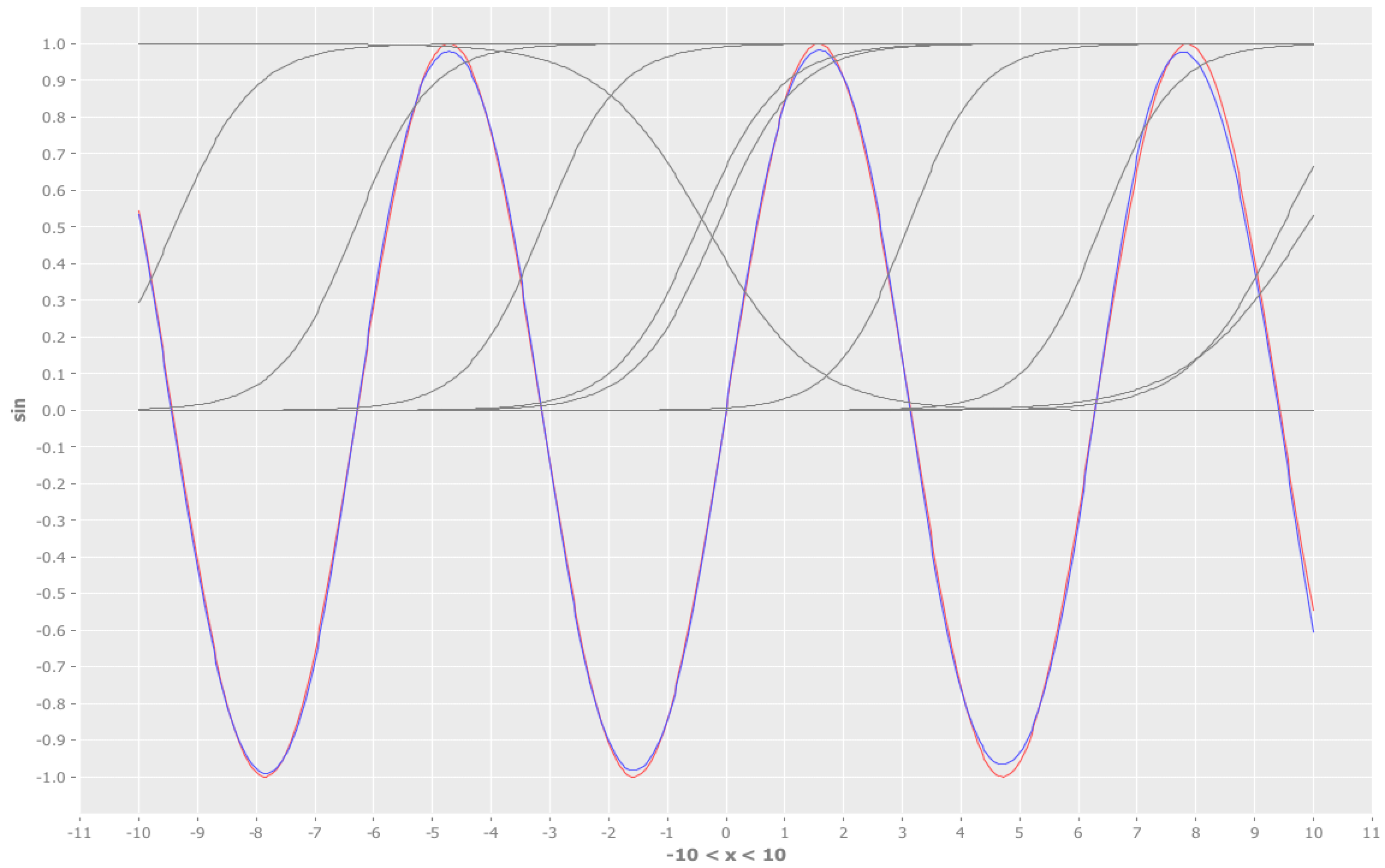
さて、結果は次のようになりました。
いい感じに近似できてるのではないでしょうか。
隠れ層の数が十分でないと、ニューラルネットも本来の力が発揮できないことがわかりましたね。
ニューラルネットで教師あり機械学習をする際にも、予め教師データを散布図などで確認して、データの性質を意識しておくという、一般的な手続きを経ることが大切ですね。
ハマったところ
ここまでさくっとコードを示してきましたが、ちゃんと色々な箇所でハマっていました。
sin関数の近似を行うときに、ニューラルネットの出力層をシグモイド関数にしていた
確か、誤差逆伝播の際にめちゃくちゃになった気がします。
ここにハマったせいで、お昼ごはんを食べそこねたので、出力層の活性化関数がなんでもいいというわけではない、ということが身に染みてわかりました。
sin関数の近似の際、-10~10でやっていたら隠れ層が足りていなかった
既に述べた参考にしたサイトでは1->3->1層のニューラルネットを-3~3の範囲でやっていたのですが、なんとなく-10~10の範囲でやってみたら全然近似が出来なく、誤差逆伝播のコードを間違えていたと思い込んでいました。
おかげで、隠れ層の数が重要だということもよくわかりました。
まとめ
この記事では、Clojureを使って、0からニューラルネットを構築しました。
ユニットやニューラルネットワークの出力の計算をコードで示し、誤差逆伝播によるニューラルネットの重み学習についても扱いました。
最後に、sin関数が近似できるかどうかを試すことで、隠れ層の挙動について確認し、用意する隠れ層の数、ひいては近似する対象のデータの性質を理解することが大切であることを見てきました。
最後に、gistに今回用いたコードの全体を掲載しておこうと思います。
次はRNNか、テキストを扱うフィードフォワードのニューラルネットでもやろうと思います。
追記: シンタックスハイライトの追加ありがとうございます!