勾配降下法は何に使う?#
勾配降下法は統計学や機械学習で多く使われています。特に機械学習というのは基本的に何かしらの関数を最小化(最大化)する問題を数値解析的に解くことに帰結する場合が多いです。(e.g. 最小二乗法 → 誤差の二乗和を最小化(参考)、ニューラルネットワークのパラメータ決定 etc...)
なので、基本的にはひたすら微分して0となるところを探す問題ですね、微分して0。で、その微分して0となる値は何か、をプログラムで解く場合に重要になるのがこの勾配降下法です。幾つか勾配法にも種類がありますがここでは最急降下法、確率的勾配降下法の2つを扱います。まずはイメージをつかむために1次元のグラフで確認していきたいと思います。
1次元の場合##
1次元の場合は、確率的という概念はなく、ただの勾配降下法になります。
(どういうことか、はのちほど)
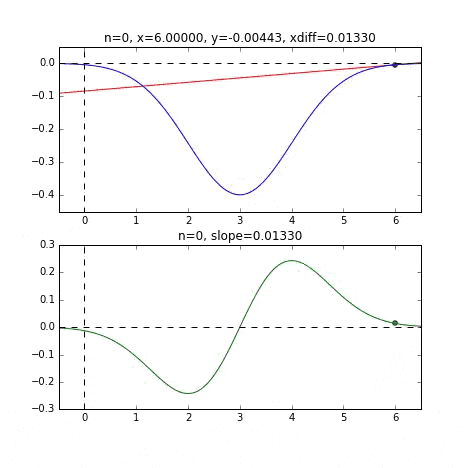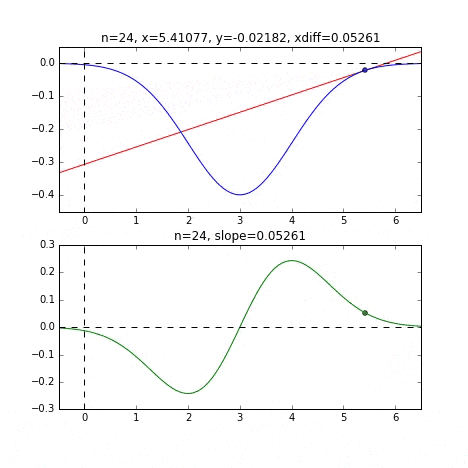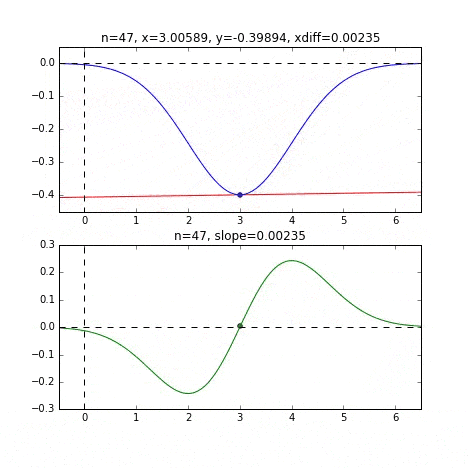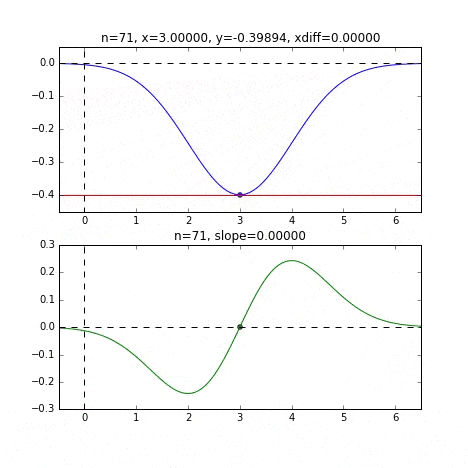
1次元の例は、正規分布をマイナスにしたものを使ってみます。$x_{init} = 0$と$x_{init} = 6$のグラフを例として作っています。対象となるグラフは正規分布の密度関数をマイナスして下向きにしたものを使いました。
初期値 = 0 のグラフ
グラフの端から始まって、ちゃんと一番小さいところ、最小値で収束していることがわかりますね。青い線のグラフが正規分布のマイナス版で、緑の線のグラフがその微分した値のグラフです。
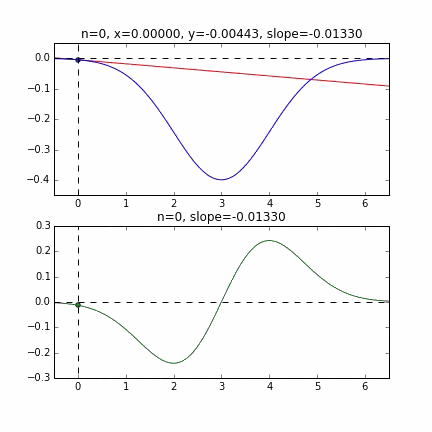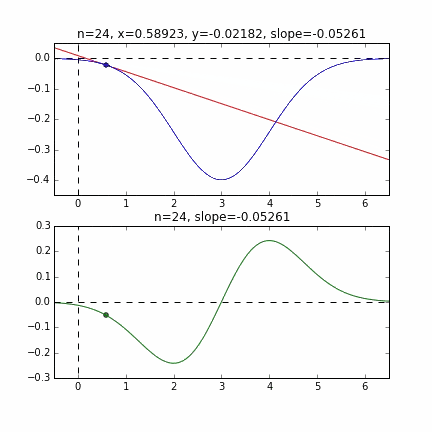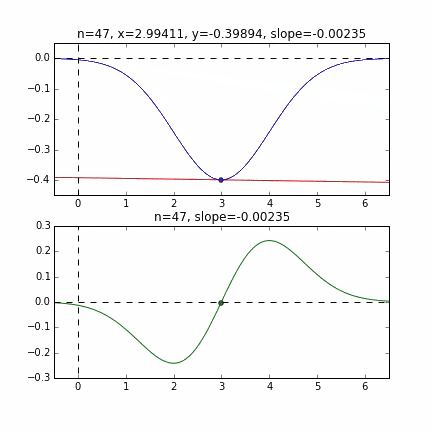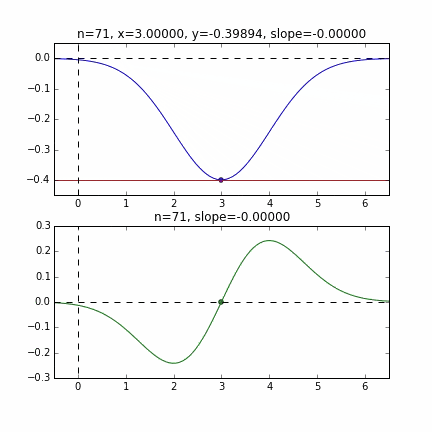
各点での傾きをベースに次の$x$の値を決め、またその位置での傾きを調べ次に降下して行く、という事を繰り返して最小値(本当は極小値)にたどり着きます。上の例だと、最小値に近ずくにつれ、傾きもなだらかになっていくので、1回のステップで進む量がだんだん小さくなり、それがある基準より小さくなるとストップする、というロジックを組んでいます。
これら2つのグラフを書いたコードはこちらです。
2次元の場合(2次関数)###
多次元の場合は次のステップに進む向きも考慮して降下していきます。ターゲットとなる関数により動きの特徴が変わるのですが、最初に2次関数 $Z=-3x^2-5y^2+6xy$ という関数を例にグラフを書いてみました。なんだかジグザグ動きながら頂点に向かって行く姿をみることができます。
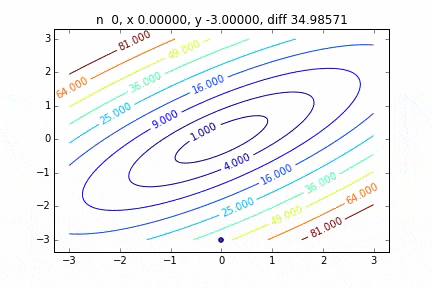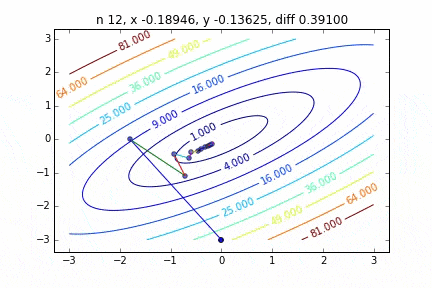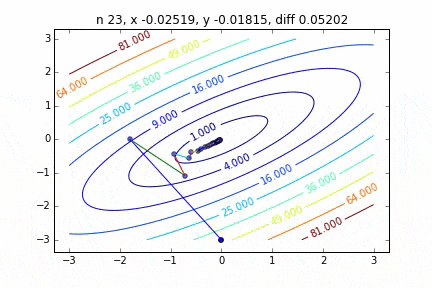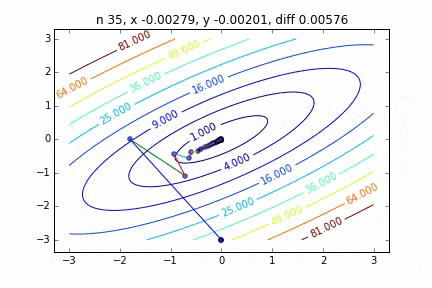
コードはこちら
2次元の場合##
2次元の場合(2次元正規分布)###
2次元正規分布(にマイナスをかけたもの)に対して最急降下法を適用するとジグザグ動かず、綺麗に最小値に降下していくことがわかりました。このあたりターゲット関数による収束の様子の違いについては今度調べてみたいと思います。
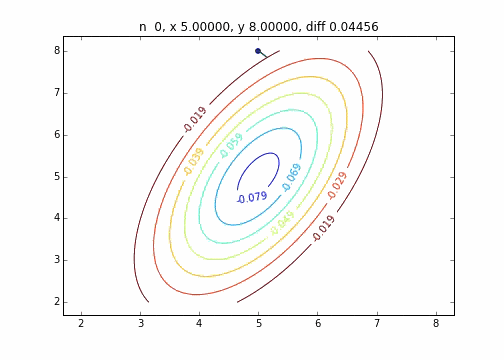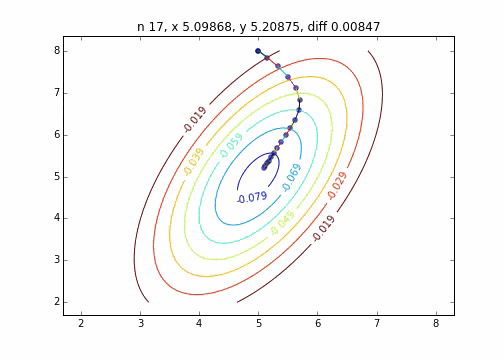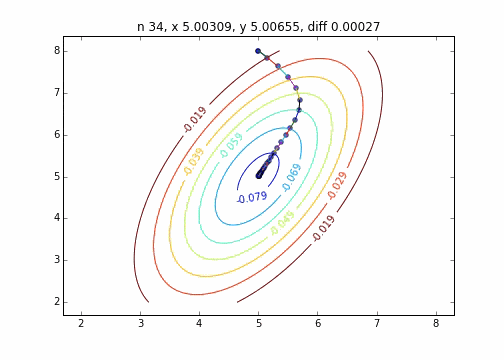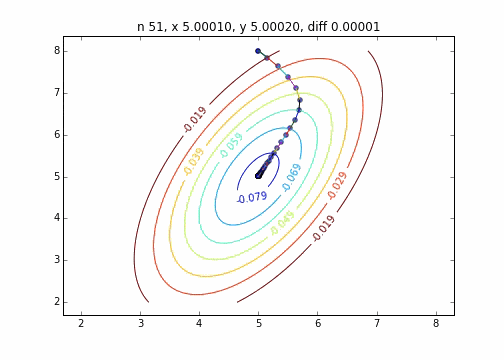
コードはこちら
最急降下法の仕組み###
最急降下法の仕組みは、まず最初にスタート地点を選び、その点での一番降下する傾きが大きいベクトル、つまり
\nabla f = \frac{d f({\bf x})}{d {\bf x}} = \left[ \begin{array}{r} \frac{\partial f}{\partial x_1} \\ ... \\ \frac{\partial f}{\partial x_2} \end{array} \right]
を利用して次のステップに行く方法です。上記のグラフでは、この勾配ベクトルに学習率$\eta$をかけたものを直線で表しています。
なので、
x_{i+1} = x_i - \eta \nabla f
というステップを収束するまで繰り返す、という処理を行っています。
確率的勾配降下法とは##
さて、次に確率的勾配降下法に移りたいと思います。
まず、対象とする関数ですが、以前回帰分析の説明で使った回帰直線の誤差関数を使って説明したいと思います。ちょっとその解釈を変えている部分(最尤法を使用)もあるので文末に補足として記載しておきます。
データは、
y_n = \alpha x_n + \beta + \epsilon_n (\alpha=1, \beta=0)\\
\epsilon_n ∼ N(0, 2)
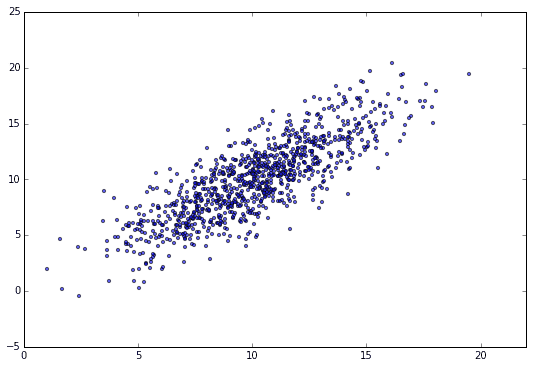
というN=1000個のデータセットを準備して、その回帰直線を求める例を使用します。散布図は以下の通りです。
誤差関数、
E({\bf w})=\sum_{n=1}^{N} E_n({\bf w}) = \sum_{n=1}^{N} (y_n -\alpha x_n - \beta)^2 \\
{\bf w} = (\alpha, \beta)^{\rm T}
の最小値を求めていきますが、まず勾配を計算するため、それぞれ$\alpha, \beta$で偏微分した勾配ベクトルを導出します。
\frac{\partial E({\bf w})}{\partial \alpha} = \sum_{n=1}^{N} \frac{\partial E_n({\bf w})}{\partial \alpha} =
\sum_{n=1}^N (2 x_n^2 \alpha + 2 x_n \beta - 2 x_n y_n )\\
\frac{\partial E({\bf w})}{\partial \beta} = \sum_{n=1}^{N}\frac{\partial E_n({\bf w})}{\partial \alpha} =
\sum_{n=1}^N (2\beta + 2 x_n \alpha - 2y_n)
なので、勾配ベクトルは
\nabla E({\bf w}) = \frac{d E({\bf w}) }{d {\bf w}} = \left[ \begin{array}{r} \frac{\partial E({\bf w})}{\partial \alpha} \\ \frac{\partial E({\bf w})}{\partial \beta} \end{array} \right] = \sum_{n=1}^{N}
\nabla E_n({\bf w}) = \sum_{n=1}^{N} \left[ \begin{array}{r} \frac{\partial E_n({\bf w})}{\partial \alpha} \\ \frac{\partial E_n({\bf w})}{\partial \beta} \end{array} \right]=
\left[ \begin{array}{r}
2 x_n^2 \alpha + 2 x_n \beta - 2 x_n y_n \\
2\beta + 2 x_n \alpha - 2y_n
\end{array} \right]
となります。
単回帰直線を求める問題なので、方程式として解いても良いのですが、これを確率的勾配降下法を用いて解くことを行っていきます。ここでN=1000個の全てのデータをすべて使うのではなく、ここからランダムサンプリングして取り出したデータに対して勾配を計算し、次のステップを決めるのがこの手法のキモです。
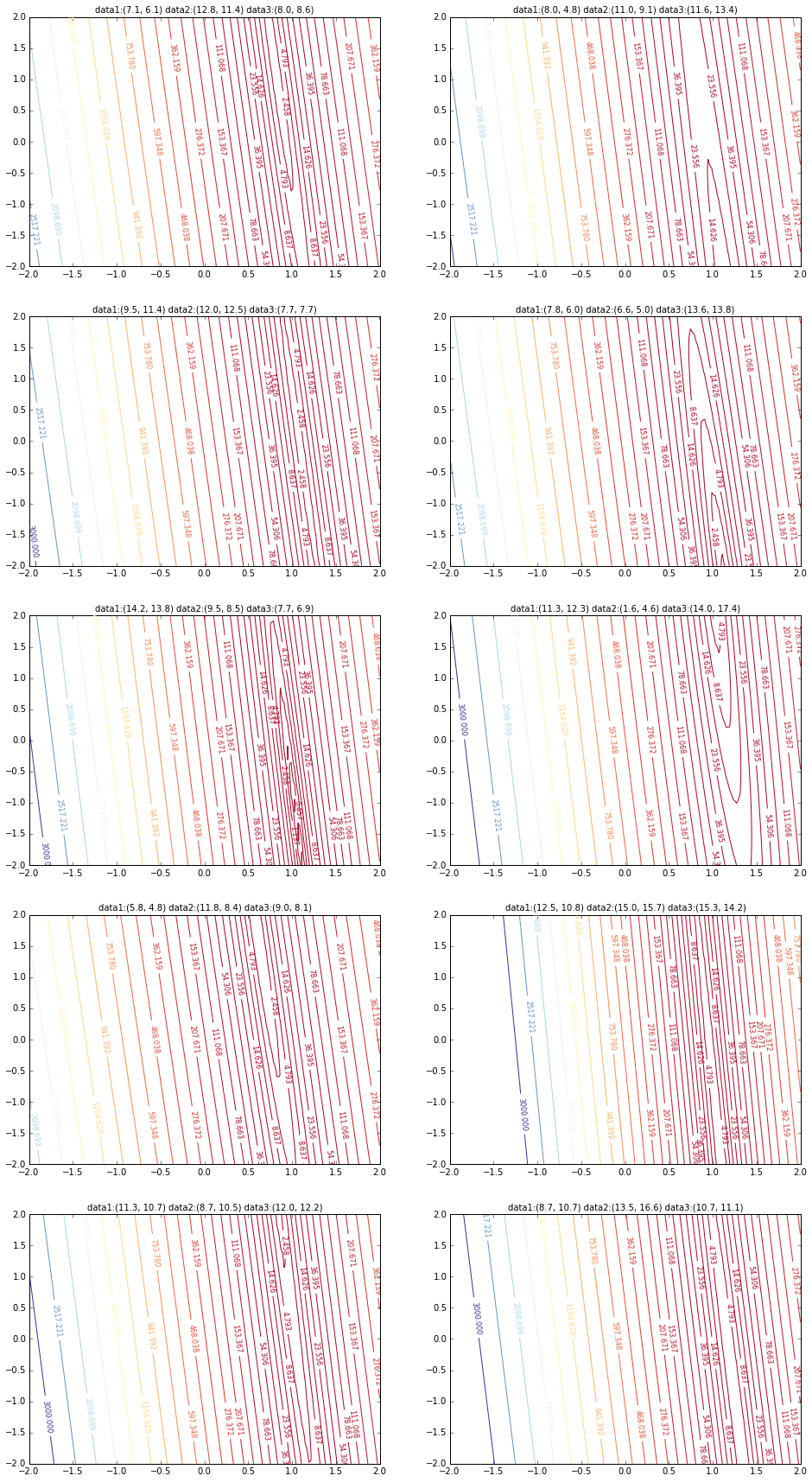
まずこのデータセットから20個ランダムに取り出してグラフにしてみます。横軸が$\alpha$、縦軸が$\beta$、Z軸が誤差$E(\alpha,\beta)$です。
なんとなくグラフの最小値が$\alpha=1, \beta=0$を中心に散らばっているかと思います。今回は1000個のデータからランダムに3つのデータをピックアップしてそれを元にこのグラフを書いています。
初期値を$\alpha=-1.5, \beta=-1.5$、学習率をイテレーション回数$t$の逆数に比例させ、さらにその地点での$E(\alpha, \beta)$の逆数もかけたものを使ってみました。この学習率と初期値の決め方について試行錯誤するしかないようなのですが、何か良い探し方をご存知の方がいれば教えてもらえると嬉しいです。ちょっと間違えるとあっという間に点が枠外に飛んで行って戻ってこなくなります(笑)
勾配を決める誤差関数が乱数に依存しているので毎回変化していることが見て取れます。回帰直線も最初は相当暴れていますが、だんだん大人しくなって収束していく様がわかると思います。
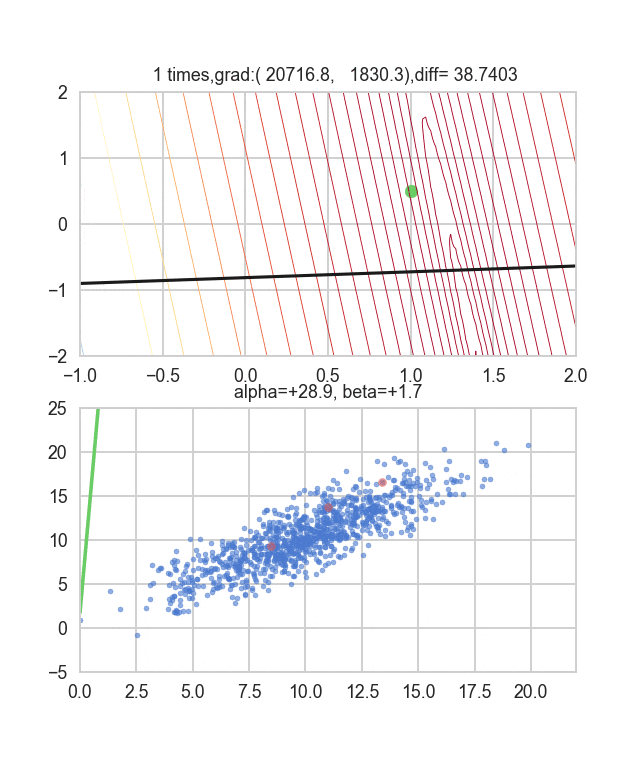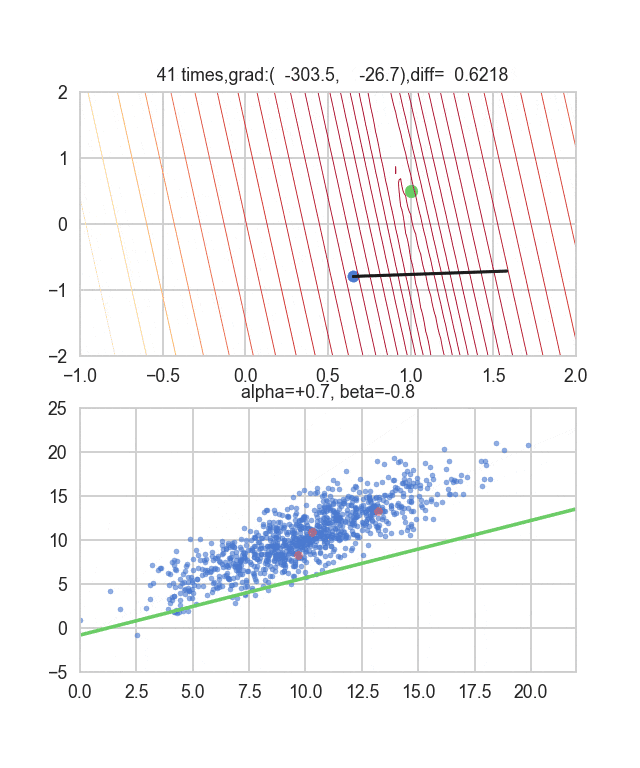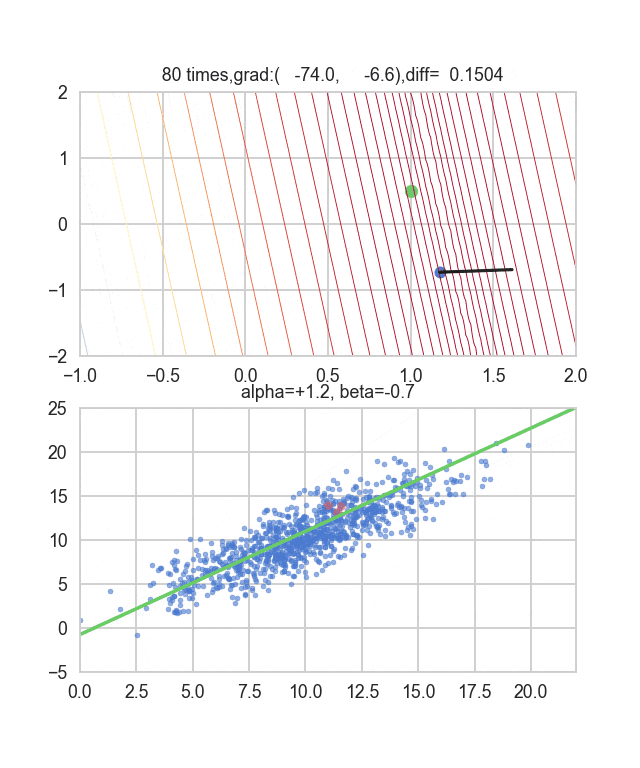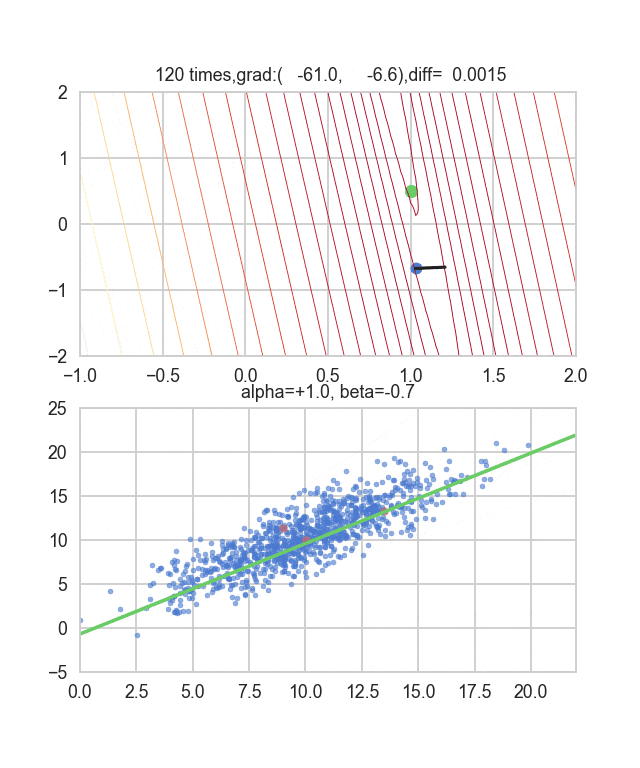
コードはこちら。
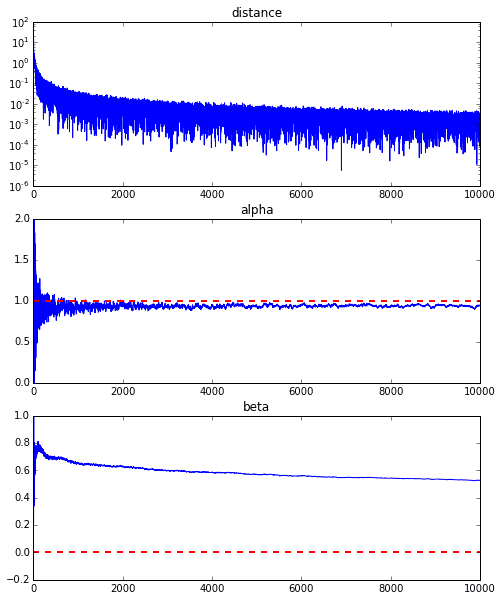
正直、上記のアニメーションの例は収束が良い方のものでして、下記に10000回繰り返した際の$\alpha$と$\beta$の収束具合をグラフにしたものを載せていますが、$\alpha$は真の値1に近づいているのですが、$\beta$は0.5のあたりで収束してしまい、真の値の0にこれ以上近づきそうにありません。
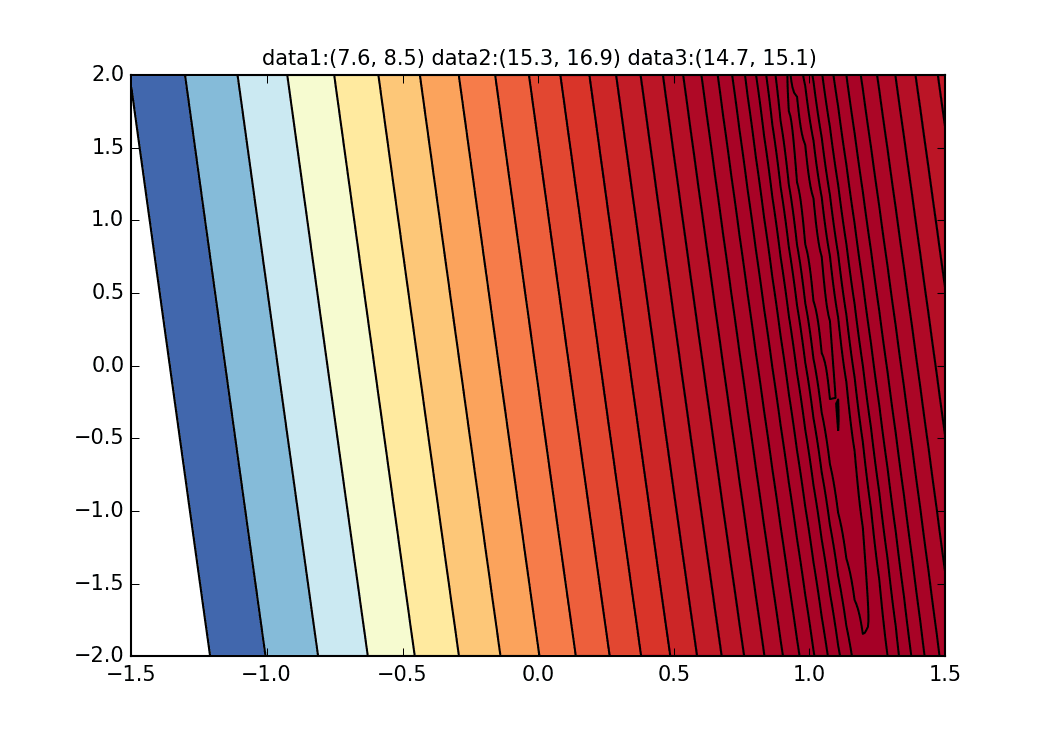
これはそもそもの今回の回帰直線の誤差関数の特性にあるようですが、下記のグラフを見てもらうとわかるように、$\alpha$については$\alpha=1$のあたりで大体曲線の最小値あたりに落ちています。しかし、縦のラインについてはとても緩やかな変化しかないため、なかなか縦の動きが出る勾配が出てこないのです。これが通常の最急降下法等であればこの曲面自体は変化しないので、谷に沿って緩やかに最小値を目指すのですが、そもそも毎回この曲面が変わってしまうことが原因で$\beta$方向の動きが生まれないようです。
さて、確率的勾配降下法についてイメージが湧きましたでしょうか?私はこのアニメーショングラフを描くことでイメージがつかめました。
この確率的勾配降下法のアニメーションを描くpythonコードはこちらにありますので、よければ試してみてください。
(補足)回帰直線のパラメータを最尤法で求める###
y_n = f(x_n, \alpha, \beta) + \epsilon_n (n =1,2,...,N)
つまり、誤差は
\epsilon_n = y_n - f(x_n, \alpha, \beta) (n =1,2,...,N) \\
\epsilon_n = y_n -\alpha x_n - \beta
で表すことができます。この誤差$\epsilon_i$を平均=0, 分散=$\sigma^2$の正規分布に従うとすると、誤差関数の尤度は
L = \prod_{n=1}^{N} \frac{1}{\sqrt{2\pi\sigma^2}} \exp \left( -\frac{\epsilon_n^2}{2\sigma^2} \right)
であり、対数をとると
\log L = -\frac{N}{2} \log (2\pi\sigma^2) -\frac{1}{2\sigma^2} \sum_{n=1}^{N} \epsilon_n^2
となり、パラメーター$\alpha, beta$に依存する項のみを取り出すと
l(\alpha, \beta) = \sum_{n=1}^{N} \epsilon_n^2 = \sum_{n=1}^{N} (y_n -\alpha x_n - \beta)^2
を最小化すれば良いことがわかります。
これを誤差関数として
E({\bf w})=\sum_{n=1}^{N} E_n({\bf w}) = \sum_{n=1}^{N} (y_n -\alpha x_n - \beta)^2 \\
{\bf w} = (\alpha, \beta)^{\rm T}
と表現します。