最近、機械学習、人工知能等が流行っておりその基盤となる統計学についての知識が重要となっていると思います。そこで、統計学の中でもその効果がわかりやすい回帰分析の原理についてPythonで計算したりグラフを書いたりしながら概念的に理解できることを目的として説明を試みたいと思います。
統計の専門家ではないので、もしご指摘・コメントありましたらぜひご連絡ください。数学的に厳密でない点もあると思いますが、ご容赦ください...
データセット###
まずはデータセットを入手します。
carsデータ###
このページではPythonを用いて説明を進めますが、使用するデータは統計解析ソフトRのなかにあるデータセットのcarsデータを用います。ここからcsvデータをダウンロードして利用してください。(ただし、このデータのDescriptionによると1920年代のデータのようなので、あくまでサンプルとしてのデータになりますね。)
この解説では"cars.csv"とし名前をつけて保存しているとして説明をします。
teble definition of cars data
[,0] index
[,1] speed numeric Speed (mph)
[,2] dist numeric Stopping distance (ft)
データの詳細説明はこちらにありますが、車のスピードと、そのスピードでブレーキを踏んだ時の停止距離を50セット集めたデータです。
Pythonの準備###
Pythonはバージョン2.7を使います。また、下記のライブラリがすでにインストールされていることを想定しています。
- Numpy
- Matplotlib
これらをインポートします。
import numpy as np
import matplotlib.pyplot as plt
データの読み込み###
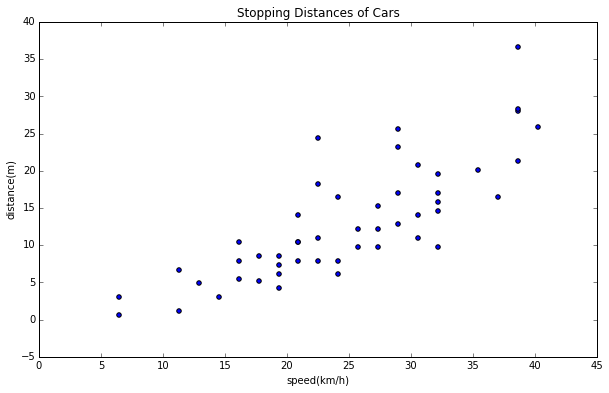
データを読み込んで、まずは散布図を描きます。データのイメージをつかむには、やはりグラフを描くのがわかりやすいですね。
さて、元データはマイルやら、フィートやら日本人になじみがない単位なので、メートル記載に単位変換を行います。
1フィート ≒ 0.3048メートル
1 mph ≒ 1.61 km/h
なので、下記の通りデータの単位変換を。
data= np.loadtxt('cars.csv',delimiter=',',skiprows=1)
data[:,1] = map(lambda x: x * 1.61, data[:,1]) # mph から km/h に変換
data[:,2] = map(lambda y: y * 0.3048, data[:,2]) # ft から m に変換
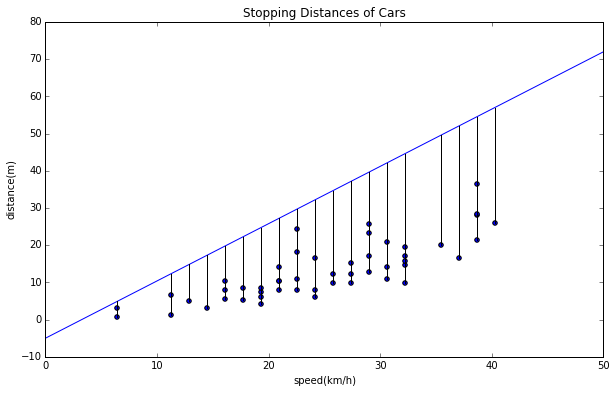
そしてそのデータをもとに散布図を描きます。
fig = plt.figure(figsize=(10,6))
ax = fig.add_subplot(111)
ax.set_title("Stopping Distances of Cars")
ax.set_xlabel("speed(km/h)")
ax.set_ylabel("distance(m)")
plt.scatter(data[:,1],data[:,2])
回帰分析とは
このデータを用いて回帰分析を使うと、あるスピードで走っている車が急ブレーキを踏んだ時にどれくらいの距離で完全にストップできるか、を求めることができます。つまり、
distance = \alpha * speed + \beta
のように1次方程式で表し求めることができるのです。これを単回帰分析といいます。(変数が1つなので、”単")この直線当てはめを1次近似と呼んだりします。$\alpha$は直線の傾き、$\beta$は切片の値ですね。この直線を近似直線と呼びましょう。
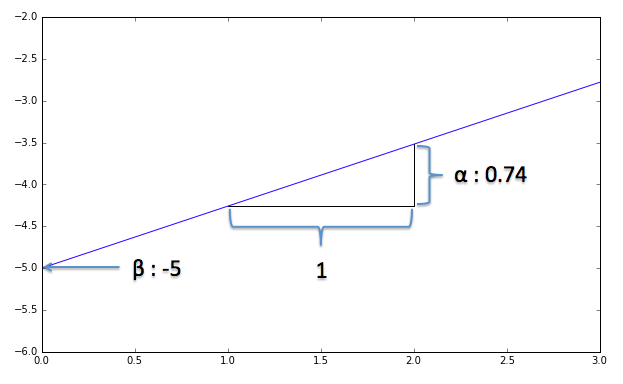
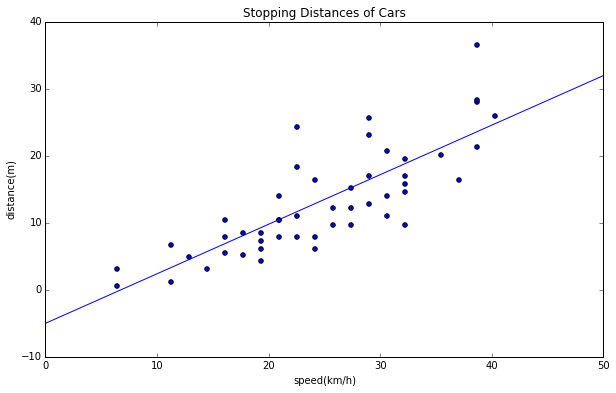
これを目視でなんとなく、直線を当てはめてみます。目視で当てはめたグラフが下記ですが、$\alpha$を0.74, $\beta$を−5としてみました。どうです?なんとなくこんな直線が当てはめられそうじゃないですか?
# y = 0.74x -5 の直線 ((0,-5),(50,32)を通る)
x = [0, 50]
y = [-5, 32]
plt.plot(x,y)
でも、あくまでこれは目視で当てはめてみただけなので、本当に最適な直線かがわかりません。では最適な$\alpha$と$\beta$を求めるやり方、最小二乗法を見ていきましょう。
最小二乗法##
最小二乗法とはなんでしょう、何を"最小"にするんでしょう?何を"二乗"するのでしょう?
何を最小にする?###
最小にするのは、直線とデータの誤差なんです。
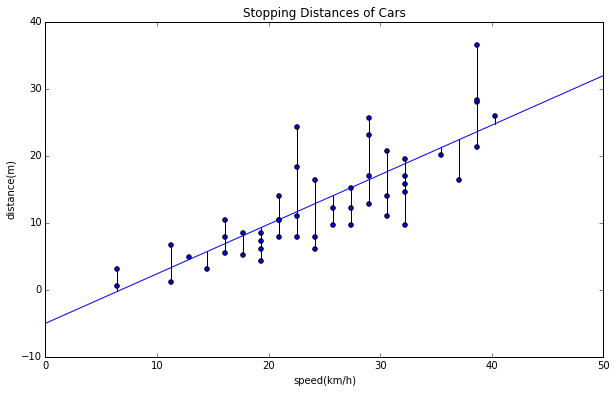
誤差とは各点から垂直な線を近似直線まで引いたものを表します。下記のグラフを見てください。
# line: y = 0.74 -5
x = [0, 50]
y = [-5, 32]
plt.plot(x,y)
# draw errors
for d in data:
plt.plot([d[1],d[1]],[d[2],d[1]*0.74-5],"k")
この黒い線で表されているのが誤差ですね。直感的にもこの誤差を全部足したものが一番少なくなるような直線が、このデータに一番フィットしている感じがしますね。
先ほど目視で当てはめた直線に対して、$\alpha$や$\beta$を変えた時のどうなるか見てみましょう。
まずは$\alpha$を変えてみた直線を見てみましょう。
# line: y = 0.54x -5
x = [0, 50]
y = [-5, 72]
plt.plot(x,y)
# draw errors
for d in data:
plt.plot([d[1],d[1]],[d[2],d[1]*1.54-5],"k")
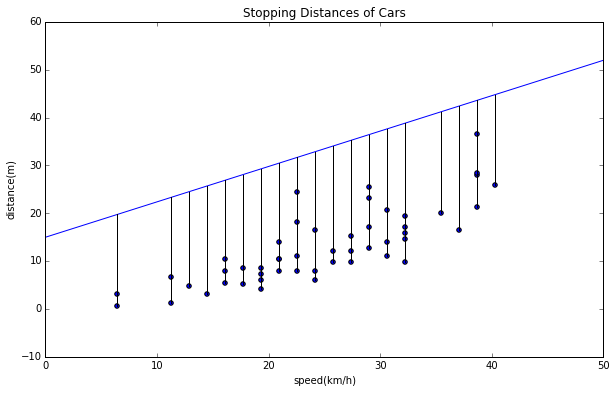
$\beta$を変えたものも見てみます。
# line: y = 0.74x +15
x = [0, 50]
y = [15, 52]
plt.plot(x,y)
# draw errors
for d in data:
plt.plot([d[1],d[1]],[d[2],d[1]*0.74+15],"k")
どうでしょう?最初に目視で良さそうな近似直線を引いたものと、あえて$\alpha$、$\beta$をずらしたものを比べるとこの誤差が少なそうに見えますよね。最小二乗法とはこの誤差を最小にする$\alpha$、$\beta$を求める方法なのです。
何を二乗する?###
これも、誤差を二乗するんです。なぜかというと、直線と各データの点を結ぶ直線の距離を求めたいのですが、そのままだと直線の上にあるデータは誤差がプラス、下にあるデータはマイナスとなってしまうので、二乗してプラスマイナスをとって全てプラスにしてしまうのです。
計算しよう###
では、何を二乗して、最小にするかがわかったところで具体的な計算を進めましょう。
まず用語の定義から。
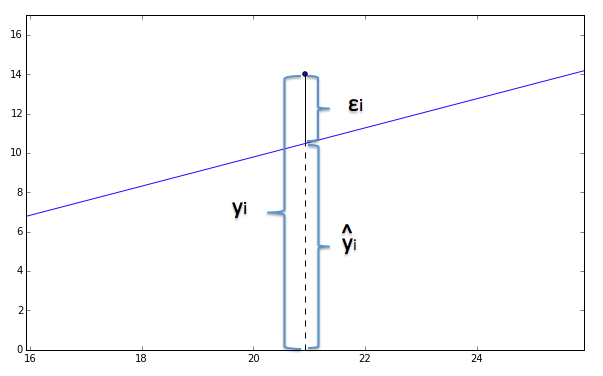
$i$番目のデータを$x_i, y_i$として、その近似値を$\hat{y}_i$と表します。
また、誤差を $\epsilon_i$とします。19番目のデータを拡大してみましょう。
i = 18
x_i = data[i,1]
y_i = data[i,2]
y_hat = x_i*0.74-5
ax.set_ylim(0,y_i+3)
ax.set_xlim(x_i-5,x_i+5)
plt.plot([x_i,x_i],[y_i,y_hat],"k")
plt.plot(x,y)
plt.scatter([x_i],[y_i])
さて、この誤差を二乗してデータ全て足し合わせると、
S = \sum_i^n\epsilon_i^2=\sum_i^n (y_i-\hat{y}_i )^2
と表現できます。
\hat{y}_i = \alpha x_i + \beta
なので、近似値データを代入すると下記になります。
S = \sum_i^n \epsilon_i^2 = \sum_i^n ( y_i-\alpha x_i - \beta )^2
この$S$をパラメータ$\alpha, \beta$で微分をして最小値を求めることで最適な近似直線が求められます。この$S$を$\alpha$の方程式で表すと、
S(\alpha) = \left( \sum_i^n x_i^2 \right) \alpha^2
+ 2\left( \sum_i^n (x_i\beta - x_i y_i ) \right) \alpha
+ n\beta^2 - 2\beta\sum_i^n y_i + \sum_i^n y_i^2
となる。この$S(\alpha)$ってどんな関数でしょう?$\alpha$の2次関数ですね。
$\alpha$の係数は二乗の和なので常に0かプラスの値ですので下に凸な2次関数となります。
ここで、形のイメージをつけるため、仮に$\beta=0$だったとしてグラフを書いてみましょう。
S(\alpha) = \left( \sum_i^n x_i^2 \right) \alpha^2
- 2\left( \sum_i^n x_i y_i \right) \alpha
+ \sum_i^n y_i^2 ... (if \beta = 0 )
と簡単になりますね。
データからこの係数を計算しましょう。
sum_x2 = np.sum([x ** 2 for x in data[:,1]]) # \sum x_i^2
sum_y2 = np.sum([x ** 2 for y in data[:,2]]) # \sum y_i^2
sum_xy = data[:,1].dot(data[:,2]) # \sum x_i y_i
print sum_x2
>>> 34288.2988
print sum_y2
>>> 11603.8684051
print sum_xy
>>> 18884.194896
よって、
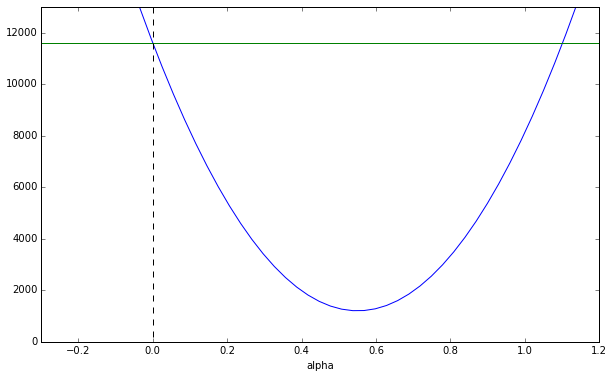
S(\alpha) ≒ 34288 \alpha^2 - 37768 \alpha + 11604
このグラフを描画すると、
x1 = np.linspace(-1,5,200)
x1_2 = np.array([x ** 2 for x in x1])
# 34288α2−37768α+ 11604
y1 = np.array(34288 * x1_2) - (37768 * x1) + 11604
plt.plot(x1,y1)
# Y = 11604の線
plt.plot([-1,5],[11604, 11604])
plt.plot([0,0],[13000, 0], "--k")
$\alpha$をずらしていくと、どこかで最小値が見つかることがわかります。
$\beta$も同様に、
S(\beta) = n\beta^2
+ 2 \left( \sum_i^n (x_i\alpha - y_i) \right) \beta
+ \alpha^2\sum_i^n x_i^2 - 2\alpha \sum_i^n x_iy_i + \sum_i^n y_i^2
仮に$\alpha=0$だったとしてグラフを書いてみましょう。
S(\beta) = n\beta^2
- 2 \left( \sum_i^n y_i \right) \beta + \sum_i^n y_i^2
... (if \alpha = 0 )
先ほど計算した値に$ \sum y_i$がなかったので計算すると(ついでに$\sum x_i$も)、
sum_x = np.sum(data[:,1])
print sum_x
>>> 1239.7
sum_y = np.sum(data[:,2])
print sum_y
>>> 655.0152
よって、$\beta$に関する2次方程式は
S(\beta) ≒ 50\beta^2 - 1310 \beta + 11604
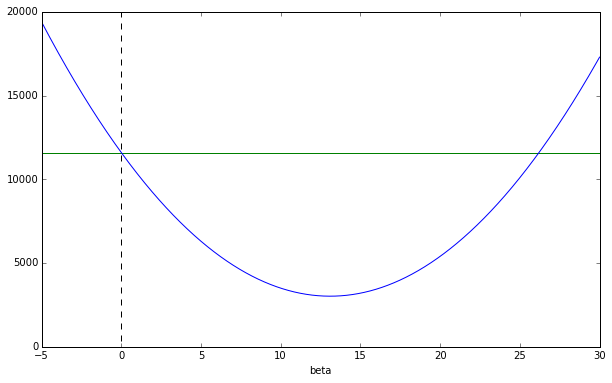
となり、グラフを描くと
x1 = np.arange(-100,100,0.01)
x1_2 = np.array([x ** 2 for x in x1])
n = len(data[:,2])
# nβ^2-1310β+11604
y1 = np.array(n * x1_2) - (1310 * x1) + 11604
fig = plt.figure(figsize=(10,6))
ax = fig.add_subplot(111)
ax.set_xlim(-5,30)
ax.set_ylim(0,20000)
ax.set_xlabel("beta")
plt.plot([-50,30],[11604,11604],"g")
plt.plot([0,0],[30000,0],"--k")
plt.plot(x1,y1)
と、やはり$\beta$をずらしていくと、ある$\beta$で最小値を取ることがわかります。
その2につづきます。