【3分でざっくり理解】「2標本t検定」をわかりやすく解説

[統計ソフト「JMP（ジャンプ）」によるt検定]


統計解析では、2つの異なるグループの平均値を比較したい場面がよくあります。たとえば、「新薬を服用したグループと従来の薬を服用したグループで血糖値の平均に差があるか」といった状況です。

このような場合に用いられる基本的な手法が2標本t検定です。本記事では、この検定についてわかりやすく解説します。

2標本t検定とは

2標本t検定は、2つの独立したグループの平均値に統計的な有意差があるかを調べる検定です。

2標本t検定が使われる場面

冒頭で紹介した例以外では、たとえば、以下のようなデータに適用できます。

• 2つの学生グループ（英語を母国語とする生徒とそうでない生徒）の英語試験の平均点
• 男性と女性の体重の平均値
• 都市部と地方部でのサラリーマンの平均収入

2標本t検定の前提条件

2標本t検定を正しく適用し、妥当な検定を行うためには、次の要件を満たす必要があります。

1. データが正規分布している
   各グループのデータが正規分布に従っていることが前提です。
2. データ値が独立している
   2つのグループのデータが互いに関連していないことが条件です。たとえば、同じ個人を2回測定している場合は、この検定は適しません（この場合は対応のあるt検定を使います）。
3. 分散が等しい（または等しくない場合は対応する手法を使用）
   両グループのデータの分散が等しくなっている必要があります。分散が等しくない場合にはウェルチのt検定を用います。
4. データ値は連続変数である
5. 各グループのデータは母集団から無作為に抽出されている

2標本t検定の実施手順

1)帰無仮説と対立仮説の設定
統計的仮説検定では、検証したい内容と反対の内容を「帰無仮説（H₀）」として設定し、この帰無仮説を棄却することを目指します。

・帰無仮説（H₀）：2つのグループの平均値に差はない（μ₁ ＝ μ₂）
・対立仮説（H₁）：2つのグループの平均値に差がある（μ₁ ≠ μ₂）

2)有意水準の設定
帰無仮説を棄却する際の判断基準として、データの希少性を判断する基準である有意水準を設定します。有意水準は、0.05（5％）を用いるのが一般的です。

3)検定統計量の算出
比較する標本データ間に有意な差があるか否かを示す検定統計量を計算します。検定統計量は標本の平均値の差、プールした標準偏差、標本サイズを用いて算出します。

・検定統計量の計算
検定統計量は以下の式で計算されます：

\begin{flalign}
  &
t=\displaylines{

\frac{\bar{X_1}-\bar{X_2}}{\sqrt{S^2_p (\frac{1}{n_1}+\frac{1}{n_2})}
}}
&
\end{flalign}

ここで、

\begin{flalign}
  &
・\bar{X_1},\bar{X_2}：それぞれのグループの平均値
&
\end{flalign}

\begin{flalign}
  &
・n_1,n_2：各グループのサンプルサイズ
&
\end{flalign}

\begin{flalign}
  &
・S^2_p：プールした分散（以下で計算）
&
\end{flalign}

\begin{flalign}
  &
S^2_p=\displaylines{

\frac{(n_1-1)S^2_1+(n_2-1)S^2_2}{n_1+n_2-2
}}
&
\end{flalign}

\begin{flalign}
  &
・S^2_1,S^2_2は各グループの分散です。
&
\end{flalign}

分散が等しくない場合（ウェルチのt検定）では、別の式が使われます。

4) t値の決定
検定統計量を算出した後は、男性と女性の平均が等しいという帰無仮説の下で、t分布から理論値を見つけます。この値はt分布表に有意水準（0.05）と自由度を当てはめて得られます。

5)結論の導出
算出した検定統計量と、4)のt値を比較します。この検定統計量よりt値が小さければ帰無仮説が棄却されます 。

実例で考える

ケース：頻繁にジムに通う男女の平均体脂肪率は等しいのか？
以下の標本データは、1年間、週に5回ジムでトレーニングに励む男女グループの体脂肪率を測定したものです。このデータをもとに、ジムに通う男性と女性の母集団の体脂肪率の平均値に差があるのかを確認します。

手順
1. 前提条件の確認
1) データが正規分布している
今回、データは正規分布していると仮定します。

2) データ値が独立している
ある人の体脂肪率は別の人の体脂肪率とは無関係なので、データは独立しています。

3) 分散が等しい（または等しくない場合は対応する手法を使用）
両グループのデータの分散が等しいと仮定して進めます。

4) データ値は連続変数である
今回の測定値は体脂肪率であり、体脂肪率は連続変数です。

5) 各グループのデータは母集団から無作為に抽出されている
今回測定した男女は、ジム会員の母集団から無作為に選ばれたと仮定します。

2. 仮説設定
・帰無仮説：μ₁ ＝ μ₂（男性と女性の体脂肪率の平均値に差はない）
・対立仮説：μ₁ ≠ μ₂（男性と女性の体脂肪率の平均値に差がある）

3. 検定統計量の計算
まず、男女のグループごとの、

\begin{flalign}
  &
平均値(\bar{X_1})、標準偏差(S)、および標本サイズ(n)は以下になります。
&
\end{flalign}

グループ	標本サイズ	平均値	標準偏差
女性	10	22.29	5.32
男性	12	16.11	5.65

この表からは、男女の体脂肪率の平均値に差があるように見えますが、これは男女の母集団についても言えるのか確認しましょう。

では、前述の検定統計量 の計算式を用いて算出してみます。

\begin{flalign}
  &
t=\displaylines{

\frac{\bar{X_1}-\bar{X_2}}{\sqrt{S^2_p (\frac{1}{n_1}+\frac{1}{n_2})}
}}
&
\end{flalign}

\begin{flalign}
  &
・\bar{X_1},\bar{X_2}：それぞれのグループの平均値
&
\end{flalign}

\begin{flalign}
  &
・n_1,n_2：各グループのサンプルサイズ
&
\end{flalign}

\begin{flalign}
  &
・S^2_p：プールした分散（以下で計算）
&
\end{flalign}

\begin{flalign}
  &
S^2_p=\displaylines{

\frac{(n_1-1)S^2_1+(n_2-1)S^2_2}{n_1+n_2-2
}}
&
\end{flalign}

\begin{flalign}
  &
・S^2_1,S^2_2は各グループの分散です。
&
\end{flalign}

ここで、

\begin{flalign}
  &
・\bar{X_1}-\bar{X_2}：22.29−16.11=6.18
&
\end{flalign}

\begin{flalign}
  &
S^2_p=\displaylines{

\frac{(n_1-1)S^2_1+(n_2-1)S^2_2}{n_1+n_2-2
}}=\displaylines{

\frac{((10-1)5.32^2)+((12-1)5.65^2)}{(10+12-2)
}}=\displaylines{

\frac{(9 \times 28.30)+(11 \times 31.92)}{20
}}=\displaylines{

\frac{254.7+351.15}{20
}}=\displaylines{

\frac{605.85}{20
}}=30.29
&
\end{flalign}

[右にスクロールして数式の続きを確認できます]

\begin{flalign}
  &
\sqrt{S^2_p (\frac{1}{n_1}+\frac{1}{n_2})}=\sqrt{30.29(\frac{1}{10}+\frac{1}{12})}=2.36

&
\end{flalign}

したがって、

\begin{flalign}
  &
t=\displaylines{

\frac{\bar{X_1}-\bar{X_2}}{\sqrt{S^2_p (\frac{1}{n_1}+\frac{1}{n_2})}
}}=\displaylines{

\frac{6.18}{2.36
}}=2.62
&
\end{flalign}

となります。

4. t値の決定
次にt値をt分布表で見つけます。今回、有意水準は0.05（5％）に設定するものとし、自由度は20（10+12-2）です。この場合のt値（棄却限界値）は2.086です。

5. 結果解釈
算出した検定統計量tとt値を比較します。

検定統計量t（2.62）>t値(2.086)

であるため、「男性と女性の体脂肪率の平均値に差はない」という帰無仮説が棄却され、ジムの母集団の体脂肪率の平均は、男性と女性で異なると結論付けられます。

JMPで2標本のt検定

ここまで、手計算で2標本t検定の実施法を説明しました。ですが、実務では計算に時間と手間がかかるので、統計ソフトを使うのが一般的です。そこで、最後に簡単に統計ソフト「JMP（ジャンプ）」による2標本t検定の実施法をご紹介します。

1.縦に積んだデータをあらかじめ用意して、JMPでそのデータを開きます。

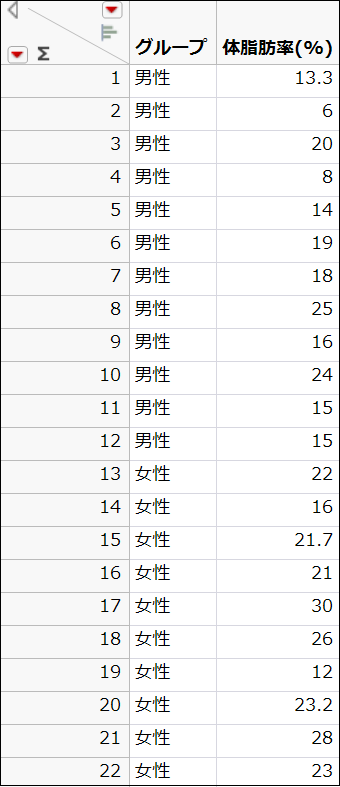
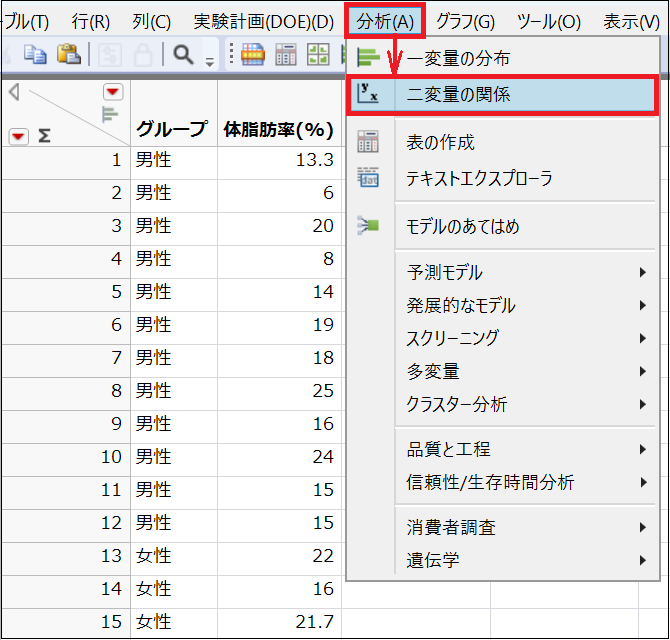
2.JMPでは一元配置分析のなかにt検定が含まれています。そこで、画面上の「分析」>「二変量の関係」と進み、「X, 説明変数」に「グループ」、「Y, 目的変数」に「体脂肪率（%）」を入れて「OK」を押します。

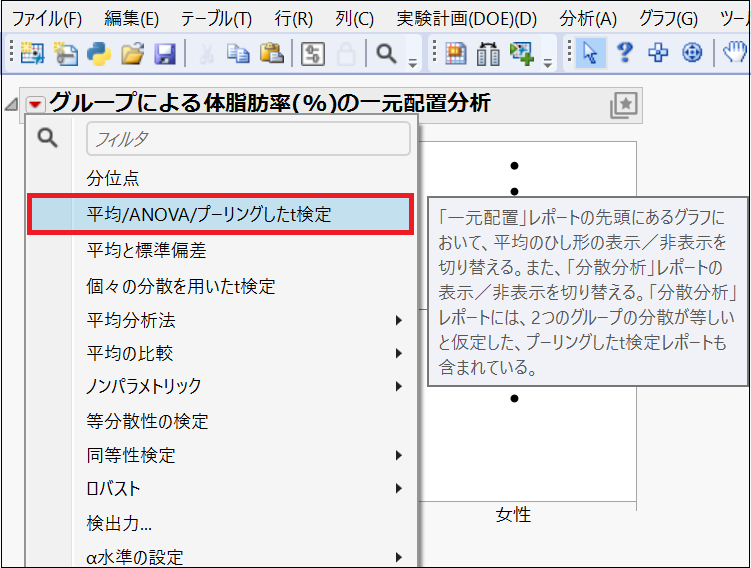
すると、下のように一元配置分析のレポートが表示されるので、左上の赤三角から「平均/ANOVA/プーリングしたt検定」を選びます。

［元は「女性」「男性」の順ですが、ここでは入れ替えて表示しています。]

3.一元配置分析のレポートの下にプーリングしたt検定のレポートが表示されました。

データのファイルを開いてから、このレポートの表示まで数分（慣れると1分以下）しかかからず、手計算よりもはるかに手軽で時間の短縮になります。

また、1つのウィンドウに表示されるレポート内に、男女のデータのばらつきや平均値、検定統計量、上側＆下側信頼限界、p値など必要な情報がわかりやすくまとまっています。

そのため、手計算から解放されて余った時間は、データから何が読み取れるのか分析にあてることができるのです。

いかがでしたか？今回の記事で2標本t検定のイメージをつかんでいただけたなら嬉しいです。統計ソフトを使った分析に関心のある方は下のトライアル版も試してみてください！

統計ソフトを今まで使ったことがなくてもご心配なく。
統計ソフト「JMP（ジャンプ）」には、30日間すべての機能を無料で利用できるトライアル版があります。よければ試してみてください。

30日間全機能無料のトライアル版はこちら
https://www.jmp.com/ja_jp/download-jmp-free-trial.html?utm_campaign=bl&utm_source=JMPblog&utm_medium=social

t検定について、さらに詳しく知りたい方は以下のWebページもおすすめです。

【3分でざっくり理解】t検定とは？具体例で初心者にもわかりやすく
https://qiita.com/JMP_Japan/items/6538ae8a4c8261648159


【3分でざっくり理解】 「1標本のt検定」をわかりやすく解説
https://qiita.com/JMP_Japan/items/4a924c361206e2b862cd


【3分でざっくり理解】「対応のあるt検定」をわかりやすく解説
https://qiita.com/JMP_Japan/items/7c7d8787a8300b7827ca


Statistics Knowledge Portal (t検定)
https://www.jmp.com/ja_jp/statistics-knowledge-portal/t-test.html?utm_campaign=bl&utm_source=JMPblog&utm_medium=social