[統計ソフト「JMP（ジャンプ）」によるt検定]
この記事ではt検定を初心者の方にもわかりやすく簡潔に説明します。t検定は、さまざまなビジネスの現場でも利用されるので、しっかり理解して使えるようになりたいですね。それでは始めましょう！
※今回の内容はYouTube動画でもご紹介しています。
t検定とは
t検定とは、2つの標本の平均値を比較する際に、その差が偶然なのか、それとも本当に差があるのか（統計的に有意な差と言えるか）を統計学的に判定する手法です。
t検定が使われる場面
t検定は、たとえば以下のような場面で利用されることがあります。
- 製造業の生産現場での品質データ管理
- 製薬業における治験データをもとにした新薬の効能判定
- マーケティングの広告キャンペーンの有効性検証
t検定の前提条件
t検定を使用するには、次の3つの条件を満たすことが必要です。
a. 母集団の分布が正規分布に従っている
b. 等分散性がある（比較を行う母集団間の分散が等しい）
c. 標本データが母集団から無作為にサンプリングされている
t検定の実施手順
t検定を実施する流れは次のようになります。
1. 帰無仮説と対立仮説の設定
統計的仮説検定では、検証したい内容と反対の内容を「帰無仮説（H0）」として設定し、この帰無仮説を棄却することを目指します。
・帰無仮説（H0）：
検証したい効果や差異がないと仮定する（例: 2つの標本データの平均は等しく、差があっても誤差や偶然である）。
・対立仮説（H1）：
検証したい効果や差異があることを示す（例: 2つの標本データの平均は異なる）。
2. 有意水準の設定
帰無仮説を棄却する際の判断基準として、データの希少性を判断する基準である有意水準を設定します。有意水準は、0.05（5％）を用いるのが一般的です。
3. t値の算出
比較する標本データ間に有意な差があるか否かを示すt値を計算します。t値はデータから標本の平均、標準偏差、サンプルサイズを用いて算出します。
数式を使って手計算でt値を求めると時間や労力がかかってしまうため、業務で時間がないときは、自動で算出してくれる統計ソフトを使うと便利です。
4. p値の決定
t値を算出した後は、得られたデータの希少性を表す確率値であるp値を求めます。p値は「t分布表」にt値と自由度を当てはめて得られますが、そのやり方では、やはり手間がかかってしまうため、統計ソフトで自動算出することが多いです。
5. 結論の導出
算出したp値と、2で設定した有意水準を比較します。有意水準よりp値が小さければ、その標本データは極めて稀で珍しいと言えます。
その場合、帰無仮説は棄却され、対立仮説が採択されます。これによって、2つの平均値は統計的に有意な差があると解釈できます。
手間をかけずにt検定を実施
ここまでt検定実施の際の流れをざっくりと説明しました。より詳しく知りたい方は、数式を用いて手計算で実施する解説記事を、web上に幾つか見つけることができるはずです。
ですが、業務でそこまで手間をかけられないという方のために、統計ソフトを使った実施法もおまけで説明します。
統計ソフトを今まで使ったことがなくてもご心配なく。
統計ソフト「JMP（ジャンプ）」には、30日間すべての機能を無料で利用できるトライアル版があります。よければ試してみてください。
30日間全機能無料のトライアル版はこちら
https://www.jmp.com/ja_jp/download-jmp-free-trial.html?utm_campaign=bl&utm_source=JMPblog&utm_medium=social
では、対応のないt検定について例題を見てみましょう。
【例題】
糖尿病患者に対して、治療薬Aと対照薬のいずれかを投与し、投与3か月後のヘモグロビンA1c（以下、HbA1c）を測定したデータ（%）が得られた。
| 治療薬A群（12例） | 対照薬群（14例） |
|---|---|
| 6.7 | 9.8 |
| 6.8 | 9.6 |
| 9.0 | 8.3 |
| 8.8 | 8.9 |
| 6.5 | 8.1 |
| 7.7 | 7.9 |
| 8.1 | 8.7 |
| 7.5 | 8.3 |
| 6.5 | 6.7 |
| 9.5 | 8.8 |
| 6.6 | 6.9 |
| 5.9 | 10.0 |
| 8.0 | |
| 7.8 |
治療薬A群と対照薬群のHbA1cについて、（Studentの）t検定を実行し、平均値の差を比較する。
注) HbA1cは、右側に裾を引く非対称分布になると言われていますが、ここでは正規性を仮定し、話を進めます。
1)まず、帰無仮説を設定します。今回は、「治療薬A群と対照薬群のHbA1c測定データ(%)の平均が等しい」になります。
2)次に、データを準備します。JMPで対応のないt検定を実行するには、下のように積み上げ形式のデータを用意する必要があります。例題は合計26例を対象にしているので、データの行数は26行になります。
[積み上げ形式のデータの一部]
3)今回、投与薬の違いが3か月後のHbA1cに差をもたらすかを確認しますが、JMPでは「投与薬」と「3か月後のHbA1c」の2つの変数間に関連があるかどうかをみると考えます。
そこで、画面上の［分析］>［二変量の関係］と進み、［Y,目的変数］に「3か月後HbA1c（%）」、［X,説明変数］に「投与薬」を入れます。
Yに連続尺度、Xに名義尺度（または順序尺度）を指定した場合は、Xの群ごとに連続値Yを比較するためのレポート（一元配置分析）が表示されます。
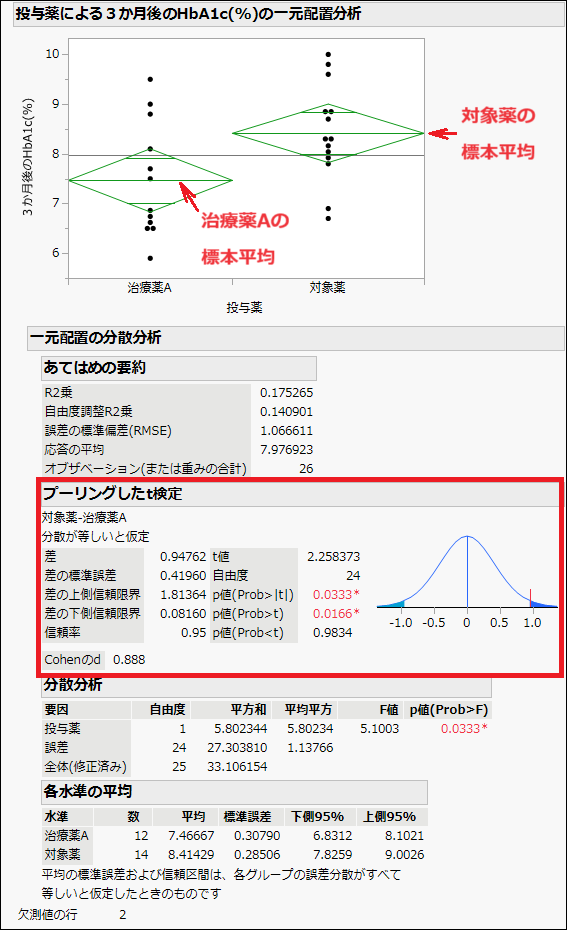
さらに、レポート左上の赤い三角ボタン（▼）から、［平均/ANOVA/プーリングしたt検定］を選択すると、ダイヤモンドに似た緑のひし形がグラフに追加されました。
このひし形は、JMP独自のもので、グループの統計量を可視的に表示しており、たとえば、中央の1番長い横線はそのグループの標本平均を表しています。
これを見るだけで2つのグループ間の標本平均にそれなりの差があることがひと目で見て取れますね。
JMPでは、単純にp値だけで解釈するのではなく、最初にグラフからグループのデータの違いを可視的に考察できるので便利です。
そして、そのグラフの下にt検定のレポートが表示されます。
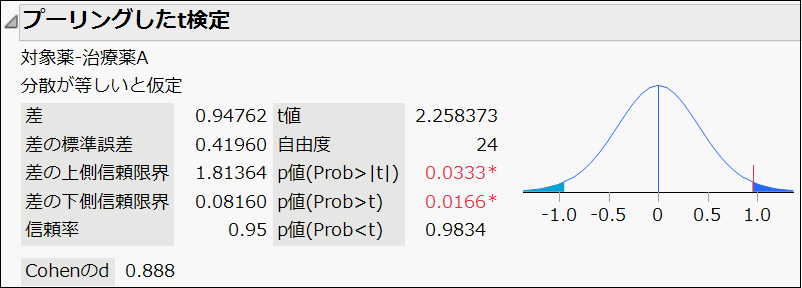
4)統計ソフトの場合は手計算をする必要がないので、t値、自由度、p値を一瞬で求めることができます。また、このt検定のレポートには、これらの値だけではなく対照薬–治療薬A に対する平均の差や、差の標準誤差も表示されています。
そして、このレポートによると、両側検定のp値は0.0333とあり、今回設定した有意水準(0.05)より小さいため、帰無仮説を棄却できます。
これによって、測定データの平均値に統計的に有意な差があることが分かりました。
いかがでしたか？t検定とはどのような統計手法なのか、今回の記事でイメージをつかんでいただけたなら嬉しいです。
t検定について、さらに詳しく知りたい方は以下のWebページもおすすめです。
【3分でざっくり理解】 1標本のt検定を分かりやすく解説
https://qiita.com/JMP_Japan/items/4a924c361206e2b862cd
【3分でざっくり理解】「対応のあるt検定」をわかりやすく解説
https://qiita.com/JMP_Japan/items/7c7d8787a8300b7827ca
Statistics Knowledge Portal (t検定)
https://www.jmp.com/ja_jp/statistics-knowledge-portal/t-test.html?utm_campaign=bl&utm_source=JMPblog&utm_medium=social