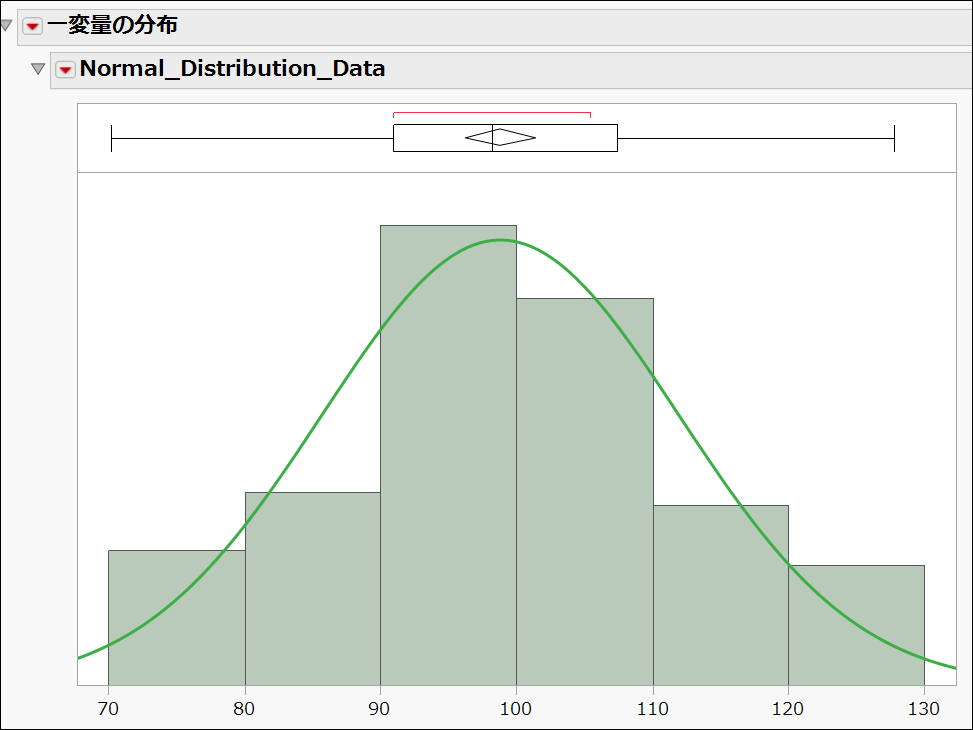
[統計ソフト「JMP(ジャンプ)」で描いた正規分布のグラフ]
※今回の内容はYouTube動画でもご紹介しています。
正規分布とは?
「正規分布」とは、平均値付近にデータが最も多く集まり、そこから離れるにつれてデータの数が減っていくという特徴をもつ、連続的な確率分布です。
正規分布の特徴
この正規分布には以下の特徴があります。
1. 平均値、中央値、最頻値が一致する
2. 平均値を中心にして対称である
3. 平均と標準偏差の2つで正規分布の図を描くことができる
4. 「釣り鐘」の形をしている
その形状がなだらかな「釣り鐘」に似ていることから、正規分布は「ベルカーブ(Bell Curve)」の名でも知られています。
なぜ正規分布は重要なのか?
多くの統計手法は、「データが正規分布に従う」という前提のもとに成り立っています。そして、この前提が成り立つことで、正確な推論や効率的なデータ分析が可能になるのです。
たとえば、信頼区間の算出や p 値の計算など、正規分布を基盤とした統計手法は数多く存在しますし、線形回帰などの機械学習アルゴリズムは、データが正規分布に従うことが前提になっています。
また、正規分布は、実務の現場でも幅広く活用されています。
たとえば製造業では、製品の寸法や性能のばらつきを正規分布として可視化することで、工程の安定性確保や製品の品質管理に役立っています。
正規性を確認する方法は?
正規分布かどうかを確認する方法は、大きく分けて2つあります。
ひとつはグラフで目視する方法、もうひとつは統計的に検定する方法です。
1. グラフで視覚的に確認する方法
グラフで正規性を確認する場合は、ヒストグラムや箱ひげ図、正規分位点プロット(QQプロット)などを利用します。
1)ヒストグラムによる方法

ヒストグラムを使ってデータに正規性があるかを視覚的に確認するときは、グラフに次の特徴が見られるかどうかをチェックします。
・極端な値(外れ値)がないか
・グラフがほぼ対称になっているか
・全体がなだらかな「ベル型」の形をしているか
上のグラフでは、極端な値があり、対称でもなく、ベル型の形にもなっていないため、正規性は認められません。
2) 箱ひげ図による方法
データの正規性は箱ひげ図でも確認できます。
箱ひげ図によって正規性の確認をする場合、グラフに次の特徴が見られるかどうかをチェックしてみましょう。
・極端な値(外れ値)がないか
・グラフが対称的か否か
・平均値と中央値がほぼ等しいか

たとえば、こちらの箱ひげ図では、外れ値はなく、グラフは対称的で、平均値と中央値がほぼ等しいため、データがほぼ正規分布に従っていると言えそうです。

他方で、上の箱ひげ図では、外れ値が5つあり、グラフは非対称的で、平均値と中央値が等しくないため、データが正規分布に従っていないと言えそうです。
3) 正規分位点プロット(QQプロット)による方法
正規分位点プロット(QQプロット)は、正規分布をベルカーブではなく直線として可視化したものです。
もしデータが正規分布に従っていれば、データ点は下のグラフのようにほぼ一直線上に並びます。

一方で、正規分布から外れている場合は、下のグラフのようにデータ点は直線から大きくずれます。

このずれ方のパターンを見ることで、データの特徴や正規分布していない原因を推測することができます。
2. 統計的に検定する方法
データが正規分布に従うかを調べる代表的な方法が正規性の検定です。よく使われる検定には以下の3つがあります。
• シャピロ–ウィルク検定
o 正規性の検定において、一般的かつ広く使われる手法
o サンプルサイズが小さい場合に最適
• コルモゴロフ–スミルノフ検定(K-S検定)
o データの分布と正規分布のような一般的な確率分布の差を調べる検定(1標本の場合)
o 中~大規模データに対応
• アンダーソン–ダーリング検定
o 分布の両端(尾部)の形状に敏感
o 極端な値の影響も反映しやすい
これらの検定では、帰無仮説と対立仮説を以下のように設定し、p値を確認します。
◆ 帰無仮説 (H0) :データの分布は正規分布に従っている
◆ 対立仮説 (H1) :データの分布は正規分布に従っていない
このように帰無仮説と対立仮説を設定すると、少しわかりづらいかもしれませんが、p値については次のように理解されます。
-
p値 ≥ 0.05 →帰無仮説が棄却されない→「データ分布が正規分布に従っていない」とする根拠がない→データ分布は正規分布に従っているとみなされる
-
p値 < 0.05 →帰無仮説が棄却されて、対立仮説が採用される→「データ分布が正規分布に従っていない」とみなされる
統計ソフトJMPで正規性を調べる
ところでこの正規性の検定は、統計ソフトを使うと手軽で直感的に行えます。ここでは、JMP(ジャンプ)を使った実施方法をご紹介します。
JMPには30日間無料で全機能を試せるトライアル版があります(自動課金なし)。
https://www.jmp.com/ja_jp/download-jmp-free-trial.html?utm_campaign=bl&utm_source=blog&utm_medium=JMPblog
では、さっそく操作を始めましょう。JMPで用意されているサンプルデータの中から、今回は「Car Physical Data」を使って正規性を確認してみます。
サンプルデータ:Car Physical Data
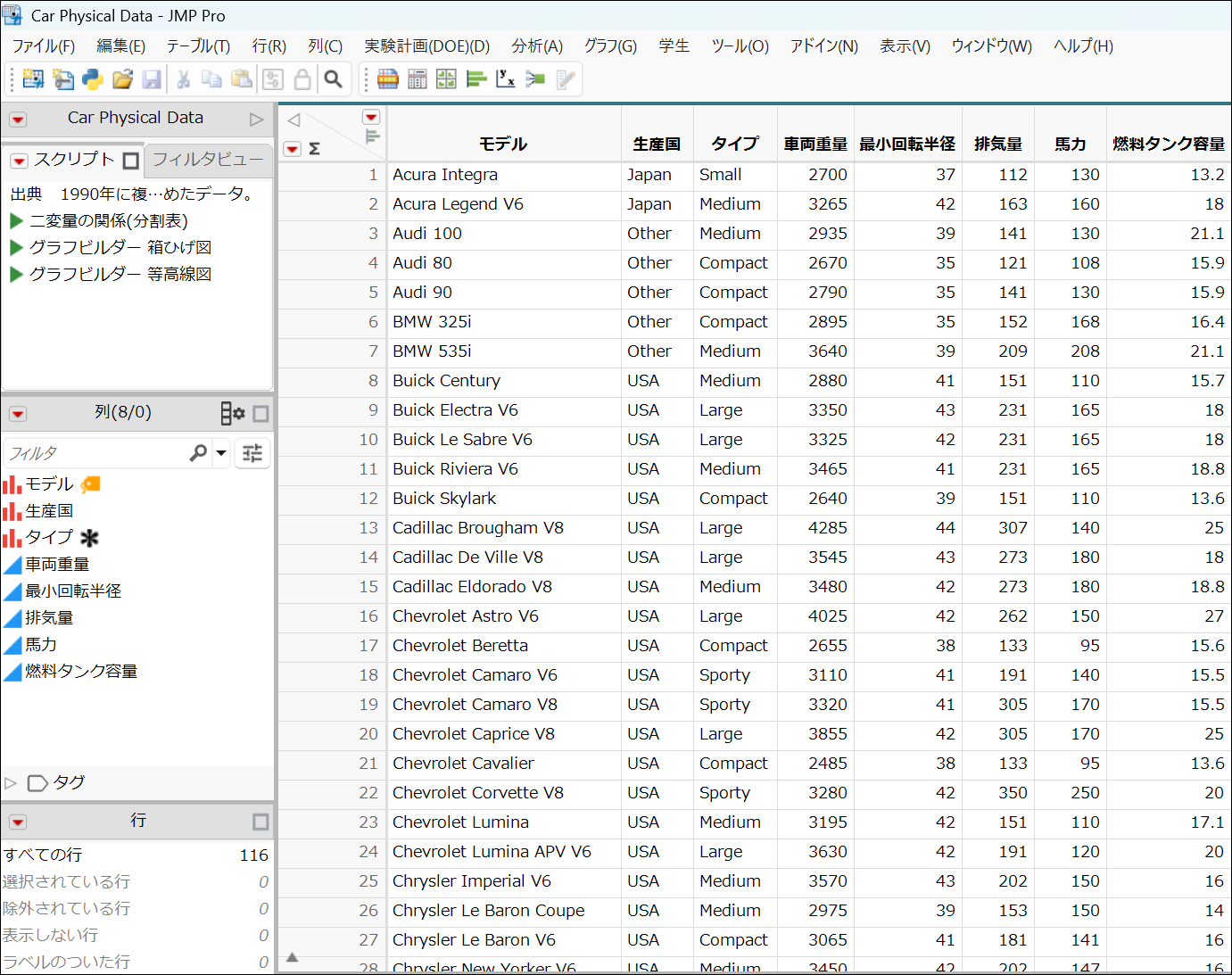
このデータセットには、116種類の車についての情報が含まれています。生産国や馬力などさまざまな項目がありますが、今回は 「車両重量」 と 「排気量」 の2つのデータを例に、正規性を確認してみましょう。
1. JMPのグラフで視覚的に確認する方法
1)ヒストグラムと箱ひげ図
「分析」から「一変量の分布」と進み、「車両重量」「排気量」を「Y, 列」に入れて「OK」を押すと、ヒストグラムや箱ひげ図とともに下のレポートが表示されます。
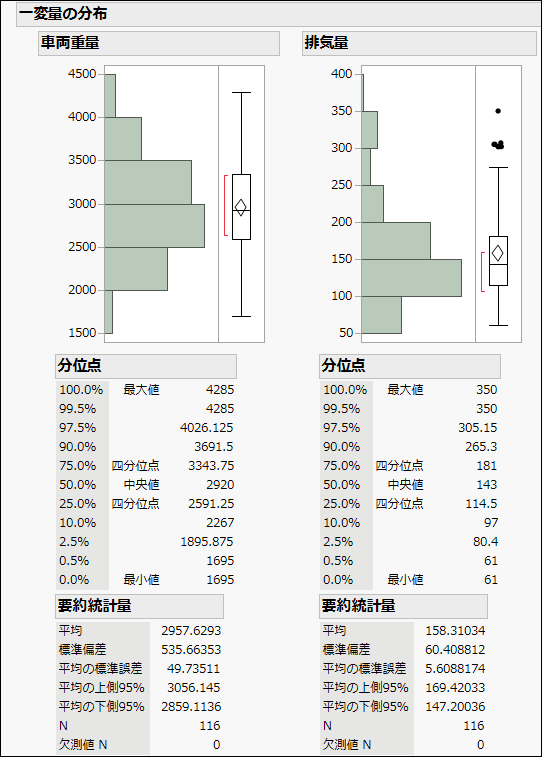
正規性を視覚的に確認してみましょう。左側の「車両重量」データのヒストグラムは、おおむね対称的な釣り鐘型をしています。また、箱ひげ図では平均値と中央値がほぼ一致し、外れ値もほとんどありません。

※JMPの箱ひげ図では、上の図のように平均値も一緒に表示されます。
一方、右側の「排気量」データのヒストグラムは釣り鐘型とは言えず、箱ひげ図は平均値と中央値に差があり、外れ値も複数確認できます。
これらのことから、「車両重量」 データは正規性があると考えられ、「排気量」 データは正規性がない可能性が高いことがわかります。
2) 正規分位点プロット(QQプロット)
次に、同じレポートウィンドウに正規分位点プロット(QQプロット)を表示してみましょう。操作は簡単です。
キーボードのCtrlキーを押しながら、「車両重量」の横にある赤い三角ボタンをクリックし、メニューから「正規分位点プロット」を選択します。
JMPではこのようにCtrlキーを押しながらコマンドを選択すると、ウィンドウ内のすべての同種レポートに同じコマンドが適用されます。
それでは、レポートを見てみましょう。
「車両重量」だけでなく、「排気量」にも、先ほどのヒストグラムや箱ひげ図の横に、正規分位点プロット(QQプロット)が追加されました。
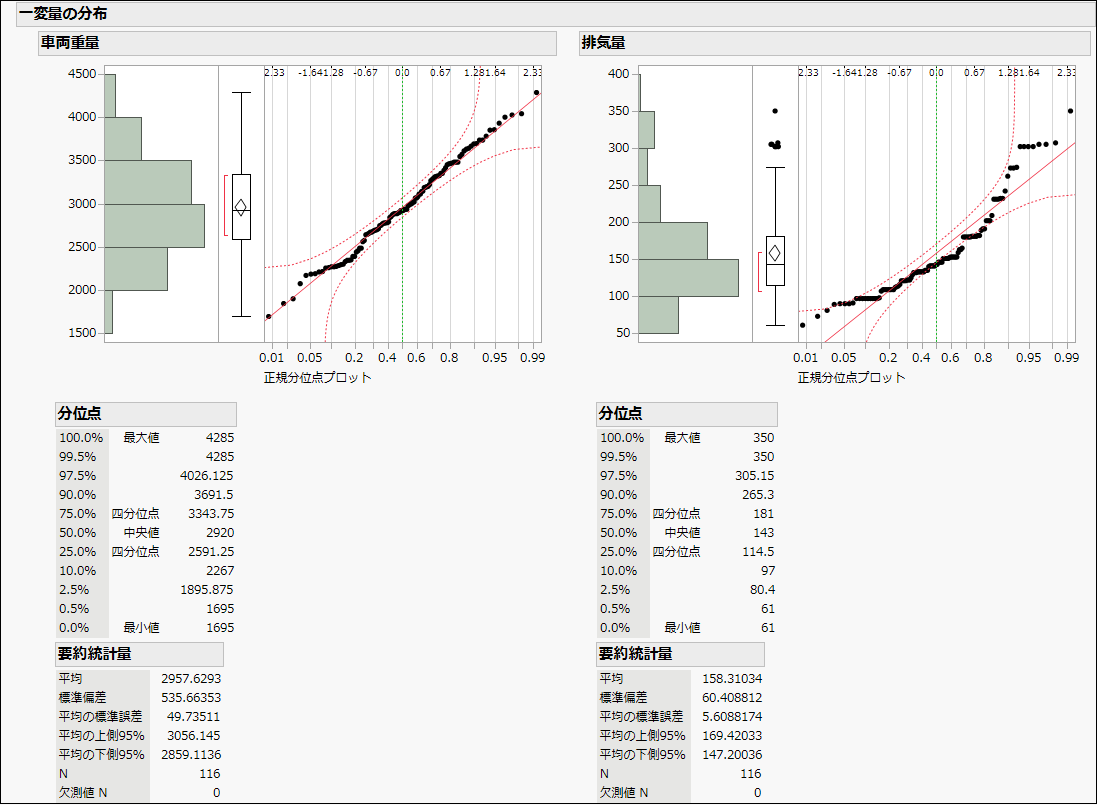
正規分位点プロット(QQプロット)では、データが正規分布に従う場合、データ点が赤い実線の近くに分布します。また、弓状の赤い点線は信頼区間を示しており、正規分布に従うデータでは、すべての点がこの範囲内に収まります。
今回の結果を見ると、左側の「車両重量」ではデータ点がほぼ一直線上に並んでおり、正規分布に近いことがわかります。一方、右側の「排気量」では、データ点が直線から大きく外れており、正規性がないことが示唆されます。
これらのグラフを確認することで、データの分布の特徴を視覚的に把握できました。
具体的には、「車両重量」データはヒストグラムで釣り鐘型に近く、箱ひげ図では平均値と中央値がほぼ一致し、さらに正規分位点プロット(QQプロット)で直線性を示していることから、正規分布に従っている可能性が高いと考えられます。
次に、同じ操作を使ってヒストグラムに正規分布を当てはめてみましょう。
キーボードのCtrlキーを押しながら、「車両重量」 の横にある赤い三角ボタンをクリックし、「連続分布のあてはめ」→「正規のあてはめ」 を選択します。
すると、ヒストグラムにベルカーブが重ねて表示されました。
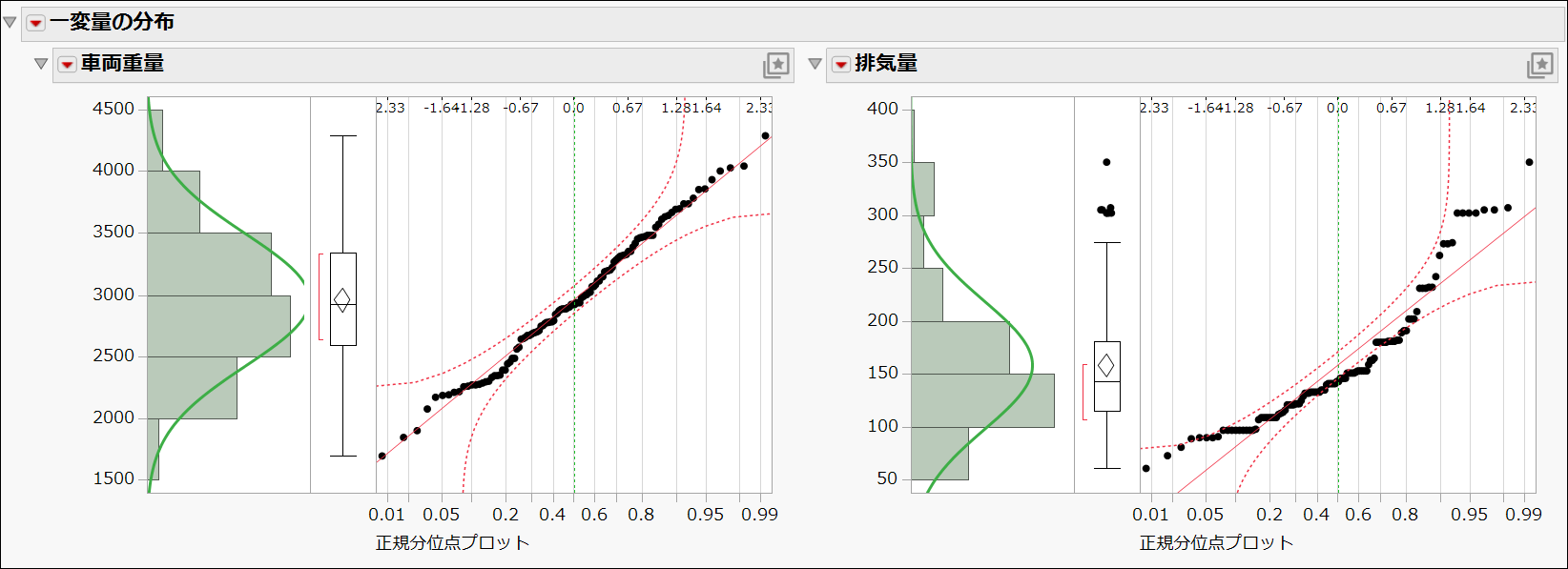
1つのウィンドウに ヒストグラム、箱ひげ図、QQプロット、正規分布曲線 をまとめて表示できるのは、JMPの可視化機能の大きな特徴です。
これにより、データの分布や正規性を直感的に理解しやすくなります。
2.JMPで統計的に検定する方法
さらにJMPで統計的検定を実施してみましょう。
レポートの最下部にある「正規分布のあてはめ」の横の赤い三角ボタンを、キーボードのCtrlキーを押しながらクリックし、プルダウンの中から「適合度」を選択します。
すると、統計的な適合度の検定結果が表示されました。
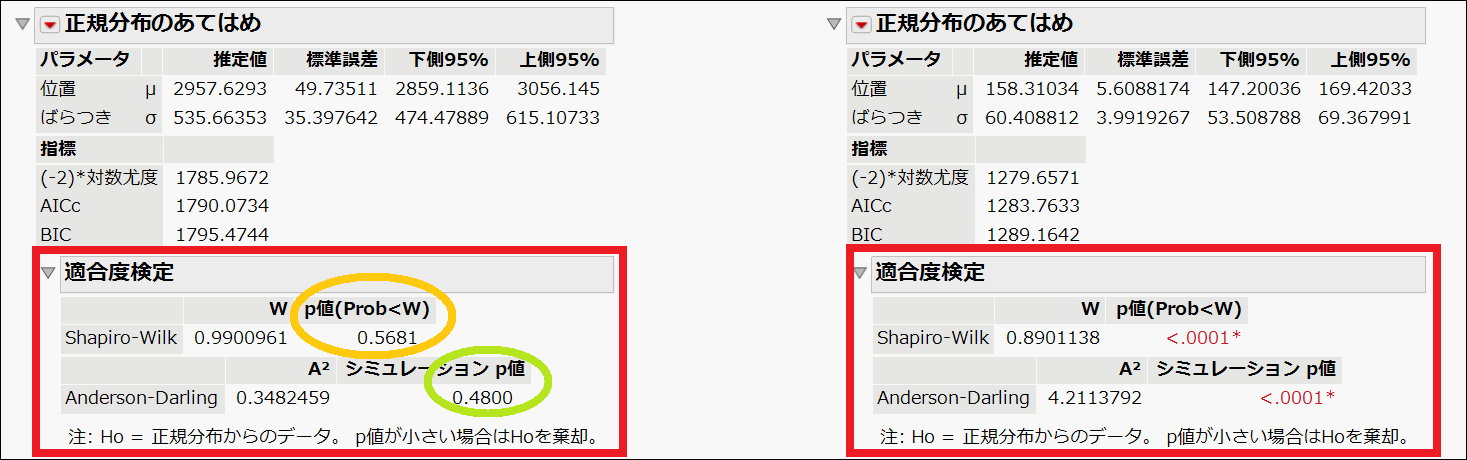
ここでシャピロ–ウィルク検定(Shapiro-Wilk)とアンダーソン–ダーリング検定(Anderson-Darling)の結果を確認してみましょう。
左の「車両重量」データでは、両検定とも p値 ≥ 0.05 です。
そのため、帰無仮説を棄却できず、正規分布に従わない根拠はないと判断できます。
つまり、このデータ分布は正規分布に従っているとみなせます。
一方、「排気量」データでは、両検定とも p値 < 0.05 です。
この場合、帰無仮説が棄却され、対立仮説が採択されます。
したがって、データ分布は正規分布に従っていないとみなされます。
いかがでしたか?
手持ちのデータが正規分布に従っているか確認したいとき、JMPなら1つのウィンドウで視覚的にも統計的にも確認できます。
この記事を通じて、正規分布の考え方やJMPを使った確認方法のイメージをつかんでいただけたら嬉しいです。ぜひご自身のデータでも試してみてください!
さらに詳しく知りたい方は、以下のページもぜひご覧ください。
Statistics Knowledge Portal:正規分布
https://www.jmp.com/ja/statistics-knowledge-portal/measures-of-central-tendency-and-variability/normal-distribution
また、JMPを実際に触ってみたい方は、以下のトライアル版もおすすめです。
最新バージョンJMP 19 が使える!30日間全機能無料 JMPトライアル版(自動課金なし)
https://www.jmp.com/ja_jp/download-jmp-free-trial.html?utm_campaign=bl&utm_source=blog&utm_medium=JMPblog