第K最短路のプログラム作成
Q&A
Closed
解決したいこと
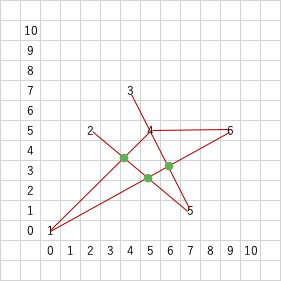
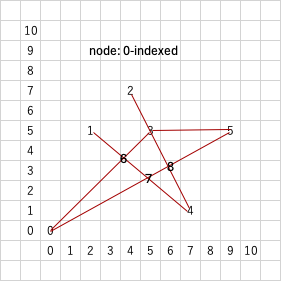
与えられた始点と終点に対して、1<=k<=5番目までの短い経路の距離を求めたい
発生している問題・エラー
k=1(最短経路)の距離を求めるプログラムは完成しているが、k>=2以降を求める方法が分からない
該当するソースコード
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <string.h>
#define MAXN 1100 // 最大ノード数(地点+交差点)
#define MAXM 500 // 最大セグメント数(線分の数)
#define MAXQ 100 // 最大クエリ数
#define INF 1e18 // 無限大の代用
#define EPS 1e-8 // 誤差の許容範囲
// 座標を表す構造体
typedef struct {
double x, y;
} Point;
// 線分を表す構造体(2点のインデックス)
typedef struct {
int a, b;
} Segment;
// グラフのエッジを表す構造体(隣接リスト形式)
typedef struct Edge {
int to; // 接続先ノード
double cost; // コスト(距離)
struct Edge* next; // 次のエッジ
} Edge;
Point points[MAXN]; // 地点と交差点を格納
Segment segs[MAXM]; // 線分情報を格納
Edge* graph[MAXN]; // グラフの隣接リスト
int node_count = 0; // 現在のノード数
// 2点が同一かどうかの判定(誤差許容)
int equal(Point p1, Point p2) {
return fabs(p1.x - p2.x) < EPS && fabs(p1.y - p2.y) < EPS;
}
// 2点間のユークリッド距離を計算
double distance(Point p1, Point p2) {
double dx = p1.x - p2.x, dy = p1.y - p2.y;
return sqrt(dx * dx + dy * dy);
}
// 2線分が交差するかを判定し、交点の座標を返す
int intersect(Point p1, Point q1, Point p2, Point q2, double* ix, double* iy) {
double a = q1.x - p1.x;
double b = -(q2.x - p2.x);
double c = q1.y - p1.y;
double d = -(q2.y - p2.y);
double e = p2.x - p1.x;
double f = p2.y - p1.y;
double det = a * d - b * c;
if (fabs(det) < EPS) return 0; // 平行
double s = (d * e - b * f) / det;
double t = (-c * e + a * f) / det;
// 線分の範囲内で交差していなければ無効
if (s < EPS || s > 1 - EPS || t < EPS || t > 1 - EPS) return 0;
*ix = p1.x + s * (q1.x - p1.x);
*iy = p1.y + s * (q1.y - p1.y);
// 端点同士の交差を除外
if (equal((Point){*ix, *iy}, p1) || equal((Point){*ix, *iy}, q1) ||
equal((Point){*ix, *iy}, p2) || equal((Point){*ix, *iy}, q2))
return 0;
return 1;
}
// グラフにエッジを追加(双方向)
void add_edge(int u, int v, double cost) {
Edge* e = malloc(sizeof(Edge));
e->to = v;
e->cost = cost;
e->next = graph[u];
graph[u] = e;
}
// 座標を昇順ソート(x → y)
int cmp_point(const void* a, const void* b) {
Point* p = (Point*)a;
Point* q = (Point*)b;
if (fabs(p->x - q->x) > EPS) return p->x < q->x ? -1 : 1;
if (fabs(p->y - q->y) > EPS) return p->y < q->y ? -1 : 1;
return 0;
}
// ノードのインデックスを取得(新規点は追加)
int get_node_index(Point p) {
for (int i = 0; i < node_count; i++) {
if (equal(points[i], p)) return i;
}
points[node_count++] = p;
return node_count - 1;
}
// グラフ構築:交点の検出と分割、エッジ追加
void build_graph(int M) {
for (int i = 0; i < M; i++) {
Point p1 = points[segs[i].a];
Point p2 = points[segs[i].b];
Point seg_pts[MAXN];
int count = 0;
seg_pts[count++] = p1;
seg_pts[count++] = p2;
// 他の線分との交点を調査
for (int j = 0; j < M; j++) {
if (i == j) continue;
double ix, iy;
if (intersect(p1, p2, points[segs[j].a], points[segs[j].b], &ix, &iy)) {
seg_pts[count++] = (Point){ix, iy};
}
}
// 分割点を並べてソート
qsort(seg_pts, count, sizeof(Point), cmp_point);
// 順にエッジを張る
for (int k = 0; k < count - 1; k++) {
int u = get_node_index(seg_pts[k]);
int v = get_node_index(seg_pts[k + 1]);
double d = distance(seg_pts[k], seg_pts[k + 1]);
add_edge(u, v, d);
add_edge(v, u, d);
}
}
}
// ノードの識別子(地点 or 交差点)をパース
int parse_node(char* s, int N) {
if (s[0] == 'C') { // 交差点
int id = atoi(s + 1);
if (id < 1 || id > node_count - N) return -1;
return N + id - 1;
} else { // 地点
int id = atoi(s);
if (id < 1 || id > N) return -1;
return id - 1;
}
}
// ダイクストラ法による最短経路計算
void dijkstra(int start, double dist[]) {
int used[MAXN] = {0};
for (int i = 0; i < MAXN; i++) dist[i] = INF;
dist[start] = 0;
for (int i = 0; i < node_count; i++) {
int v = -1;
for (int j = 0; j < node_count; j++) {
if (!used[j] && (v == -1 || dist[j] < dist[v])) v = j;
}
if (dist[v] == INF) break;
used[v] = 1;
for (Edge* e = graph[v]; e; e = e->next) {
if (dist[e->to] > dist[v] + e->cost) {
dist[e->to] = dist[v] + e->cost;
}
}
}
}
// メイン関数:入力処理とクエリ応答
int main() {
int N, M, P, Q;
scanf("%d %d %d %d", &N, &M, &P, &Q); // 地点数・線分数・交差点数(未使用)・クエリ数
// 地点の座標を読み込み
for (int i = 0; i < N; i++) {
scanf("%lf %lf", &points[i].x, &points[i].y);
}
node_count = N;
// 線分の情報を読み込み
for (int i = 0; i < M; i++) {
scanf("%d %d", &segs[i].a, &segs[i].b);
segs[i].a--; segs[i].b--;
}
// グラフ構築
build_graph(M);
// クエリ処理
for (int q = 0; q < Q; q++) {
char s1[10], s2[10];
int k; // 未使用
scanf("%s %s %d", s1, s2, &k);
int start = parse_node(s1, N);
int goal = parse_node(s2, N);
if (start == -1 || goal == -1) {
printf("NA\n");
continue;
}
double dist[MAXN];
dijkstra(start, dist);
if (dist[goal] == INF) printf("NA\n");
else printf("%.5f\n", dist[goal]); // 最短距離を出力
}
return 0;
}
自分で試したこと
最短経路の距離については、
6 5 0 5
0 0
2 5
4 7
5 5
7 1
9 5
1 4
1 6
2 5
3 5
4 6
1 4 1
5 6 1
C1 6 1
C1000 1 1
C1 C3 1
と入力したところ、
7.07107
6.10882
5.88562
NA
2.68432
という出力が確認できた。