機械学習に挑戦
いよいよ機械学習の内容に絡めていきましょう!今回は学ぶことも多く、いきなりやるのも酷なので、少しアイスブレイクを入れましょうか。
前回のおさらい(パート2)はこちらから。
イントロダクション
量子コンピュータは、ノーベル物理学賞を受賞していることでも有名な物理学者ファインマンが、「自然現象は量子力学の原理に従っているのだから、自然現象をコンピュータでシミュレーションしたければ、量子力学の原理に従ったコンピュータが必要だ」と提示したことで、量子力学の分野の科学者ドイチュが先陣を切って始めたものだと言われています。
その名の通り、量子と呼ばれるミクロな物質の挙動を参考に作られているわけですが、果たして一体どのようなものか、なるべくわかりやすく説明をしてみようと思います。
そもそも量子とは、非常に小さな粒子のことを指し、例えば酸素分子やその構成単位の酸素原子、またそれを構成する電子、陽子、中性子などがあります。他にも光を波ではなく粒子として見た時の光量子と呼ばれるものもそれに相当しますし(東大はこれをメインにしてますね)、クマムシ君もよく例として挙げられたり実験に使われてたりします。それら量子には共通の性質として、「重ね合わせ」というものがあります。
有名な例え話として、「シュレディンガーの猫」というものがありますね。量子にも、観測するまで「生きている」か「死んでいる」かのような2つの状態が重なることがあります。これを$|0\rangle$と$|1\rangle$に擬えて考えるのです。さて、この「重ね合わせ」こそが量子コンピュータの存在意義そのものであると言えます。簡単に言うと、今までは色々な状態を一つ一つ順に試していかなければいけなかったものを、重ね合わせることで同時並行して試すことができるようになったのです!
これが従来のコンピュータより速く問題を解けると言われる所以で、「量子優位性」と言います。前回扱った「Deutsch-Jozsaのアルゴリズム」でもそれは顕著でしたね。しかしこのアルゴリズムは、考えている関数が定数関数であるかバランス関数であるかを判断するという非常に極端で汎用性に乏しい限定的な条件でのみ活躍するものでした。もっと実用的なものを取り扱って研究したい、おっと、そこに「量子機械学習」があるではないか!
Qiskitの最新モジュール
2021年、新たにIBM社が4つのモジュールをQiskitライブラリに追加しました。
- Qiskit Nature
- Qiskit Finance
- Qiskit Optimization
- Qiskit Machine Learning
昨年秋に行われた "IBM Quantum Challenge Fall 2021" では、この4つの新しいモジュールを使って日常に潜む課題に取り組むことが目的でした。Challengeは全部で4つで、それぞれテーマは、
- 金融
- 化学
- 機械学習
- 最適化
とまさにこれらの新しいモジュールに沿った内容となっていました。
みなさん気になっているとは思います、これらのモジュールをColabで使うにはどうすれば良いかということですが、次のコードをいつもの実行環境の準備の際に追加してください。
!pip install qiskit-nature
!pip install qiskit-finance
!pip install qiskit-optimization
!pip install qiskit-machine-learning
まあ今回は機械学習だけを扱っていく予定なので、最後の一つだけあれば十分です。
"IBM Quantum Challenge Fall 2021" でのChallengeでは、「多クラス分類タスクに対してQSVMを実装し、正確に画像を分類する。」ということが目的でした。MNISTデータセットの亜種であるFashion-MNISTという衣料画像データセットのサブセットからTシャツ、プルオーバー、ドレスの画像を学習し、分類するというものであり、分類であるのでQSVMを考える必要がありました。QSVMとは、サポートベクターマシン(SVM)の量子バージョンですが、一口にQSVMといっても計算の高速化を目指すものと表現力の向上を目指すものがあり、このChallengeでは後者にスポットライトを当てていました。
QMLについて
QML(Quantum Machine Learning)は、量子機械学習の省略形としてよく呼称されます。
2021年、株式会社グリッドの量子アルゴリズム研究チームが、量子機械学習器は過学習しにくいという性質を、詳細な数値実験と統計的機械学習の理論を通して示すことができました(こちらの記事)。過学習とは、機械学習において、訓練データを多く与えすぎることにより学習に偏りが生じ、それ以外の未知のデータに対してパフォーマンスが落ちるというものです。高校生の学生さんにもよくいる「教科書の問題は完璧になったけれど、テストで数値を変えた類題を出したら全くできなくなってしまう」タイプの『事故』ですね。今までは量子機械学習器で過学習は起きにくいのではないかという仮説に過ぎなかったものの、それを今回初めて理論的に説明できたということです。
さて、こんな難しいことは到底自分のレベルではどうにもならないわけですが、今回何をしたいかと言うと、
"IBM Quantum Challenge Fall 2021" の時と同様に計算の高速化ではなく表現力の向上に着目し、「量子SVMと古典SVMの比較」を行いたいと思います。もちろん、古典的な機械学習についても多少なりとも触れる必要があるので、まずはその話から入りましょう!
古典的な機械学習
機械学習というと幅広くなっちゃうので、ここでは主にSVM(サポートベクターマシン)の解説と実装を行います。
SVMとは
まず、SVMとはなんですが、
教師あり学習のクラス分類と回帰のできるアルゴリズム
であり、特徴としては、
- 少ない教師データで高い汎化性能が持てる
- 計算も速く、過学習を起こしづらい
一方で、
- データがばらついたり偏ると、計算量が膨大になる
- 学習が非常に非効率故にデータのサンプル数が多い時、メモリの使用量がバカにならず実行も難しい
というものです。
ここで、「教師あり学習」とは、あるデータとラベルが対になったデータセットを利用し、学習させて未知のデータに適用させるものであり、逆に、「教師なし学習」とは、単に大量のデータだけが与えられ、特徴をもとに学習させるもののことを言います。
教師あり学習の代表例として、以下のようなものがあります。
「分類」
データが属するクラスを予測する、特にクラス数が2の時は2値分類などと言われる。
「回帰」
連続値などを予測する、線形回帰では、与えられたデータをもとに回帰直線を作成し、これを利用して予測する。
また、教師なし学習の代表例として、以下のようなものがあります。
「クラスタリング」
データ間の類似度に基づいてデータをグループ分けする。
「分類」との大きな違いは、「分類」は教師あり学習であり、どのグループに属しているか予め答えがわかっているものから学習するのに対し、「クラスタリング」は、具体的にどのグループに属するかという答えや情報がなく、データごとの特徴を学習するものになっています。
SVMの手法
続いてSVMの手法ですが、次の参考文献から画像を拝借しております。
(SVMとは?Scikit-learnを使ってSVMでクラス分類する方法を解説)
次のように平面上に2種類のデータがあることを仮定しましょう。
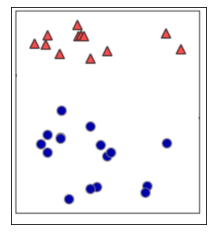
このデータを正しく「分類」できる直線を考えてみたいのです。ここで正しくと言っているのは、単純に考えても赤三角と青丸のグループに分ける直線は無限に存在するわけで、この限られたデータだけから他のものの分布を仮定した一番適した直線を決めたいからです。
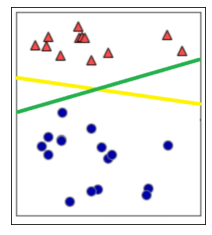
緑の直線も分割できているので一見すると良さそうではあるものの、素人でも黄色の直線の方がデータに沿った直線だと言えますよね。これを直感的なものではなく、理論的に定めてくれるのがSVMとなっています。
その上で、「マージンの最大化」を考えます。マージンとは、線形分離する直線から各々のデータまでの距離のことを指します。
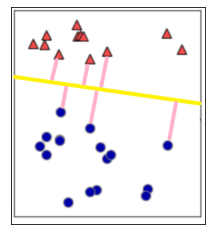
このマージンを最大化するように定めた直線を決めることをマージンの最大化と言います。さて、ある直線からあるデータ(点)までの距離というと、高校数学IIで習う「点と直線の距離」を思い出すことでしょう。
座標平面上の任意の点を$(x_0, y_0)$とし、考えている直線の方程式を$ax + by + c = 0$としたときの、点と直線の距離$d$は、
$d = \frac{\left|{ax_0 + by_0 + c}\right|}{\sqrt {a^2 + b^2}}$
で表せたわけですが、ここで$a$, $b$を要素に持つベクトル$w$を用意します。すなわち、
$w = (a, b)$
と、また、直線の方程式の$x$と$y$についても新しく$x_0$, $x_1$と置き直し
$x = (x_0, x_1)$
とします。更に、便宜上定数$c$を$b$とすると点と直線の距離$d$は
$d = \frac{\left|{w^T \cdot x + b}\right|}{\left|w\right|}$
と改めることができます。ここで$w^T \cdot x$は$w$と$x$の内積を表しています。
このように表すことで、$w$と$x$の次元を$2$以上の整数で任意に取ることができるようになります。次元が$2$であればこれは直線になり、$3$であれば平面を表します。これ以上になると言葉の定義がわからなくなるので、総称してこれを「超平面」などと言います。ここで、ベクトル$w$を「重み」、スカラー定数$b$を「バイアス」と言います。これらには定数倍の任意性があることに注意しましょう(超平面の選び方は自由であるためです)。
与えられたデータの中で、この境界までの距離が一番短いもの、つまり
$ M = \min_k\frac{\left|{w^T \cdot x_k + b}\right|}{\left|w\right|} $
を考えます。今、重みとバイアスには定数倍の任意性があるので
$M = \frac 1{\left|w\right|}$
とします。よって以下を制約条件とすることができるわけです。
$\min_k{\left|{w \cdot x_k + b}\right|} = 1$
さらに、$t_k = \pm 1$($x_k$がラベルAに属するときに$t_k = 1$, ラベルBに属するときに$t_k = -1$)を導入することで制約条件が次のようになります。
$\min_k{\left|{w^T \cdot x_k + b}\right|} = \min_k t_k(w^T \cdot x_k + b) = 1 \Leftrightarrow t_k(w^T \cdot x_k + b) \geq 1$
この条件下で$M$を最大化することを考えれば良いので、ラグランジュの未定乗数法を使いましょう。ここで、$M = \frac 1{\left|w\right|}$を最大化させたいわけですが、これは$\frac1 2 \left|w\right|^2$を最小化する問題に置き換えることができます。これを目的関数として、ラグランジアン$L$は次のようになります。ここで、$\alpha_k$は$0$以上のパラメータとします。
$L = \frac1 2 \left|w\right|^2 - \sum^{n-1}_{k = 0} \alpha_k (t_k(w^T \cdot x_k + b) - 1)$
$\frac{\partial L}{\partial w} = 0 \Rightarrow w = \sum_{k = 0}^{n-1}\alpha_k t_k x_k, \frac{\partial L}{\partial b} = 0 \Rightarrow \sum_{k = 0}^{n-1}\alpha_k t_k = 0$となるので、これを$L$に代入して
$L = \frac1 2 \sum_{k = 0}^{n-1} \sum_{l = 0}^{n-1} \alpha_k \alpha_l t_k t_l {x_k}^T \cdot x_l - \sum_{k = 0}^{n-1} \alpha_k$
となり、$\alpha_k \geq 0, \sum_{k = 0}^{n-1}\alpha_k t_k = 0$の制約下で$L$を最適化する問題に帰着できました!
続いて、「特徴マッピング」について考えていきましょう。ここまでは、境界で完全にラベル毎に分離できる線形分離可能な状況を考えてきました。一方で、どのように境界を設定しても片方のラベルのグループにもう片方のデータが混ざってしまう線形分離不可能な状況を考えなければなりません。そこで重要なのが特徴マッピングです。
次の参考文献から画像を拝借しております。
(機械学習の定番「サポートベクターマシン(SVM)」を高校生でもわかるよう解説)
次のようなデータを考えましょう。
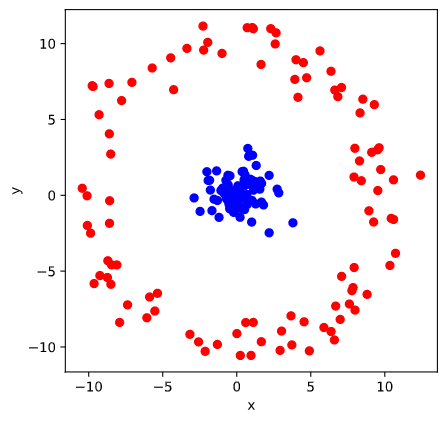
この2種類のデータを$xy$平面上で線形分離することができないのは自明ですね。では、$z = x^2 + y^2$と$z$軸を追加した座標系で考えたらどうでしょうか?
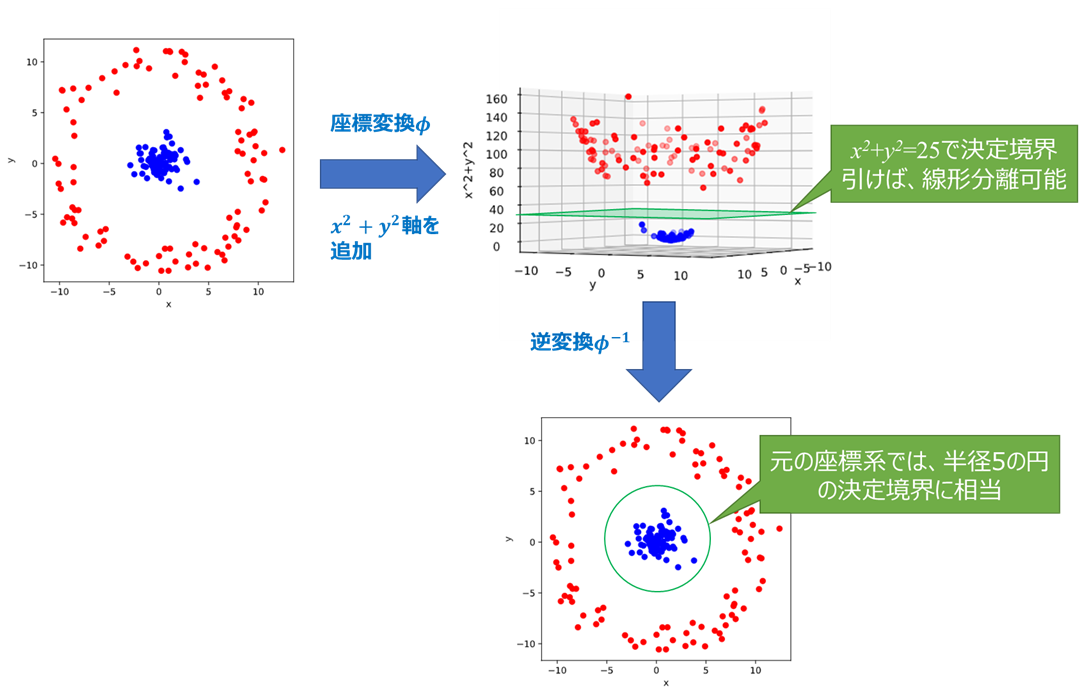
このように、線形分離不可な問題は高次元空間に転写して考えます。これが特徴マッピングです。前に行った議論から、線形分離可能な問題のラグランジアン$L$は次のようになりましたね。
$L = \frac1 2 \sum_{k = 0}^{n-1} \sum_{l = 0}^{n-1} \alpha_k \alpha_l t_k t_l {x_k}^T \cdot x_l - \sum_{k = 0}^{n-1} \alpha_k$
この$x$を座標変換し、$\phi(x)$とすることで$L$は次のように置き換わります。
$L = \frac1 2 \sum_{k = 0}^{n-1} \sum_{l = 0}^{n-1} \alpha_k \alpha_l t_k t_l {\phi(x_k)}^T \cdot \phi(x_l) - \sum_{k = 0}^{n-1} \alpha_k$
しかし、この$\phi(x)$の次元が大きければ大きいほど計算コストも増えるので、一般的にこの$\phi(x)$自体は定義せず、
$K(x_k, x_l) = {\phi(x_k)}^T \cdot \phi(x_l)$
なる関数$K$を定義することが多いです。これを「カーネル関数」と言い、このカーネル関数による変換法を「カーネルトリック」と言います。よく使われるカーネル関数としては以下のようなものがあります。
多項式カーネル
$d$次元以下の全種類の単項式を各成分に持つ特徴量ベクトル$\phi$が対応します。
$K(x_k, x_l) = ({x_k}^T \cdot x_l + c)^d$
ガウスカーネル
無限次元の特徴量ベクトル$\phi$を用いることに等価であり、その中に有用な特徴量も含まれていると期待できます。
$K(x_k, x_l) = \exp(- \frac {\left|x_k - x_l\right|^2} {2\sigma^2})$
シグモイドカーネル
ニューラルネットワークと表層的に類似します。
$K(x_k, x_l) = \tanh(b{x_k}^T \cdot x_l + c)$
SVMの実装
ここからはPythonでどのようにSVMを実装するかのチュートリアルをやってみましょう。線形分離可能なケースは世の中そう多くなく、また線形分離不可であることを仮定しても上手くいくので、いきなり線形分離不可な場合についてやっていきたいと思います。
Scikit-Learnの中の乳癌のデータセットを用いて分類を行います。まずは以下のモジュールをインポートしていきましょう。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
%matplotlib inline
このデータセットの詳細を確認してみましょう。
cancer = load_breast_cancer()
print(cancer.keys())
dict_keys(['data', 'target', 'frame', 'target_names', 'DESCR', 'feature_names', 'filename', 'data_module'])
このように出てきたかなと思います。 'DESCR' はデータの情報を文面で教えてくれます。次のコードで確認してみましょう。
print(cancer.DESCR)
この情報を見ると
Number of Instances: 569
Number of Attributes: 30 numeric, predictive attributes and the class
とあるので、データ数が569で、特徴量が30であることがわかりました。これをチェックするため、 'data' のshapeを見てみましょう。
print(cancer.data.shape)
(569, 30)
と出てきたので大丈夫そうですね。次に、ラベルがどのようになっているかを確認しましょう。
print(cancer.target_names)
'malignant'(悪性)と'benign'(良性)の2種類であることが確認できたので、569個のデータの内、それぞれ何個あるかを見てみます。次のコードを実行しましょう。
print({n: v for n, v in zip(cancer.target_names, np.bincount(cancer.target))})
{'malignant': 212, 'benign': 357}
このように出てきたので、上の 'DESCR' の情報と一致しますね。
さて、ここからはわかりやすいように特徴量とラベルを別の変数に保存しましょう。
X = cancer.data
y = cancer.target
次に、全データを訓練データとテストデータに分割します。次のコードを実行しましょう。
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20)
Scikit-Learnの中にはsvmというライブラリが存在し、ここにある 'SVC(support vector classifier)' というクラスを用います。ここでは引数は1つだけであり、カーネル関数のタイプを決めます。今回は線形分離不可能な場合を仮定しているので、SVMの手法のところでやった3つのカーネル関数「多項式カーネル」、「ガウスカーネル」、「シグモイドカーネル」それぞれに対応するものを順に見てみましょう。
多項式カーネル
svclassifier = SVC(kernel='poly', degree=30)
ガウスカーネル
svclassifier = SVC(kernel='rbf')
シグモイドカーネル
svclassifier = SVC(kernel='sigmoid')
ここに上で任意に抽出した訓練データをフィットさせて学習します。
svclassifier.fit(X_train, y_train)
これで、境界の超平面が決まったことになります。境界を決めて終わりではないので、次にテストデータによってそれが予測したラベルが何なのかを確認します。
y_pred = svclassifier.predict(X_test)
最後に実際のラベルと予測したラベルで正誤判定をします。評価の尺度として、次の3つを考えてみることにしましょう。
| 真のラベル | |||
| 0 | 1 | ||
| 予測ラベル | 0 | $T_0$ | $F_0$ |
| 1 | $F_1$ | $T_1$ | |
上の表の$T_0, F_0, F_1, T_1$を使って
- Accuracy(精度)・・・$0$や$1$と予測したデータのうち、実際にそうであるものの割合
Accuracy = $\frac{T_0 + T_1} {T_0 + F_0 + F_1 + T_1}$
- Precision(適合率)・・・$0$と予測したデータのうち、実際に$0$であるものの割合
Precision = $\frac{T_0} {T_0 + F_0}$
- Recall(再現率)・・・実際に$0$であるもののうち、$0$であると予測されたものの割合
Recall = $\frac{T_0} {T_0 + F_1}$
とします。これを 'evaluation' という関数として定義しましょう。
def evaluation(y_test, y_pred):
accuracy = sum([x == y for x, y in zip(y_pred, y_test)])/len(y_test)
precision = sum([x == y for x, y in zip(y_pred, y_test) if x == 0])/sum([x == 0 for x in y_pred])
recall = sum([x == y for x, y in zip(y_pred, y_test) if y == 0])/sum([y == 0 for y in y_test])
eval_dict = {"Accuracy": np.round(accuracy, 4), "Precision": np.round(precision, 4), "Recall": np.round(recall, 4)}
print(eval_dict)
あとはこれを実行するだけです。
evaluation(y_test, y_pred)
さて、これらをまとめてカーネル関数ごとに比較しやすいようにしましょう。
X = cancer.data
y = cancer.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20)
def evaluation(y_test, y_pred):
accuracy = sum([x == y for x, y in zip(y_pred, y_test)])/len(y_test)
precision = sum([x == y for x, y in zip(y_pred, y_test) if x == 0])/sum([x == 0 for x in y_pred])
recall = sum([x == y for x, y in zip(y_pred, y_test) if y == 0])/sum([y == 0 for y in y_test])
eval_dict = {"Accuracy": np.round(accuracy, 4), "Precision": np.round(precision, 4), "Recall": np.round(recall, 4)}
print(eval_dict)
そして、先ほどと同様に
多項式カーネル
svclassifier = SVC(kernel='poly', degree=30)
svclassifier.fit(X_train, y_train)
y_pred = svclassifier.predict(X_test)
evaluation(y_test, y_pred)
ガウスカーネル
svclassifier = SVC(kernel='rbf')
svclassifier.fit(X_train, y_train)
y_pred = svclassifier.predict(X_test)
evaluation(y_test, y_pred)
シグモイドカーネル
svclassifier = SVC(kernel='sigmoid')
svclassifier.fit(X_train, y_train)
y_pred = svclassifier.predict(X_test)
evaluation(y_test, y_pred)
これでどうでしょうか!実際に実行してみると、シグモイドカーネルの場合のみ著しく性能が低くなっているように見えます。これの原因としては、入力の次元ごとに値のレンジが異なっているため、スケールの違いを上手く吸収できないことが考えられます。入力ベクトルの各次元を平均$0$, 分散$1$に標準化することで性能が上がるのかを検証してみましょう。
from sklearn import preprocessing
X_train_scaled = preprocessing.scale(X_train, axis=0)
X_test_scaled = preprocessing.scale(X_test, axis=0)
svclassifier = SVC(kernel='sigmoid')
svclassifier.fit(X_train_scaled, y_train)
y_pred = svclassifier.predict(X_test_scaled)
evaluation(y_test, y_pred)
他のカーネル関数に引けをとらない正確さを持っていることがわかると思います。
多次元である = 線形分離不可能である、ということではありません。この中で線形分離可能な軸の組み合わせがあれば良いわけです。
import seaborn as sns
df = pd.DataFrame(cancer.data).assign(label=cancer.target)
sns.pairplot(df.iloc[:,[0,1,-1]], hue="label", corner=True)
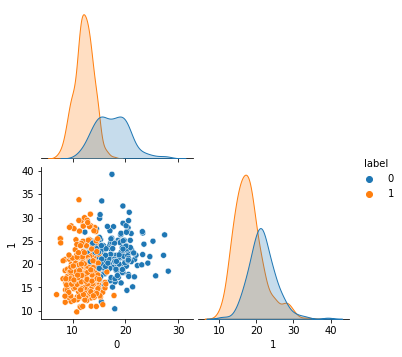
例えば、特徴量の最初の2つを見ると、それなりに線形分離できそうで、実際この部分次元さえあれば他の残りの次元を考える必要はなくなります。この2次元だけを使ってまた同じようにして見てみましょう。
X = cancer.data[:,0:1]
y = cancer.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20)
svclassifier = SVC(kernel='linear')
svclassifier.fit(X_train, y_train)
y_pred = svclassifier.predict(X_test)
evaluation(y_test, y_pred)
ここで、SVCの線形分離可能なものの引数には 'linear' を取ります。
これだけでも、十分ではないものの大幅に間違った結果は出ないことがわかりますね。
長々と古典のSVMについての解説をしてきました、ちょっと疲れてきましたかね。これ以上進むとさすがに重いので今回はこの辺で終わりたいと思います。
次回予告
次回はいよいよ、本当に、QMLを体験してみましょう!
今回の内容が非常に重要なので忘れないように。
パート4はこちらから。