Qiskitであそぼ
某子供向け教育テレビ番組のパクリです。今回はQiskitを使って実際の量子コンピュータの代表的な問題である、「Deutsch-Jozsa(ドイチュ・ジョサ)のアルゴリズム」を取り扱ってみましょう。
前回のおさらい(パート1)はこちらから。
まずは実行環境の準備
!pip install qiskit
!pip install qiskit[visualization]
これでColabでQiskitを動かせますね。続いて諸々のインポートをしましょう。
import numpy as np
from numpy import pi
import math
import matplotlib.pyplot as plt
import qiskit
from qiskit import QuantumCircuit, execute, Aer, IBMQ, ClassicalRegister, QuantumRegister
from qiskit.circuit import Parameter
from qiskit.qasm import pi
from qiskit.tools.visualization import plot_histogram, circuit_drawer
バージョンも確認しましょう。
qiskit.__qiskit_version__
今回は、実機は使わない予定なのでIBM Quantumのアカウントへのアクセスはしません。
Deutsch-Jozsa(ドイチュ・ジョサ)のアルゴリズム
Deutsch-Jozsaのアルゴリズムは、量子コンピュータが得意とする最も典型的な問題についてのものです。
このアルゴリズムは入力変数 {$x_0, ..., x_{n-1}$}$\space\space$($x_i \in$ {0, 1}) を持つ関数 $f(${$x_0, ..., x_{n-1}$}$)$ が定数関数かバランス関数かを判断します。
定数関数
入力変数がどのような値でも、常に$0$または$1$のどちらかを返す関数。
バランス関数
入力変数のとりうる全ての値のうち、丁度半分は$0$を返し、残りの半分については$1$を返す関数。
次のような初期状態を用意します。ただし、$|0\rangle^{{\bigotimes} n}$は$n$個の$|0\rangle$量子ビットを表し、例えば$|0\rangle^{{\bigotimes} 3} = |000\rangle$であるとしましょう。
$|\psi_0\rangle = |0\rangle^{{\bigotimes} n}|1\rangle$
全ての量子ビットに$H$ゲートをかけます。$H$ゲートをかけると、
$|0\rangle → \frac{1}{\sqrt 2}(|0\rangle + |1\rangle)$, $\space\space\space$ $|1\rangle → \frac{1}{\sqrt 2}(|0\rangle - |1\rangle)$
となったので、
$|\psi_1\rangle = H^{{\bigotimes} n+1}|\psi_0\rangle = (\frac{1}{\sqrt 2})^{n+1} (\prod^{n}_{i = 1}(|0\rangle + |1\rangle))(|0\rangle - |1\rangle)$
ここで、 $\prod^{n}_{i = 1}(|0\rangle + |1\rangle) = |00...00\rangle + |00...01\rangle + ... + |11...10\rangle + |11...11\rangle$ なので
$|\psi_1\rangle = (\frac{1}{\sqrt 2})^{n+1} \sum^{2^n-1}_{x = 0}|x\rangle(|0\rangle - |1\rangle)$
と表せます。ただし、$x$には$0$から$2^n-1$までの10進数が入り、例えば$n = 2$のとき、
$\sum^3_{x = 0}|x\rangle = |0\rangle + |1\rangle + |2\rangle + |3\rangle = |00\rangle + |01\rangle + |10\rangle + |11\rangle$
を表しています。
ここに $U_f : |x\rangle|y\rangle → |x\rangle|y \bigoplus f(x)\rangle$ $(\bigoplus : XOR)$ となるようなゲート$U_f$を考えます。この$f(x)$は最初に提示した定数関数かバランス関数か判別したい関数です。ゲート$U_f$はこの関数$f(x)$の情報を持っていて、これを通じて$f(x)$に質問することができます。このような関数$f(x)$をオラクルといい、このオラクルへの質問回数が少ないほど速いアルゴリズムであると言えます。
今、$f(x)$は$0$または$1$を返すはずなので、$XOR$の真理値表から、
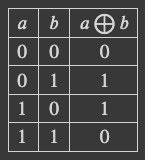
$y = 0$ のとき $→ f(x)$
$y = 1$ のとき $→ 1 \bigoplus f(x) \space\space\space\space\space$ を返します。
また、
$f(x) = 0$ のとき $|f(x)\rangle - |1 \bigoplus f(x)\rangle = |0\rangle - |1\rangle$
$f(x) = 1$ のとき $|f(x)\rangle - |1 \bigoplus f(x)\rangle = |1\rangle - |0\rangle = - (|0\rangle - |1\rangle)$
以上から、状態$|\psi_2\rangle$を次のように定めます。
$|\psi_2\rangle = U_f |\psi_1\rangle =(\frac{1}{\sqrt 2})^{n+1}\sum_{x = 0}^{2^n-1}|x\rangle \space (|f(x)\rangle - |1 \bigoplus f(x)\rangle)$
$\space\space\space\space\space\space\space = (\frac{1}{\sqrt 2})^n\sum_{x = 0}^{2^n-1}(-1)^{f(x)}|x\rangle \frac{1}{\sqrt 2} (|0\rangle - |1\rangle)$
以降、量子ビット$\frac{1}{\sqrt 2} (|0\rangle - |1\rangle)$は必要ないので無視し、残りの$n$量子ビット全てに再び$H$ゲートをかけます。
$|\psi_3\rangle = (\frac{1}{\sqrt 2})^n \sum_{x = 0}^{2^n-1} (-1)^{f(x)} H^{{\bigotimes} n} |x\rangle = (\frac{1}{2})^n \sum_{x = 0}^{2^n-1} (-1)^{f(x)} (\sum^{2^n-1}_{y = 0} (-1)^{x \cdot y} |y\rangle)$
ここで、 $H^{{\bigotimes} n} |x\rangle = (\frac{1}{\sqrt 2})^n \sum^{2^n-1}_{y = 0} (-1)^{x \cdot y} |y\rangle$ という関係を考えます。証明は省略しますが、実例を挙げると、 $|x\rangle = |01011\rangle$ として全てに$H$ゲートをかけると
$|01011\rangle → (\frac{1}{\sqrt 2})^5 (|0\rangle + |1\rangle)(|0\rangle - |1\rangle)(|0\rangle + |1\rangle)(|0\rangle - |1\rangle)(|0\rangle - |1\rangle)$
となるので、ここから作られる$|y\rangle$の係数の正負は$|x\rangle$の$1$である量子ビットの対応を考えれば良いというわけです。
$x = 01011 = x_0x_1x_2x_3x_4, y = y_0y_1y_2y_3y_4$ とします。
$x \cdot y = x_0y_0 \bigoplus x_1y_1 \bigoplus x_2y_2 \bigoplus x_3y_3 \bigoplus x_4y_4 = 0 \bigoplus y_1 \bigoplus 0 \bigoplus y_3 \bigoplus y_4$ と定義することで、 $y_1, y_3, y_4$ の状態によって正負を判断することができるわけです。
$|\psi_3\rangle = \sum_{y = 0}^{2^n-1} [(\frac{1}{2})^n \sum^{2^n-1}_{x = 0} (-1)^{f(x)} (-1)^{x \cdot y}] |y\rangle$
最後に、 $|y\rangle = |0\rangle^{{\bigotimes} n}$ を測定する確率 $Prob(|0\rangle)$ を考えます。このとき、 $x \cdot y = 0$ なので
$Prob(|0\rangle) = \left|(\frac{1}{2})^n \sum^{2^n-1}_{x = 0} (-1)^{f(x)}\right|^2$
$f(x)$が定数関数のとき、$\sum$の中は$2^n$または$-2^n$なので、確率$1$で $|y\rangle = |0\rangle^{{\bigotimes} n}$ が測定されます。反対に$f(x)$がバランス関数のとき、$\sum$の中は半分ずつ$1$と$-1$があるので確率$0$で $|y\rangle = |0\rangle^{{\bigotimes} n}$ が測定されます。
以上より、このアルゴリズムではオラクルへの質問はたったの$1$回で判別できるのです!古典的な方法で解くと(最悪)$2^{n-1}+1$通り試す必要があることを考慮すると、大変早いということがわかりますね。
このアルゴリズムをプログラムするとなると、量子プログラム言語で使用可能なゲートで記述できる必要があります。$U_f$ゲートについて具体的に考えてみましょう。
定数関数のとき、 $f(x) = 0$ であれば$U_f$によって状態が変化することはなかったので、 $U_f = I$ とすれば良く、 $f(x) = 1$ であれば最下位量子ビットに$X$ゲートをかければ良いですね。
バランス関数の方は少しばかり複雑で、$|\psi_1\rangle$の$\sum_{x = 0}^{2^n-1} |x\rangle$に含まれる$x$のうち、 $f(x) = 1$ となる半数の$x$(この集合を$X_1$としておく)については最下位量子ビットが反転するようになれば良く、 $f(x) = 0$ となる残りの半数の$x$($ \in X_0$)については何も変化しないようなゲート$U_f$が必要です。ある量子ビットの状態によって他の量子ビットの状態を操作するので$CX$ゲート($CNOT$ゲート)が適切だと考えられますね。$n = 4$で考えたとき、 $U_f = CX_{0, 4}CX_{1, 4}CX_{2, 4}CX_{3, 4}$ となるゲートが上記を満たします。

このとき、 $x =$ '$0000$' ~ '$1111$'の中で、'$1$'が奇数個含まれる$x$が$X_1$に属します。
では、ようやく以下に具体的なプログラムを構築しましょう。
o = np.random.randint(2) #オラクルを0か1かランダムで決める
if o == 0:
oracle = "c" #0が出たら定数関数(constantのc)
else:
oracle = "b" #1が出たらバランス関数(balanceのb)
Circuit = QuantumCircuit(4 + 1, 4)
Circuit.x(4)
今回は$4$ビットで扱うことにしたいので、必要な量子ビット数は$4 + 1$の$5$量子ビットとなります。$|\psi_0\rangle$の最下位量子ビットは$|1\rangle$であったので、インデックス$4$の量子ビットに$X$ゲートをかけます。
for i in range(4 + 1):
Circuit.h(i)
用意した全ての量子ビットに$H$ゲートをかけましょう。これで$|\psi_1\rangle$ができたことになります。
#オラクルが定数関数のとき
if oracle == "c":
c = np.random.randint(2)
if c == 1:
Circuit.x(4) #f(x) = 1のときは最下位量子ビットにXゲートをかける
else:
Circuit.id(4) #f(x) = 0のときは最下位量子ビットにIゲートをかける
#オラクルがバランス関数のとき
else:
for i in range(4):
Circuit.cx(i, 4) #最下位以外の全ての量子ビットを制御量子ビットとし、最下位量子ビットをターゲット量子ビットにしたcxゲートをかける
最下位以外の量子ビットは元の状態に戻す必要があるので、全てに$H$ゲートをかけ、測定を行います。
for i in range(4):
Circuit.h(i)
for i in range(4):
Circuit.measure(i, i)
Circuit.draw('mpl')
量子回路図は次のようになりました。
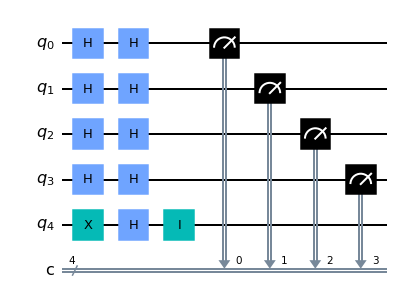
これはもちろん、最初の乱数でオラクルを定数関数とするかバランス関数とするか、また定数関数の場合、$f(x)$が'$0$'か'$1$'かによっても変わってくるので全てのパターンが出てくるか試してみてください(今回は最下位量子ビットに$I$ゲートがかかっていることから、オラクルは定数関数で、$f(x)=0$であることがわかりますね)!
最後に観測結果を表示し、上の議論と正しいか見てみましょう。
backend = Aer.get_backend('qasm_simulator')
results = execute(Circuit, backend=backend, shots=1024).result()
answer = results.get_counts()
print(answer)
plot_histogram(answer)
{'0000': 1024}
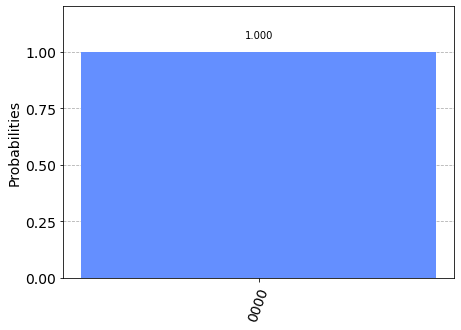
はい、このように出てきたので完璧ですね!
次回予告
次回は「QMLとは?」というところから、従来の機械学習(SVM)についての解説と実装をメインに行います(Qiskitについてはちょびっとだけ)!
いきなりレベルが上がりますが、なるべくわかりやすくをモットーに頑張ります。
パート3はこちらから。