QSVMによる2値分類
量子機械学習の本題に入りましょう。今回は、量子SVMによって2値分類がどのように行われるかを見ていきます。
前回のおさらい(パート3)はこちらから。
肩慣らしの準備
前回の機械学習で忘れてしまいがちですが、QiskitをColabで使えるようにしましょう。早速前回ちょこっとだけ登場した "Qiskit Machine Learning" をインストールしてみましょうか。
!pip install qiskit
!pip install qiskit[visualization]
!pip install qiskit-machine-learning
そしてまた必要(そう)なモジュールのインポートをしていきましょう。
import numpy as np
from numpy import pi
import math
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
from pylab import cm
import warnings
warnings.filterwarnings("ignore")
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler, MinMaxScaler
from sklearn.decomposition import PCA
from sklearn.svm import SVC
import qiskit
from qiskit import QuantumCircuit, execute, Aer, IBMQ, ClassicalRegister, QuantumRegister, BasicAer
from qiskit.circuit import Parameter, ParameterVector
from qiskit.utils import QuantumInstance, algorithm_globals
from qiskit.tools.visualization import plot_histogram, circuit_drawer
from qiskit.circuit.library import PauliFeatureMap, ZFeatureMap, ZZFeatureMap, TwoLocal, NLocal, RealAmplitudes, EfficientSU2, HGate, RXGate, RYGate, RZGate, CXGate, CRXGate, CRZGate
from qiskit_machine_learning.kernels import QuantumKernel
from qiskit_machine_learning.algorithms import QSVC
一応IBM Quantumのアカウントに繋げておきましょうかね。
IBMQ.save_account('*****')
provider = IBMQ.load_account()
provider.backends()
では、楽しい量子機械学習の世界へ行ってらっしゃいませ!
量子教師あり学習
量子教師あり学習として提案されている手法として次のようなものがあります。
「変分量子回路(Quantum Variation Classifier)」
- 特徴空間マッピングを量子状態空間で実行
- 量子回路で予測まで行う(パラメータ最適化は古典)
「量子カーネル推定(Quantum Kernel Estimation)」
- カーネル関数を量子状態の内積として量子回路で再現
- 最終的な予測は古典SVMで実行
2つの手法の違いは次の図で表します。次の参考文献から画像を拝借しております。
(Qiskitで量子SVMを実装して性能評価してみた)

2021年11月16日に、IBM社が127量子ビットの実機の稼働を開始したことがニュースに取り上げられてお祭り騒ぎになりました。しかし、それぞれの量子ビットに対するノイズは十分に取り除くことができないと言われています。そのような量子コンピュータは「NISQデバイス(Noisy Intermediate Scale Quantum device)」と呼ばれます。ある問題が与えられたとき、それを古典コンピュータとNISQデバイス、それぞれの得意分野に2分割することで、ノイズだらけの量子コンピュータでも有効活用できることを示そうという枠組みがあり、それを「古典-量子ハイブリッドアルゴリズム」と言います。上記の2手法がまさにそうです。
せっかく前回カーネル関数についても取り扱ったので、今回は2つ目の量子カーネル推定について考えていこうと思います。
QSVMの概要
量子優位性を使ったSVMがどのようなものかについて見ていきましょう。
量子特徴マップ
マッピングを考える上で重要な量子特徴マップを見ていきます。
前提として古典では表現できないマッピングを考えます。そこで出てくるのが「ヒルベルト空間」です。ヒルベルト空間について、数学的に厳密な定義を知りたい方は各自で調べていただきたいところですが、ここでは簡単に説明しています。
まず、ベクトルが定義できる空間を考え、その中のベクトルの間には加算が定義でき、交換法則、結合法則が成り立ち、スカラー倍の計算が定義され、零元、逆元が存在するとしましょう。凄く簡潔に言うと、計算に困らないものと考えれば良いわけです。これを「ベクトル空間」と言うわけなんですが、更にベクトルとベクトルの間に内積が定義できるとしましょう。内積は簡単に高校数学で習うようなものを考えれば十分です。この空間を「内積空間」と言います。ヒルベルト空間は、この内積空間が「完備性」を持つときのことを指します。完備性を持つとは、コーシー列が収束することを言います。コーシー列とは、集合から好きな要素を取り出して並べた時に、あるところより先の要素を見ると必ず、それらの要素間の距離がどんな狭い範囲にでも収まってしまう、そんなところが必ずある、という並びのことです。長々と文章を連ねていますが、要するにヒルベルト空間は、「複素数の範囲で取り敢えずの計算に困らないベクトル空間」というイメージで良いでしょう。
次の図は、1量子ビットの場合で、これに対応するマッピングはBloch球になります。次の参考文献から画像を拝借しております。
(Supervised learning with quantum enhanced feature spaces)

量子ビットが増えるとより複雑な特徴空間になり、描画できなくなってしまいます。その特徴マッピングのカーネルに対応するのが量子状態の内積であり、
$K(x_k, x_l) = \left|{\langle {\phi(x_k)} | {\phi(x_l)}\rangle}\right|^2$
と表されます。ここで、量子回路の初期状態$|0\rangle^n$から、$|{\phi(x)}\rangle$を作る必要があります。Deutsch-Jozsaのアルゴリズムで行なったことを思い出しましょう。ある状態から別の状態に移すゲート$\mathcal{U}_{\phi(x)}$を$|0\rangle^n$に作用させます。すなわち、
$\mathcal{U}_{\phi(x)}|0\rangle^n = |{\phi(x)}\rangle$
を考えます。量子特徴マップ$\phi(x)$のタイプによって、ゲート$\mathcal{U}_{\phi(x)}$が変わってくることに注意してください。ここでは代表的な量子特徴マップを3つ紹介します。どの特徴マップを使用するかの選択は重要で、扱うデータセットに依存します。
PauliFeatureMap
パウリゲートを駆使した量子特徴マップです。
$\mathcal{U}_ {\phi(x)} = {\prod_d U_{\phi(x)}H^{\otimes n}}, U_{\phi(x)} = \exp\left(i\sum_{S\subseteq[n]}\phi_S(x)\prod_{k\in S} P_i\right)$
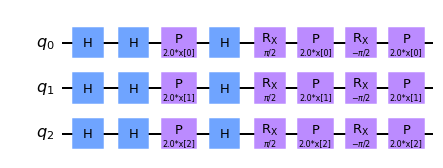
これは以下の回路図に示すように、もつれを生成するブロック$U_{\phi(x)}$と$H$ゲートの層が交互に連なった形をしています。こちらも先ほどの論文から画像を拝借しております。
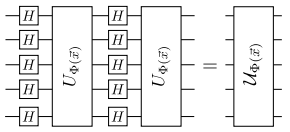
各もつれ生成ブロック$U_{\phi(x)}$の中で、$P_i \in { I, X, Y, Z }$はパウリゲートを表し、添字$S$は量子ビット間の接続に対応しています($S \in {\binom{n}{k},\ k = 1,... n }$)。
これをQiskitで扱うには、以下のコードを実行します。
map_pauli = PauliFeatureMap(feature_dimension=3, reps=1, paulis = ['X', 'Y', 'Z'])
map_pauli.decompose().draw('mpl')
ZFeatureMap
PauliFeatureMapにて、$k = 1, P_0 = Z$のとき、これはZFeatureMapになります。
$\mathcal{U}_ {\phi(x)} = \left( \exp\left(i\sum_j \phi_{{j}}(x) Z_j\right) H^{\otimes n} \right)^d$
ここで$d$は回路の深さ(depth)と呼ばれる量で、増やすことで精度が向上するとされています。しかし、この特徴マップはもつれを伴わないため、古典的なシミュレーションが容易で、量子優位性が得られないことに注意しなければいけません。
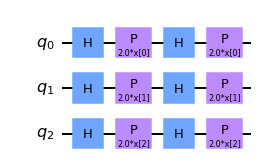
ではこれを扱うコードを実行しましょう。
map_z = ZFeatureMap(feature_dimension=3, reps=2)
map_z.decompose().draw('mpl')
ZZFeatureMap
PauliFeatureMapにて、$k = 2, P_0 = Z, P_1 = ZZ$のとき、これはZZFeatureMapになります。
$\mathcal{U}_ {\phi(x)} = \left( \exp\left(i\sum_{jk} \phi_{{j,k}}(x)Z_j\otimes Z_k\right)\exp\left(i\sum_j \phi_{{j}}(x)Z_j\right)H^{\otimes n} \right)^d$
こちらにはもつれがあるので、より有用なものとなっています。
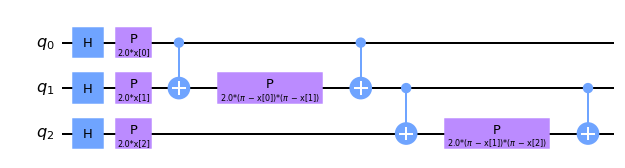
これを扱うコードはいくつかあり、デフォルト(空欄)では引数の "entanglement" は 'full' であり、次のようになります。
map_zz = ZZFeatureMap(feature_dimension=3, reps=1, entanglement='full')
map_zz.decompose().draw('mpl')

線形もつれを考えたければ、引数の "entanglement" を 'linear' として、
map_zz = ZZFeatureMap(feature_dimension=3, reps=1, entanglement='linear')
map_zz.decompose().draw('mpl')
map_zz = ZZFeatureMap(feature_dimension=3, reps=1, entanglement='circular')
map_zz.decompose().draw('mpl')

というようになります。次元数( "feature_dimension" の値)が2のときは、それぞれに違いが起こりません。
量子カーネル推定
続いて、量子カーネル推定について少し細かく見てみましょう。
量子特徴マップ$\phi(x)$から、量子カーネル$K(x_k, x_l) = \left|{\langle {\phi(x_k)} | {\phi(x_l)}\rangle}\right|^2$を考えることができます。これは内積として考えられたものだったので、$x_k$と$x_l$が近いときに大きな値になることから、類似性の尺度として捉えられます。このカーネル行列の各要素は、量子コンピュータ上で遷移確率を測定することにより計算が可能です。
先ほども紹介しました、こちらの論文で議論されているように、量子カーネルに基づくアルゴリズムはその量子カーネルを古典的に推定するのが難しい場合にのみ、古典的な手法に対して優位性をもつ可能性があります。また古典的に量子カーネルを推定することの難しさは、量子優位性を得るための必要条件に過ぎず、十分条件ではありません。
しかし、 A rigorous and robust quantum speed-up in supervised machine learning では、全ての古典的な学習器に対して量子優位性をもつような問題の存在が示されました。
では、実際に前回扱った乳癌のデータを使ってやってみましょう。
from sklearn.datasets import load_breast_cancer
cancer = load_breast_cancer()
X = cancer.data
y = cancer.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20)
これをQSVMによって分類するために、まず値を標準化し、その次元を量子ビットの数(今回は2)まで圧縮(主成分分析)し、-1から1までの間にスケーリングする必要があります。
ss = StandardScaler() #標準化
X_train = ss.fit_transform(X_train)
X_test = ss.transform(X_test)
feature_dim = 2 #主成分分析
pca = PCA(n_components=feature_dim)
X_train = pca.fit_transform(X_train)
X_test = pca.transform(X_test)
mms = MinMaxScaler((-1, 1)) #スケーリング
X_train = mms.fit_transform(X_train)
X_test = mms.transform(X_test)
古典SVMでも扱った 'evaluation' 関数を用意しましょう。
def evaluation(y_test, y_pred):
accuracy = sum([x == y for x, y in zip(y_pred, y_test)])/len(y_test)
precision = sum([x == y for x, y in zip(y_pred, y_test) if x == 0])/sum([x == 0 for x in y_pred])
recall = sum([x == y for x, y in zip(y_pred, y_test) if y == 0])/sum([y == 0 for y in y_test])
eval_dict = {"Accuracy": np.round(accuracy, 4), "Precision": np.round(precision, 4), "Recall": np.round(recall, 4)}
print(eval_dict)
ここまでは、前回とさほど変わりませんね。では、量子優位性を期待できるZZFeatureMapを用いて "QuantumKernel" クラスを設定し、 "statevector_simulator" でカーネル行列を推定します。
ZZ_map = ZZFeatureMap(feature_dimension=feature_dim, reps=3, entanglement='full')
ZZ_kernel = QuantumKernel(feature_map=ZZ_map, quantum_instance=Aer.get_backend('statevector_simulator'))
カーネル行列の1個目と2個目の訓練データ間の遷移確率を算出します。
print(f'First training data : {X_train[0]}')
print(f'Second training data: {X_train[1]}')
First training data : [ 0.70239817 -0.00998021]
Second training data: [-0.69911889 -0.08654478]
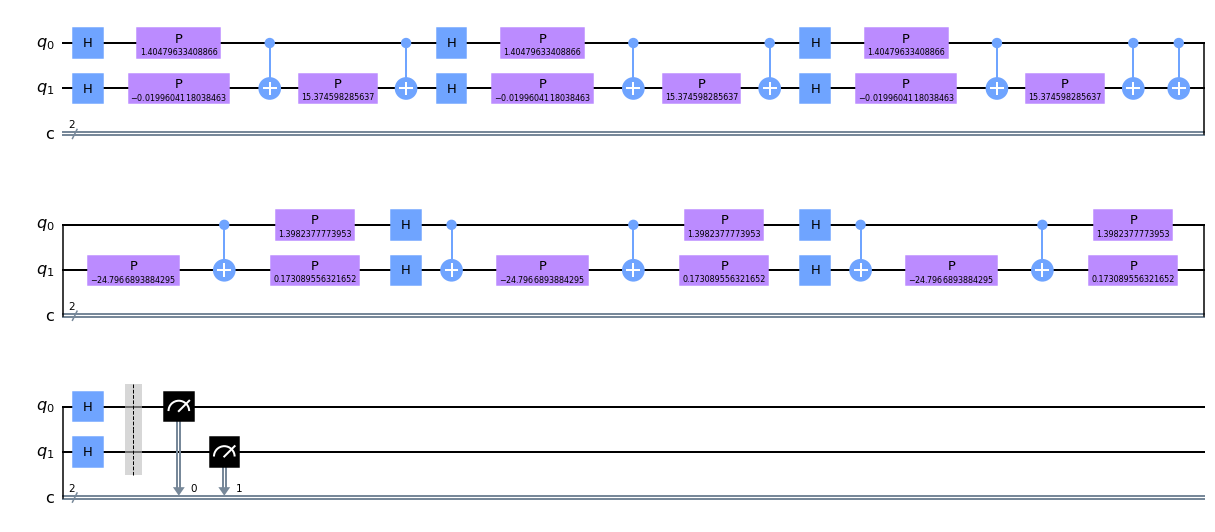
このように出てきました。次に量子回路を作成して描画します。
ZZ_circuit = ZZ_kernel.construct_circuit(X_train[0], X_train[1])
ZZ_circuit.decompose().decompose().draw('mpl')
backend = Aer.get_backend('qasm_simulator')
job = execute(ZZ_circuit, backend, shots=2048)
counts = job.result().get_counts()
plot_histogram(counts)
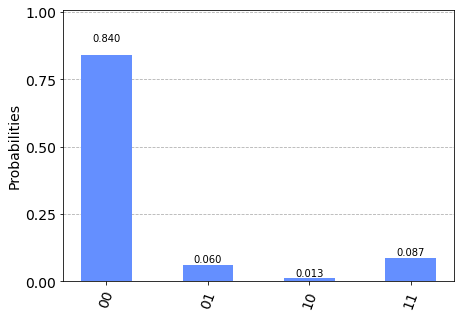
遷移確率は$|0\rangle^2$状態のカウント数の割合として得られます。今回の場合、0.840くらいで出てきます。
print(f"Transition amplitude: {counts['0'*feature_dim]/sum(counts.values())}")
Transition amplitude: 0.84033203125
このようになりましたね。
このプロセスを訓練データの組ごとに繰り返して訓練カーネル行列を埋め、訓練データとテストデータの組ごとに繰り返してテストカーネル行列を埋めます。ここでは、訓練カーネル行列とテストカーネル行列を計算し、プロットしています。
matrix_train = ZZ_kernel.evaluate(x_vec=X_train)
matrix_test = ZZ_kernel.evaluate(x_vec=X_test, y_vec=X_train)
fig, axs = plt.subplots(1, 2, figsize=(10, 5))
axs[0].imshow(np.asmatrix(matrix_train), interpolation='nearest', origin='upper', cmap='Blues')
axs[0].set_title("training kernel matrix")
axs[1].imshow(np.asmatrix(matrix_test), interpolation='nearest', origin='upper', cmap='Reds')
axs[1].set_title("test kernel matrix")
plt.show()
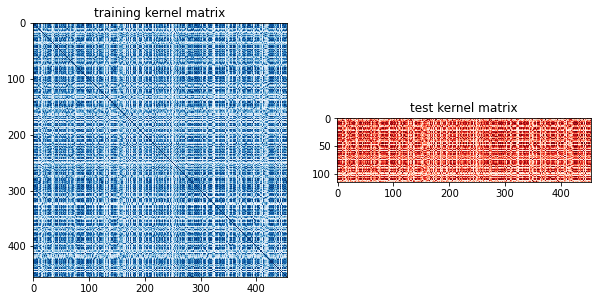
ではいよいよ古典SVMとQSVMの評価を比較してみましょう!まず古典SVMのときにやった手順で、ガウスカーネルを用いて 'evaluation' 関数を動かしてみます。
svclassifier = SVC(kernel='rbf')
svclassifier.fit(X_train, y_train)
y_pred = svclassifier.predict(X_test)
evaluation(y_test, y_pred)
{'Accuracy': 0.9825, 'Precision': 0.9524, 'Recall': 1.0}
このような感じになりました。量子SVMではSVCの引数に "precomputed" とし、svclassifier.fitとsvclassifier.predictの引数を上で計算して出したものに当てはめます。
svclassifier = SVC(kernel="precomputed")
svclassifier.fit(matrix_train, y_train)
y_pred = svclassifier.predict(matrix_test)
evaluation(y_test, y_pred)
{'Accuracy': 0.9386, 'Precision': 0.9714, 'Recall': 0.85}
するとこのように出てきましたね。
ただ、毎回いちいち上のコードを書いてカーネル行列を出してなんてめんどくさいですよね。そこでQiskitには、SVCメソッドに対応する量子のもの、QSVCがあります。そちらで書くとだいぶ短縮したコードで同じものができます。
qsvclassifier = QSVC(quantum_kernel=ZZ_kernel)
qsvclassifier.fit(X_train, y_train)
y_pred = qsvclassifier.predict(X_test)
evaluation(y_test, y_pred)
結果が同じになることを確認してください。
ここまでをまとめると、
from sklearn.datasets import load_breast_cancer
cancer = load_breast_cancer()
X = cancer.data
y = cancer.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20)
ss = StandardScaler()
X_train = ss.fit_transform(X_train)
X_test = ss.transform(X_test)
feature_dim = 2
pca = PCA(n_components=feature_dim)
X_train = pca.fit_transform(X_train)
X_test = pca.transform(X_test)
mms = MinMaxScaler((-1, 1))
X_train = mms.fit_transform(X_train)
X_test = mms.transform(X_test)
def evaluation(y_test, y_pred):
accuracy = sum([x == y for x, y in zip(y_pred, y_test)])/len(y_test)
precision = sum([x == y for x, y in zip(y_pred, y_test) if x == 0])/sum([x == 0 for x in y_pred])
recall = sum([x == y for x, y in zip(y_pred, y_test) if y == 0])/sum([y == 0 for y in y_test])
eval_dict = {"Accuracy": np.round(accuracy, 4), "Precision": np.round(precision, 4), "Recall": np.round(recall, 4)}
print(eval_dict)
ZZ_map = ZZFeatureMap(feature_dimension=feature_dim, reps=3, entanglement='full')
ZZ_kernel = QuantumKernel(feature_map=ZZ_map, quantum_instance=Aer.get_backend('statevector_simulator'))
qsvclassifier = QSVC(quantum_kernel=ZZ_kernel)
qsvclassifier.fit(X_train, y_train)
y_pred = qsvclassifier.predict(X_test)
evaluation(y_test, y_pred)
となります。
さて、もう一度古典のSVMの結果と量子のSVMの結果を照らし合わせてみましょう。
古典 : {'Accuracy': 0.9825, 'Precision': 0.9524, 'Recall': 1.0}
量子 : {'Accuracy': 0.9386, 'Precision': 0.9714, 'Recall': 0.85}
主成分分析をしていることもあり、そもそもの分類の精度が高いのでほぼ誤差に感じます。これだけでは判断しかねないので、超平面がどのように切り分けられたかを可視化してみましょう。次に 'plot_decision_regions' 関数を定義します。これは2次元のデータでどのようにデータが切り分けられているかを可視化してくれる関数になっています。
def plot_decision_regions(X_train, y_train, X_test, y_test, classifier, resolution=0.02):
plt.figure(figsize=(12, 12))
colors = ('blue', 'red')
cmap = ListedColormap(colors[:len(np.unique(y))])
x1_min, x1_max = X_test[:, 0].min() - 0.5, X_test[:, 0].max() + 0.5
x2_min, x2_max = X_test[:, 1].min() - 0.5, X_test[:, 1].max() + 0.5
xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution), np.arange(x2_min, x2_max, resolution))
Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)
Z = Z.reshape(xx1.shape)
plt.contourf(xx1, xx2, Z, alpha=0.4, cmap=cmap)
plt.xlim(xx1.min(), xx1.max())
plt.ylim(xx2.min(), xx2.max())
plt.scatter(X_train[np.where(y_train[:] == 0), 0], X_train[np.where(y_train[:] == 0), 1], marker='s', facecolors='w', edgecolors='b', label="malignant train")
plt.scatter(X_train[np.where(y_train[:] == 1), 0], X_train[np.where(y_train[:] == 1), 1], marker='o', facecolors='w', edgecolors='r', label="benign train")
plt.scatter(X_test[np.where(y_test[:] == 0), 0], X_test[np.where(y_test[:] == 0), 1], marker='s', facecolors='b', edgecolors='w', label="malignant test")
plt.scatter(X_test[np.where(y_test[:] == 1), 0], X_test[np.where(y_test[:] == 1), 1], marker='o', facecolors='r', edgecolors='w', label="benign test")
plt.legend(bbox_to_anchor=(1.05, 1), loc='upper left', borderaxespad=0.)
plt.title("Breast cancer dataset for classification")
plt.show()
まずは古典のものがどのように分けられているかを見てみましょう。
plot_decision_regions(X_train, y_train, X_test, y_test, svclassifier)

次に量子のものがどのように分けられているかを見てみましょう。こちらは少し時間がかかりますね。
plot_decision_regions(X_train, y_train, X_test, y_test, qsvclassifier)
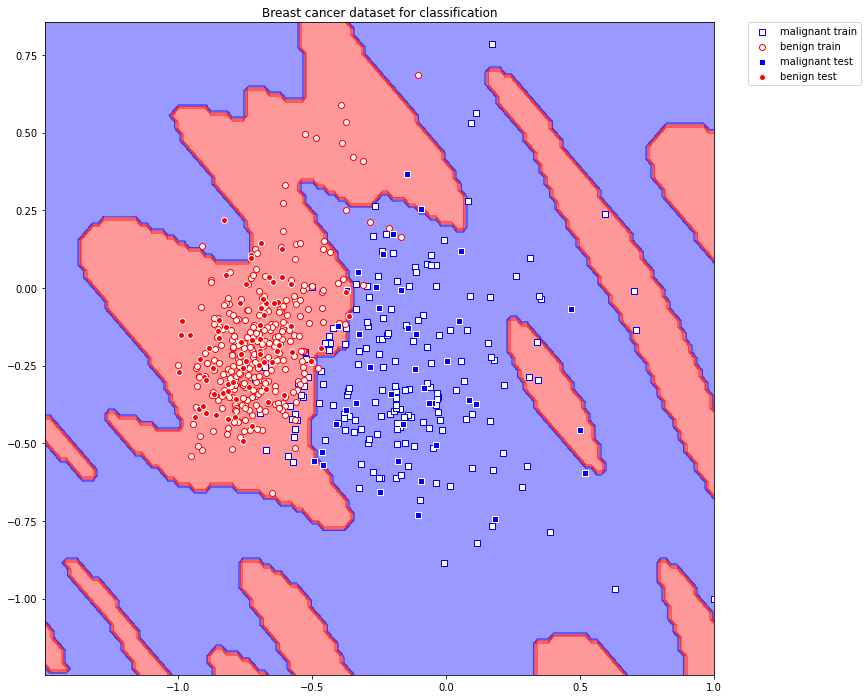
QSVMの方がより複雑な分け方をしているのがよくわかりますね。
ざっとまとめ
QSVMでは古典SVMのカーネル関数に相当するところで、「量子カーネル」というものを使いました。大きな違いはそこだけです。量子特徴マップにも種類があり、扱うデータに依存するため試行錯誤が必要ですね。今回、量子優位性を期待できるZZFeatureMapを扱いました。古典と量子を比較すると、数値的な違いが見られませんでしたが、それはデータそのものが単純なものだったことに起因します。今回わかったこととしては、量子の超平面の切り分け方が古典のものより複雑だということです。これは、古典で正しく分類できなかったデータも、どうにかすれば正しく分類してくれるかもしれないという可能性を秘めているということです。
次回予告
次回最終話となります!最後は3つの実験をしてみます。Scikit-Learnのワインの数値データセットを用いて、3値分類を行うのですが、
- 2つの特徴量で量子SVM、古典SVMそれぞれでできた超平面を可視化し、モデルの性能を評価したものを比較する
- 特徴量を3つに増やし、ZZFeatureMapの中のリピート数、もつれの型の2つのパラメータを変化させてその違いを比較する
- ZZFeatureMapのパラメータを、リピート数4、もつれの型を循環型にフィックスし、特徴量の次元を変えて比較する
という目的でやっていきたいと思うので、乞うご期待を!
パート5はこちらから。