QSVMによる3値分類
いよいよ最後のパートとなります!ここでは、前回予告した通り、Scikit-Learnのワインの数値データセットを用いて、3値分類を行います。
- 2つの特徴量で量子SVM、古典SVMそれぞれでできた超平面を可視化し、モデルの性能を評価したものを比較する
- 特徴量を3つに増やし、ZZFeatureMapの中のリピート数、もつれの型の2つのパラメータを変化させてその違いを比較する
- ZZFeatureMapのパラメータを、リピート数4、もつれの型を循環型にフィックスし、特徴量の次元を変えて比較する
の3本立てですので、一つ一つ検証していきましょう。
前回のおさらい(パート4)はこちらから。
下準備
そろそろ言われなくてもやってますかね?(笑)
!pip install qiskit
!pip install qiskit[visualization]
!pip install qiskit-machine-learning
import numpy as np
from numpy import pi
import math
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
from pylab import cm
import warnings
warnings.filterwarnings("ignore")
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler, MinMaxScaler
from sklearn.decomposition import PCA
from sklearn.svm import SVC
from sklearn.datasets import load_wine
import qiskit
from qiskit import QuantumCircuit, execute, Aer, IBMQ, ClassicalRegister, QuantumRegister, BasicAer
from qiskit.circuit import Parameter, ParameterVector
from qiskit.utils import QuantumInstance, algorithm_globals
from qiskit.tools.visualization import plot_histogram, circuit_drawer
from qiskit.circuit.library import PauliFeatureMap, ZFeatureMap, ZZFeatureMap, TwoLocal, NLocal, RealAmplitudes, EfficientSU2, HGate, RXGate, RYGate, RZGate, CXGate, CRXGate, CRZGate
from qiskit_machine_learning.kernels import QuantumKernel
from qiskit_machine_learning.algorithms import QSVC
ここまでで大丈夫でしょう。それからどうせ全ての実験で必要なので、性能比較用の 'evaluation' 関数も一緒に定義してしまいましょう。
def evaluation(y_test, y_pred):
accuracy = sum([x == y for x, y in zip(y_pred, y_test)])/len(y_test)
precision = sum([x == y for x, y in zip(y_pred, y_test) if x == 0])/sum([x == 0 for x in y_pred])
recall = sum([x == y for x, y in zip(y_pred, y_test) if y == 0])/sum([y == 0 for y in y_test])
eval_dict = {"Accuracy": np.round(accuracy, 4), "Precision": np.round(precision, 4), "Recall": np.round(recall, 4)}
print(eval_dict)
次にワインのデータの詳細を見てみましょう。
wine = load_wine()
print(wine.DESCR)
データ数:178
特徴量:13
ラベル数:3 ('0', '1', '2')
今後、3つ全ての実験において、古典SVMでは「ガウスカーネル」を、量子SVMでは「ZZFeatureMapを使った量子カーネル」を用いて比較します。理由としては、古典においてガウスカーネルが比較的性能が良かったこと、量子においてZZFeatureMapを利用すると量子優位性が期待できたこと、というのがあります。
では、いよいよ実験に参りたいと思います。
実験1
ここでは、「2つの特徴量で量子SVM、古典SVMそれぞれでできた超平面を可視化し、モデルの性能を評価したものを比較する」という実験を行います。2つの特徴量でということなので、13のうちから2つ選んでという意味になります。まずは次のコードを実行します。
X = wine.data[:, [3, 10]]
y = wine.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20, random_state=8192)
ss = StandardScaler()
X_train = ss.fit_transform(X_train)
X_test = ss.transform(X_test)
mms = MinMaxScaler((-1, 1))
X_train = mms.fit_transform(X_train)
X_test = mms.transform(X_test)
ここで、
X = wine.data[:, [3, 10]]
としているのは、4個目の特徴量と11個目の特徴量から判断するということを表しています。お気づきかと思いますが、上のコードではあえて主成分分析をしていません。主成分分析は相関の強い特徴量が選ばれてしまい、古典・量子どちらも精度が高くなり、比較の意義が薄れてしまうからです。今回テキトーに相関が弱そうなものを探していたら、この辺りが良さそうだと思ったのでこのようにしました。
また、以降誰がいつどこでやっても同じ結果をもたらせられるように、 'train_test_split' の引数にて乱数固定をしています。自分は2の13乗が大好きなので、8192としました。
次に、今回の場合における 'plot_decision_regions' 関数を定義しておきましょう。前回とは異なるので注意してください。
def plot_decision_regions(X_train, y_train, X_test, y_test, classifier, resolution=0.02):
plt.figure(figsize=(12, 12))
colors = ('blue', 'red', 'green')
cmap = ListedColormap(colors[:len(np.unique(y))])
x1_min, x1_max = X_test[:, 0].min() - 0.8, X_test[:, 0].max() + 0.8
x2_min, x2_max = X_test[:, 1].min() - 0.8, X_test[:, 1].max() + 0.8
xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution), np.arange(x2_min, x2_max, resolution))
Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)
Z = Z.reshape(xx1.shape)
plt.contourf(xx1, xx2, Z, alpha=0.4, cmap=cmap)
plt.xlim(xx1.min(), xx1.max())
plt.ylim(xx2.min(), xx2.max())
plt.scatter(X_train[np.where(y_train[:] == 0), 0], X_train[np.where(y_train[:] == 0), 1], marker='s', facecolors='w', edgecolors='b', label="0 label train")
plt.scatter(X_train[np.where(y_train[:] == 1), 0], X_train[np.where(y_train[:] == 1), 1], marker='o', facecolors='w', edgecolors='r', label="1 label train")
plt.scatter(X_train[np.where(y_train[:] == 2), 0], X_train[np.where(y_train[:] == 2), 1], marker='^', facecolors='w', edgecolors='g', label="2 label train")
plt.scatter(X_test[np.where(y_test[:] == 0), 0], X_test[np.where(y_test[:] == 0), 1], marker='s', facecolors='b', edgecolors='w', label="0 label test")
plt.scatter(X_test[np.where(y_test[:] == 1), 0], X_test[np.where(y_test[:] == 1), 1], marker='o', facecolors='r', edgecolors='w', label="1 label test")
plt.scatter(X_test[np.where(y_test[:] == 2), 0], X_test[np.where(y_test[:] == 2), 1], marker='^', facecolors='g', edgecolors='w', label="2 label test")
plt.legend(bbox_to_anchor=(1.05, 1), loc='upper left', borderaxespad=0.)
plt.title("Wine dataset for classification")
plt.show()
さて、ある程度準備は整いましたかね。ではこれより比較を行っていきたいと思います。まずは古典SVMから見てみましょう。
svclassifier = SVC(kernel='rbf')
svclassifier.fit(X_train, y_train)
y_pred = svclassifier.predict(X_test)
evaluation(y_test, y_pred)
{'Accuracy': 0.75, 'Precision': 0.75, 'Recall': 0.6667}
このようになりました。これの超平面を描画してみましょう。
plot_decision_regions(X_train, y_train, X_test, y_test, svclassifier)
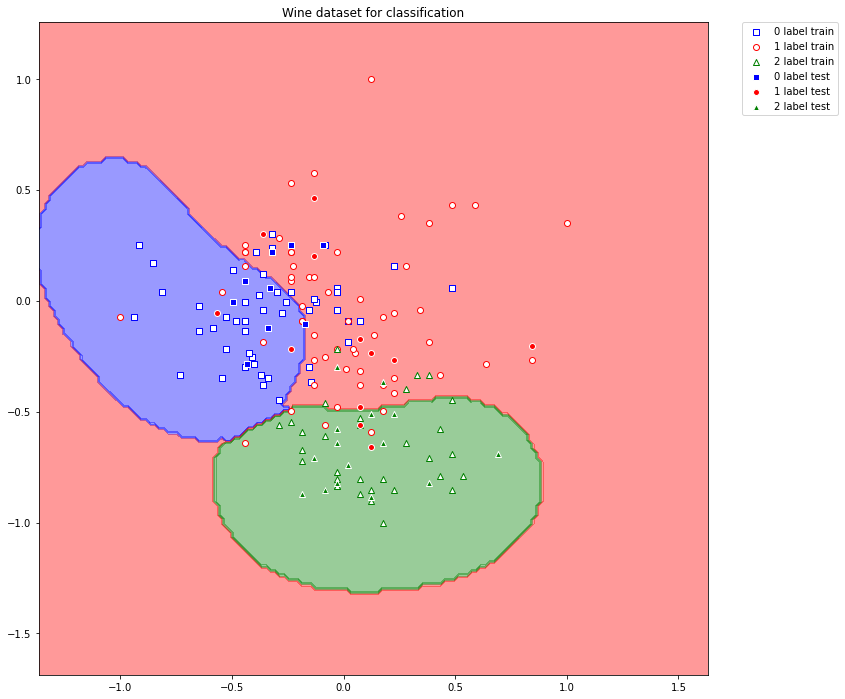
続いて量子の場合についても実行していきましょう。コードは次のようにします。
ZZ_map = ZZFeatureMap(feature_dimension=2, reps=1, entanglement='full')
ZZ_kernel = QuantumKernel(feature_map=ZZ_map, quantum_instance=Aer.get_backend('statevector_simulator'))
qsvclassifier = QSVC(quantum_kernel=ZZ_kernel)
qsvclassifier.fit(X_train, y_train)
y_pred = qsvclassifier.predict(X_test)
evaluation(y_test, y_pred)
{'Accuracy': 0.6389, 'Precision': 0.6, 'Recall': 0.3333}
このようになりました。ここで、リピート数を動かして、どのようになるかを見ていきます。まずは、超平面の変化を見ていきましょう。
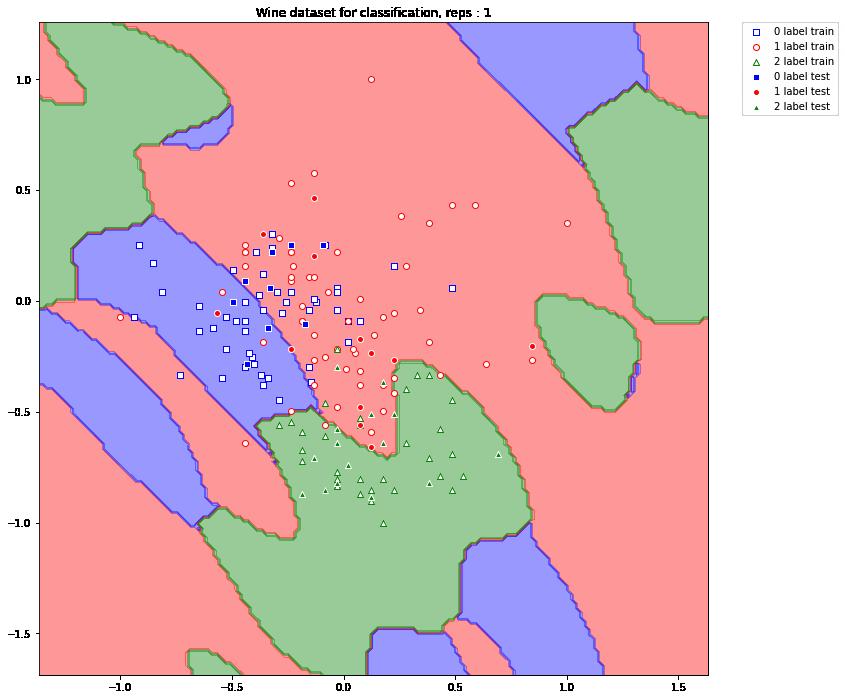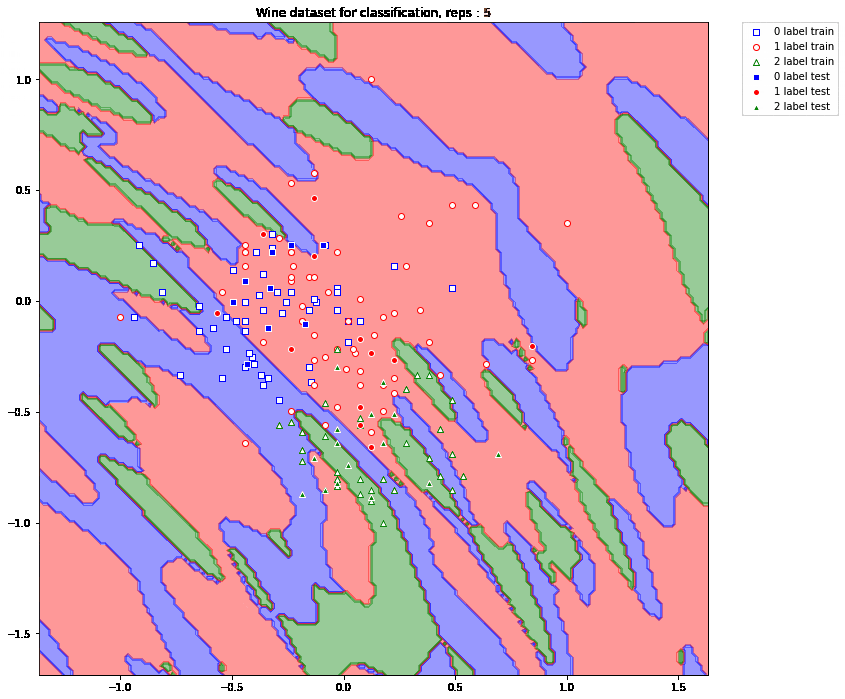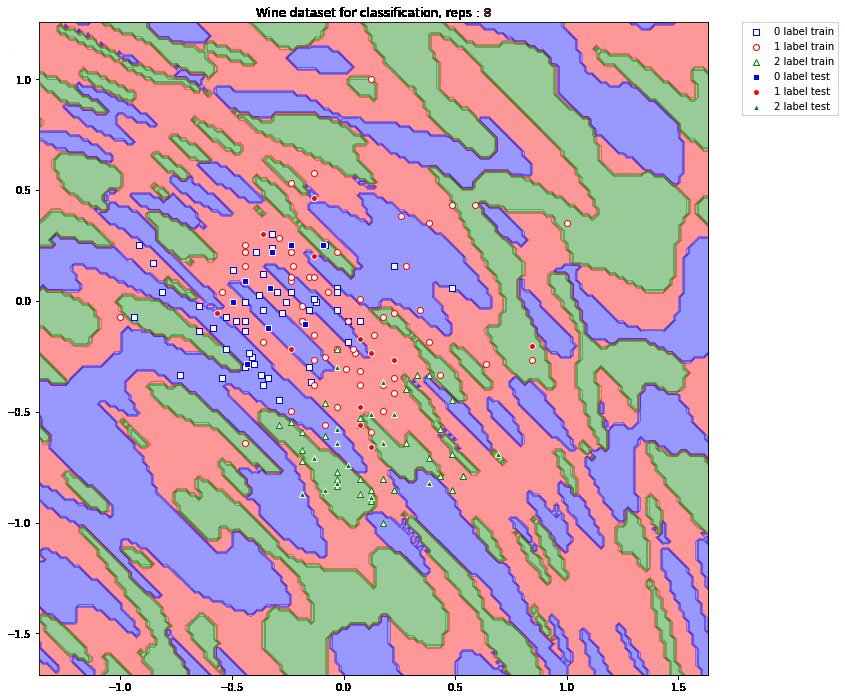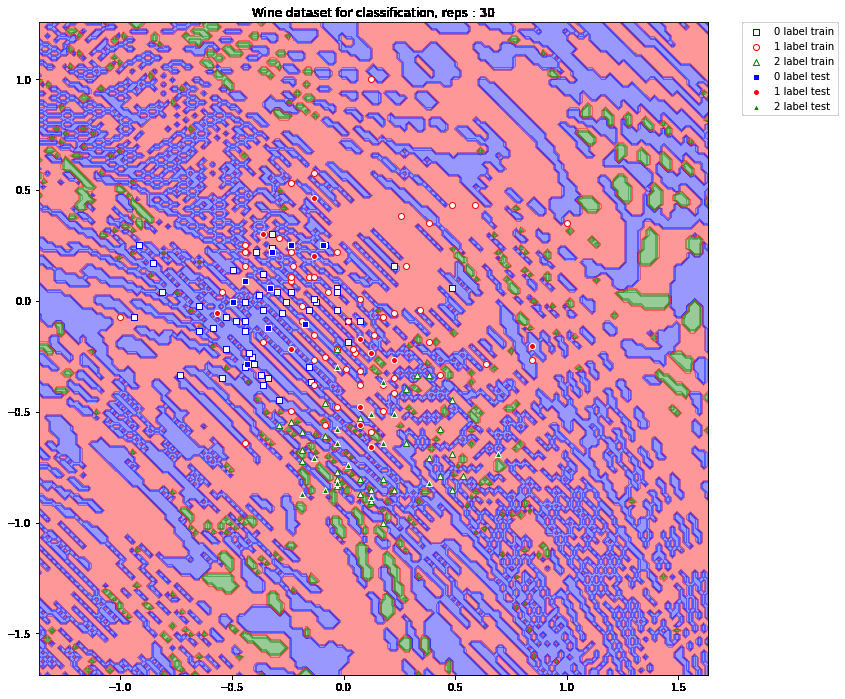
超平面の分け方が複雑化していくのがよくわかりますね。複雑化したことによって正しく分類された点(画面真ん中よりちょっと左斜め上の '0 label test' のデータなど)もあるのではないでしょうか?
続いて、数値評価を見ていきましょう。
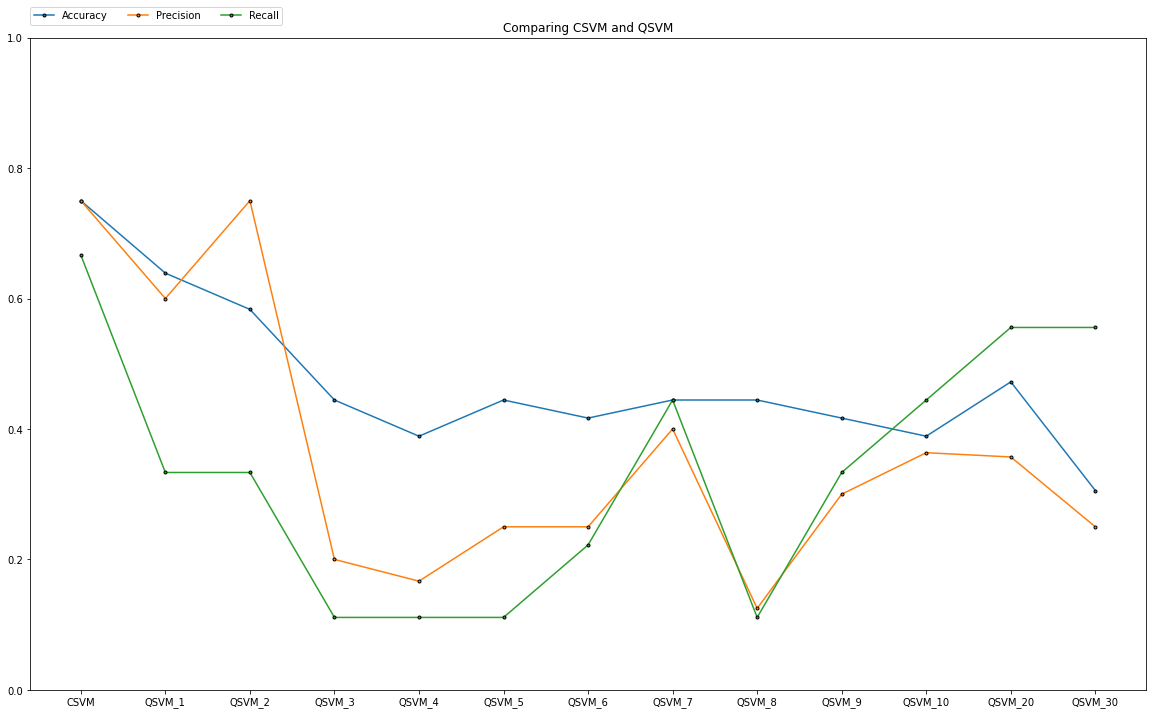
なるほど、決してリピート数が多ければ良いということはないんですね。3つの評価基準もそれぞれ上下に動いているので、こうすれば良い!っていうピッタリなリピート数はなさそうですね。そして大事なこととして、やはり古典のものの正確さには敵わないように思えます。
この実験におけるワインデータセットに対しての結論として、
- リピート数が多くなるほど超平面は複雑化するが、性能は悪くなる傾向にある
- 複雑な超平面によって正しく分類されるようになるデータは存在する
ということが言えます。
実験2
ここでは、「特徴量を3つに増やし、ZZFeatureMapの中のリピート数、もつれの型の2つのパラメータを変化させてその違いを比較する」という実験を行います。特徴量が3つになったので、超平面の可視化は無くなります。前回のパートで軽い紹介に留めましたが、特徴量が3以上になるともつれの型による違いが生まれます。今まで、 'full' でやってきたものを、線形型の 'linear' と循環型の 'circular' の2種類でそれぞれ見ていこうと思います。それでは次の基本コードから、色々見ていきましょう。
X = wine.data[:, [3, 7, 10]]
y = wine.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20, random_state=8192)
ss = StandardScaler()
X_train = ss.fit_transform(X_train)
X_test = ss.transform(X_test)
mms = MinMaxScaler((-1, 1))
X_train = mms.fit_transform(X_train)
X_test = mms.transform(X_test)
特徴量はまた恣意的に、4個目、8個目、11個目で選びました。
svclassifier = SVC(kernel='rbf')
svclassifier.fit(X_train, y_train)
y_pred = svclassifier.predict(X_test)
evaluation(y_test, y_pred)
これは古典のものですね。次の量子のものを、リピート数ともつれの型を変化させてグラフを描いてみましょう。
ZZ_map = ZZFeatureMap(feature_dimension=3, reps=1, entanglement='linear')
ZZ_kernel = QuantumKernel(feature_map=ZZ_map, quantum_instance=Aer.get_backend('statevector_simulator'))
qsvclassifier = QSVC(quantum_kernel=ZZ_kernel)
qsvclassifier.fit(X_train, y_train)
y_pred = qsvclassifier.predict(X_test)
evaluation(y_test, y_pred)
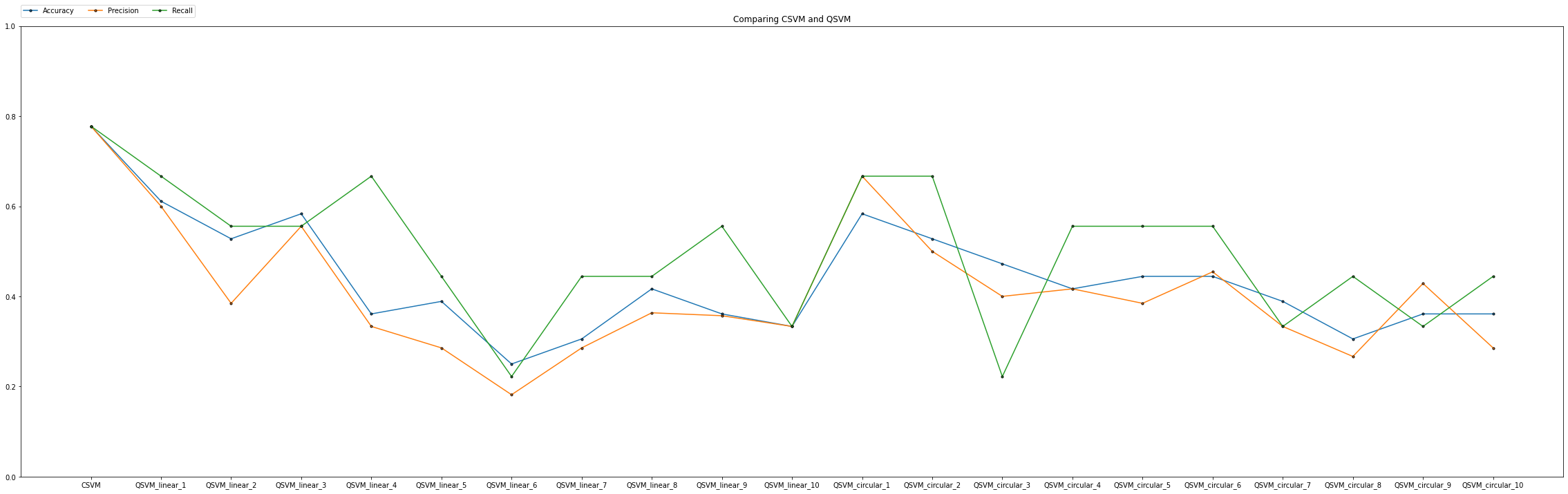
リピート数が多くなるにつれて性能が悪くなる傾向があるのは前実験と同様ですね。今回はもつれの型が変わった時に、どのような差異が出てくるかを確認したかったのですが、上のグラフからはどちらが良いかというのを判断するには難しいですね。
この実験におけるワインデータセットに対しての結論として、
- やはり、リピート数が多くなるほど性能は悪くなる傾向がある
- もつれの型の違いによる決定的な差は視認できない
ということが言えます。
実験3
ここでは、「ZZFeatureMapのパラメータを、リピート数4、もつれの型を循環型にフィックスし、特徴量の次元を変えて比較する」という実験を行います。実験1,2から量子のものより古典のものの方が性能が良さそうなのは明らかでした。今回の実験では、特徴量数の変化で量子SVMの性能の向上を目指し、どれだけ古典のものに近づけるかということを検証してみます。次のコードを見ていきましょう。
X = wine.data[:, [3, 10]]
y = wine.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20, random_state=8192)
ss = StandardScaler()
X_train = ss.fit_transform(X_train)
X_test = ss.transform(X_test)
mms = MinMaxScaler((-1, 1))
X_train = mms.fit_transform(X_train)
X_test = mms.transform(X_test)
svclassifier = SVC(kernel='rbf')
svclassifier.fit(X_train, y_train)
y_pred = svclassifier.predict(X_test)
evaluation(y_test, y_pred)
print()
ZZ_map = ZZFeatureMap(feature_dimension=2, reps=4, entanglement='circular')
ZZ_kernel = QuantumKernel(feature_map=ZZ_map, quantum_instance=Aer.get_backend('statevector_simulator'))
qsvclassifier = QSVC(quantum_kernel=ZZ_kernel)
qsvclassifier.fit(X_train, y_train)
y_pred = qsvclassifier.predict(X_test)
evaluation(y_test, y_pred)
ここから、
X = wine.data[:, [3, 10]]
と
ZZ_map = ZZFeatureMap(feature_dimension=2, reps=4, entanglement='circular')
の部分を変えてみていきます。特徴量は、
[3, 10]→[3, 7, 10]→[1, 3, 7, 10]→[1, 3, 6, 7, 10]→[1, 3, 6, 7, 9, 10]→[1, 2, 3, 6, 7, 9, 10]→[1, 2, 3, 6, 7, 9, 10, 12]
というふうに変えてみました。
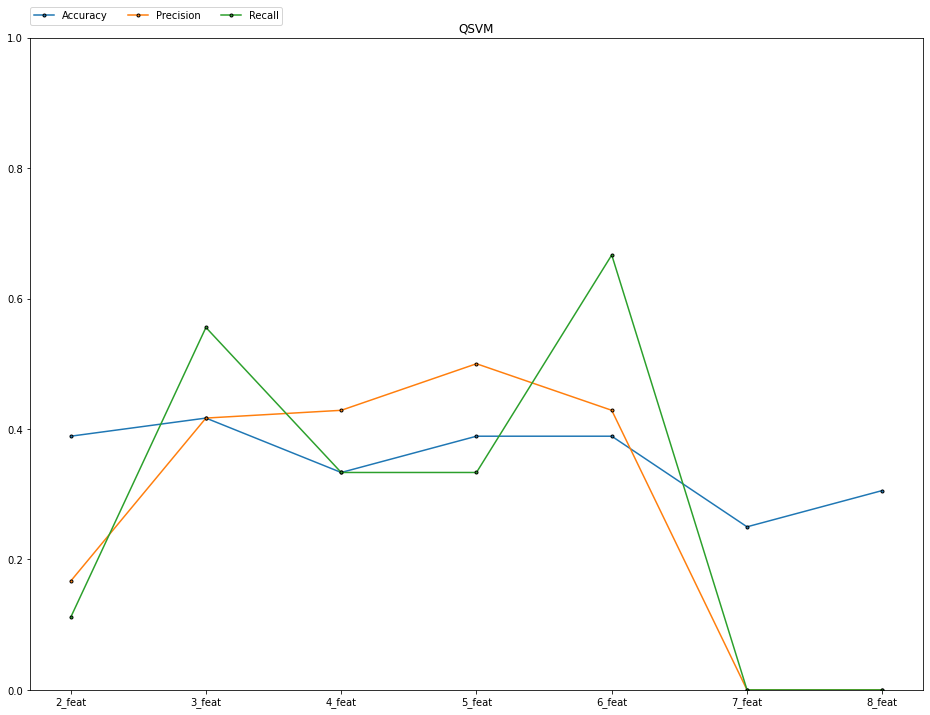
するとこのような変遷を辿りましたね。ちなみに、古典の方は
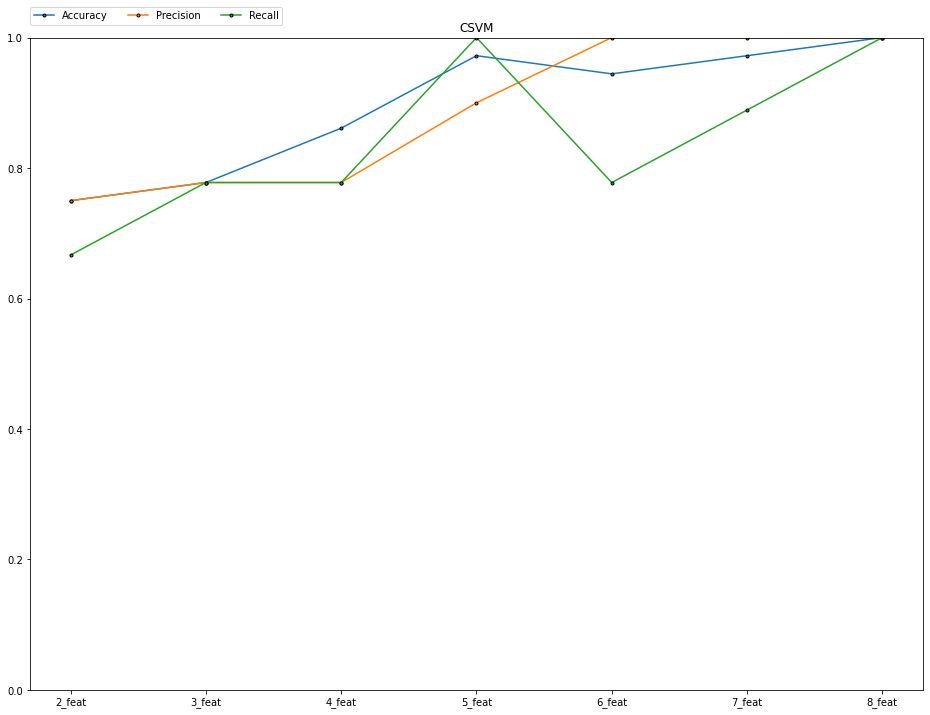
こんな感じになりました。
古典の方は、判断材料となる特徴量が多ければ多いほど性能が良くなっていくのは予想してました。しかし、量子の方は上下変動が激しく、一概にどの場合が良いということは結論が出ず、という感じです。
この実験におけるワインデータセットに対しての結論として、
- 特徴量数が増えるのでもつれの数も増え、不正解の状態ビットの種類が多くなるため、量子SVMの性能は変動すると考えられる
- 特徴量が多い中では、圧倒的に古典SVMの方が性能が良い
ということが言えます。
終わりに
今回の実験からだと、古典SVMの方が圧倒的に性能が良いということになります。そもそも、今回扱っているデータセットがトイモデルなので簡単に分類できてしまい、量子優位性も何も必要ない問題であったということが最初に挙げられるでしょう。量子SVMを実践する見込みは、現在ではまだ薄いでしょう。しかし、例えば、仮により表現力の向上に特化した量子特徴マップが見つかったらどうでしょうか?ZZFeatureMapではなく、もっと優れたマップを選択することで改良できるかもしれません。今後の可能性として、量子SVMの研究には価値があると思います。更に実用的なデータで一般化に繋げられることもあるかもしれませんね。
以上で、「初めてQiskitを使ってからQiskitで量子機械学習ができるようになるまで」のシリーズを完結させていただきます。最後になりますが、本研究のアドバイザーとして協力していただきました、 @ucc_white さん、 @kifumi さん、ありがとうございました!