「ラビットチャレンジ」 提出レポート
1.サポートベクターマシンの概要
■ 2クラス分類のための機械学習手法
■ 線形モデルの正負で2値分類
■ 決定境界はいくつも考えられる
2.サポートベクターマシンの求め方
■ 線形判別関数ともっとも近いデータ点との距離をマージンという
■ マージンが最大となる線形判別関数を求める
■ SVMの主問題について、制約条件付きの最適化問題としてラグランジュ未定乗数法で解くことを考える
■ ラグランジュ未定乗数法
【定義】(引用)

(参考)ラグランジュの未定乗数法の解説と直感的な証明
(参考)ラグランジュの未定乗数法でサポートベクターマシンの主問題を解く
3.ソフトマージンSVM
■ サンプルを線形分離できないとき
■ 誤差を許容し、誤差に対してペナルティを与える
■ マージン内に入るデータや誤分類されたデータに対して誤差を表す変数を導入する
(参考) ソフトマージンSVM
4.非線形分離
■ 線形分離できないとき
■ 特徴空間に写像し、その空間で線形に分離する
5.実装演習1
実施ファイル:np_svm.ipynb
サポートベクターマシン(SVM)
【実施結果】
■ 訓練データ生成① (線形分離可能)

● 学習

● 予測


■ 訓練データ生成② (線形分離不可能)

● 学習
元のデータ空間では線形分離は出来ないが、特徴空間上で線形分離することを考える。
今回はカーネルとしてRBFカーネル(ガウシアンカーネル)を利用する。

● 予測


【考察】
● 線形分離可能データでも、線形分離不可能でデータでも2クラス分類できたことが分かった。(線形分離不可能の場合、特徴空間上で線形分離することを考える)
ソフトマージンSVM
【実施結果】
【考察】
● ソフトマージンSVMは線形分離できない場合でも対応できることが確認できた。(分離不可能な場合は学習できないが、データ点がマージン内部に入ることや誤分類を許容することでその問題を回避する)
6.実装演習2
実施ファイル:skl_svm-checkpoint.ipynb
Titanic Dataset
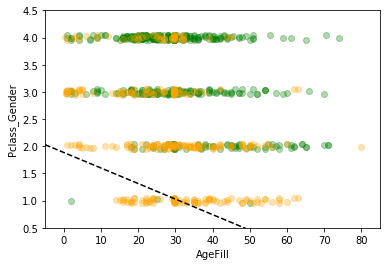
【実施結果】
【考察】
● 線形モデルのSVMの学習は線形カーネルを用いるSVMの学習と同様結果が得られると見える。
● ガウシアンカーネル(RBF)を用いると、上記のグラフから見ると、超学習と見れる。
● 多項式カーネルの場合は良い結果が得られる。
MNIST
【実施結果】
【考察】
● SVMの手法を利用することでは、MNISTの手書き数字データに対して 94% という正解率が得られることが分かった。
IRIS Dataset
【実施結果】
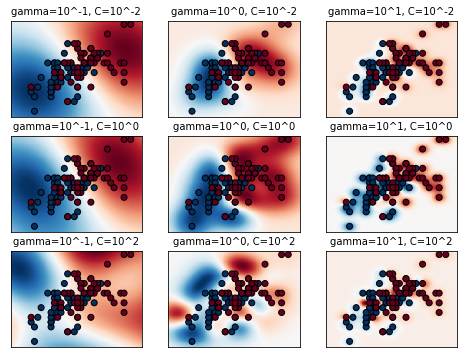
【考察】
● 上のグラフより、パラメータ $C$ の大小で決定境界の形状が変化する。
● $C$の値が大きいと、誤分類のペナルティが大きくなる(誤差許容度が減り)ので、分類境界が細かくなっている。
● もっとも予測精度が高くなるようにパラメータ($C,\gamma$ )を調節する必要がある。
【機械学習】レポート一覧
【ラビットチャレンジ】【機械学習】線形回帰モデル
【ラビットチャレンジ】【機械学習】非線形回帰モデル
【ラビットチャレンジ】【機械学習】ロジスティク回帰モデル
【ラビットチャレンジ】【機械学習】主成分分析
【ラビットチャレンジ】【機械学習】アルゴリズム