はじめに##
ここでは遺伝的アルゴリズムをある程度知っている方向けにgplearnを使った特徴量エンジニアリングの方法を紹介しています。
遺伝的アルゴリズムに触ったことが無い方はこの方のスライドが分かりやすいので概要だけでも理解すると本記事の理解が早くなるかと思います。
遺伝的アルゴリズム(Genetic Algorithm)を始めよう!
(注:筆者は専門家ではありませんので間違いが含まれている可能性がございます。その場合、下のコメントか編集リクエストにて教えて頂けると助かります。なおgplearnはソースも少ないため、殆ど公式ドキュメントを参考にしています。)
目次##
- gplearnとは
- 選択 (Selection)
- 進化 (Evolution)
- 図解
- Symbolic Regressor と Symbolic Transformer
- メトリック
- パラメータ
- その他の細かいこと
- 実装 (Symbolic Transformer)
- 考察
- 参考文献
gplearnとは##
関数同定問題(Symbolic Regression)付きの遺伝的アルゴリズムを使うために開発されたScikit-learnを拡張したライブラリです。
関数同定問題とは抽象的に例えを使って言えば、数々の違った点(x,y)からそれらの点を最も良く表した線(モデル)を探索する回帰分析法の一つです。関数同定問題と言っていますが何かが問題なわけではありません。
具体的に言えば数値空間の関係性を表す数式を特定する回帰分析の一つです。数値空間の関係性を表す数式とは、例えば独立変数aとb, 従属変数yをy=ax+bのように表す数式が挙げられます。これは未知のxからターゲットであるyを予測するために使われます。
よって関数同定問題付きの遺伝的アルゴリズムとは、母集団から数値空間を最も表す数式(個体)を見つけるために繁殖、改変、進化を繰り返すアルゴリズムだと言えます。
ではなぜ数値空間を最も表す数式を見つける必要があるのでしょうか。例えば数式を上手く使えば以下のことができます。ここに特徴量(x1,x2,x3)があったとしましょう。そのうちのx2を取り除きます。そして残った(x1,x3)を使ってx2を最も表す(説明する)数式を見つけます。そしてその数式を見つけたら、そこに実際にx2を当てはめます。するとx2ではないですが、x2に近い新しい特徴量が生まれます。これを変数x、3つ分繰り返してみます。すると特徴量(x)の合計は6つになります。これは後で説明するSymbolic Regressorというモデルで行うことができます。
ちなみにgplearnで扱う数式は足し算や引き算からsin、cos、変数や定数などが含まれています。これらを組み合わせたものを(遺伝的アルゴリズムの)個体とし、各々の個体が各々の数値空間を表します。そして最終世代の中に残った個体から最も数値空間を表す個体を抽出します。
それではまず最初にgplearn内の一つ一つの個体が数式をどのように格納しているかについて話します。
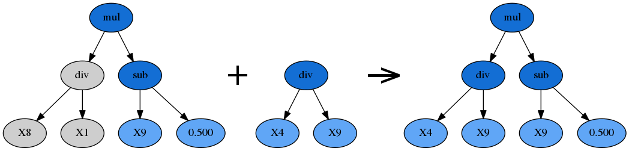
例として次のような式を挙げます。
X_0^2 - 3X_1 + 0.5 = 0 \\
Numpyではこのように表せます。
y = np.add(np.subtract(np.multiply(X0, X0), np.multiply(3., X1)), 0.5)
構文木で表すと次のようになります。
濃い青のノードが関数、水色のノードが変数と定数です。
左下から計算すれば上述の式を表すことができます。
gplearnではこの関数、変数、定数をlistに格納します。
具体的には次のような数式に変換してから格納しています。
y=+-×X_0X_0×3X_10.5 \\
突然意味が分からなくなりましたね。順を追って説明します。まず、
y=X_0^2 - 3X_1 + 0.5 = 0 \\
という式は
y=X_0X_0 - 3X_1 + 0.5 = 0 \\
と表せますが、LISPで使われるS式と呼ばれるデータ構造表現ではこう書けます。
y=(+(-(×X_0X_0)(×3X_1))0.5) \\
括弧の一番内側から計算すると、
y=(+(-(X_0^2)(3X_1))0.5) \\
となり
y=(+(X_0^2-3X_1)0.5) \\
となっていくのがわかります。
先ほどの構文木の左下から徐々に計算していくイメージです。
gplearnではS式の括弧を全て取り除いてListに格納しています。
ちなみにgplearnでは推測器(Estimator)を初期化するときに引数を通して利用できる関数を指定します。以下が指定できる関数の一覧です。
‘add’ : addition, arity=2.
‘sub’ : subtraction, arity=2.
‘mul’ : multiplication, arity=2.
‘div’ : division, arity=2.
‘sqrt’ : square root, arity=1.
‘log’ : log, arity=1.
‘abs’ : absolute value, arity=1.
‘neg’ : negative, arity=1.
‘inv’ : inverse, arity=1.
‘max’ : maximum, arity=2.
‘min’ : minimum, arity=2.
‘sin’ : sine (radians), arity=1.
‘cos’ : cosine (radians), arity=1.
‘tan’ : tangent (radians), arity=1.
arityというのは引数を幾つ取るかを表しています。例えば足し算ならadd(引数1,引数2)となるのでarity=2です。
実際のコードで表すと、まずfunction_setという配列を初期化します。そしてその配列をgplearnのオブジェクト生成時に引数として渡します。
function_set = ['add', 'sub', 'mul', 'div',
'sqrt', 'log', 'abs', 'neg', 'inv',
'max', 'min', 'sin', 'cos', 'tan']
gp = SymbolicRegressor(function_set=function_set, population_size=1000,
verbose=1, generations = 5, metric='mse',
random_state=0, n_jobs=-1)
もし自身の関数を定義したいのなら[functions.make_function()]
(https://gplearn.readthedocs.io/en/stable/reference.html#gplearn.functions.make_function)を使います。
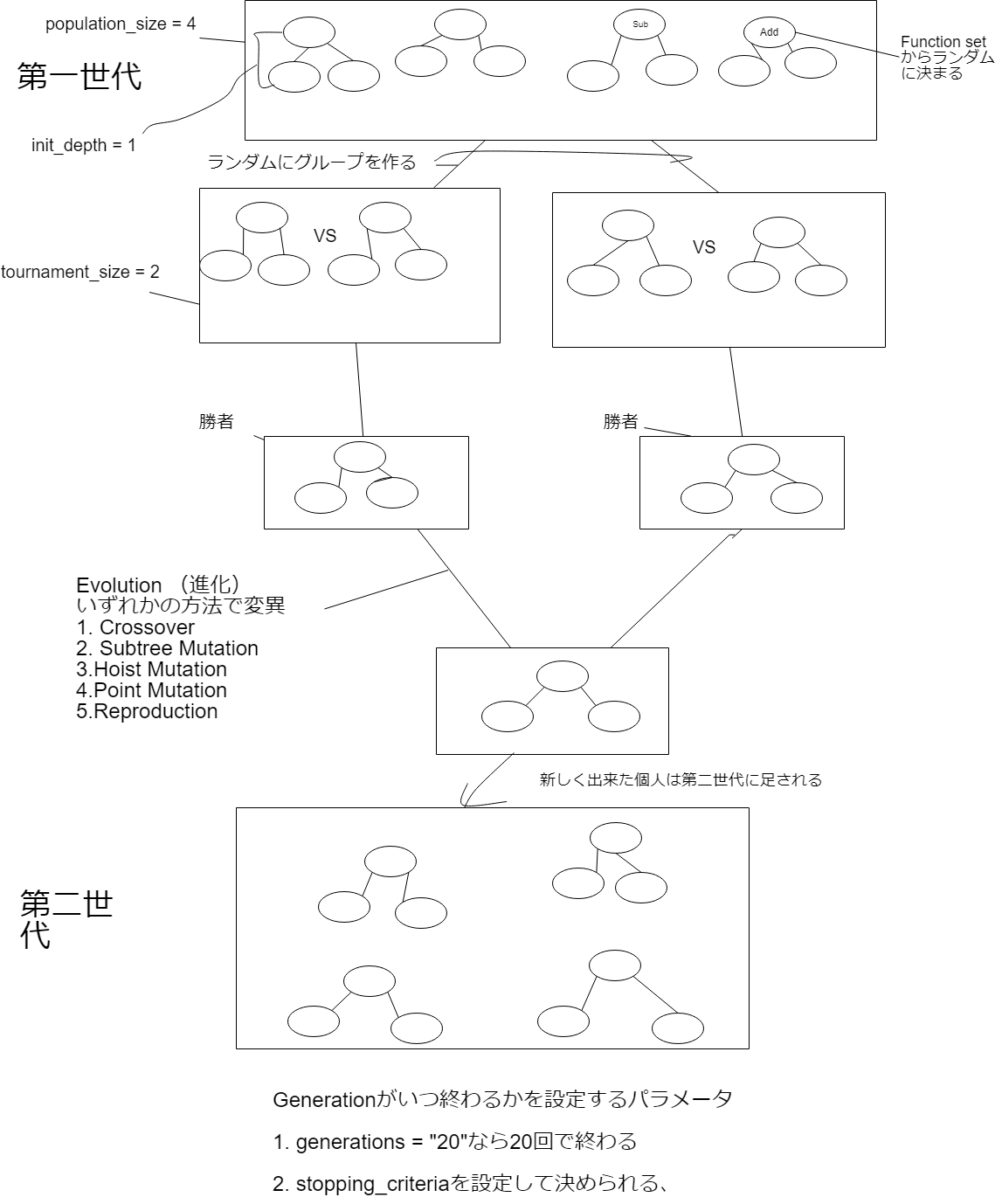
選択 (Selection)
gplearnでは選択はトーナメント方式を採用しています。トーナメント方式とは「予め決めた個体数(トーナメントサイズ)をランダムに抽出し、その中で最も適応度の高い個体を選択する方式」です。
tournamen_sizeというパラメータで設定ができます。トーナメントサイズが大きければ最適化された数式を早く見つけ、小さければ(大きくしたときよりも)より良い数式を見つけられる可能性が上がります。なぜならそれだけ時間をかけて個体を選び進化させるからです。
このtournament_sizeの設定はプログラムのコンピューティングにかかる時間とのトレードオフとなりそうです。
進化 (Evolution)
gplearnではいくつかの進化(変異)形式がサポートされています。
-
Crossover
-
Subtree Mutation
-
Hoist Mutation
-
Point Mutation
-
Reproduction
-
Crossover
二つの違ったグループでトーナメントを行い、そこで勝ち上がってきた二つの個体(構文木)からランダムに部分木を抽出し組み合わせます。組み合わせるときにどちらかが親(根本の木)になり、どちらかがドナーになります。Crossoverのパラメーターはp_crossoverです。
- Subtree Mutation
Subtree Mutationでは、1つのグループでトーナメントを行い勝ち上がった個体(構文木)から部分木を取り、それを親とします。そしてランダムに生成した部分木(ドナー)を親に付け加えます。Crossoverのドナー側がランダムに作られた部分木に変わったイメージです。
Subtree Mutationのパラメータはp_subtree_mutationで決めます。
- Hoist Mutation
Hoist Mutationとは、1つのグループでトーナメントを行い勝ち上がった個体(構文木)からランダムに部分木を取ります。その部分木から、さらにランダムに部分木を取りそれを繰り上げます。下の図では0.5を繰り上げしています。そして次の世代で0.5のノードは子孫を新たに作ります。
- Point Mutation (最も使われる)
Point Mutationとは1つのグループでトーナメントを行い勝ち上がった個体(構文木)からランダムにノードを選び、そのノードを他のランダムに選ばれたノードと入れ替えます。
ノードが関数の場合は別の関数に、ノードが定数や変数の場合は別の定数や変数に置き換えられます。p_point_replaceというパラメータで入れ替えのノード数を調整します。
- Reproduction
1つのグループでトーナメントを行い、勝ち上がった個体をそのまま変えずに次の世代に渡します。
図解##
適当に作ったので少々荒々しいですがご了承ください。理解を促すためにシンプルに作りました。init_depthは2つパラメータを取り(1, 3)の場合1から3の間の数字を取るということで、全てが図のようにinit_depth=1になるわけではありません。図で間違いがありましたら教えて頂けると有難いです。
Symbolic Regressor と Symbolic Transformer##
gplearnには主に二つのモデルがあります。一つ目がSymbolic Regressorで二つ目がSymbolic Transformerです。Symbolic TransformerはSymbolic Regressorと少し違います。Symbolic Regressorは出力したyとターゲットとして決めたyを比較し(yやターゲットのyは変数xでも構わない)、そのエラーを最小化しようとするのに対し、Symbolic Transformerは出力したyとターゲットとして決めたyの相関性(Correlation)を最大化しようとします。これは相関性の無いプログラムに相関性を与えるために行われます。言い換えればSymbolic regressorは損失を最小化しようとするのに対し、Symbolic Transoformerは決定係数(coefficient of determination)であるr^2を最大化しようとします。r^2とは従属変数であるxを使って独立変数であるyをどの程度表現(説明)できるかを0から1の間で表した数字です。
コードの違いとしてはSymbolic Regressorではpredict()で新しい特徴を生成するのに対し、Symbolic Transformerはtransform()で新しい特徴を生成します。
Symbolic Transformerは決定係数を使うと述べましたが、Transformerを通したあとにランダムフォレストやブースティング等のツリーベースモデルを推測器として使う場合はスピアマンの相関係数を使います。逆に線形モデル(linear model)の場合は、統計で頻繁に使われるピアソンの積率相関係数(r)を使います。スピアマンだとかピアソンだとかの計算方法は覚える必要は無くて、自分の使う機械学習アルゴリズムに合わせて、パラメータをスピアマンかピアソンのどちらかに変えれば良いと思います。私もスピアマンの方は勉強していないのでよく分かりません(笑)コード内ではSymbolic Transformerのオブジェクト生成時にmetricというパラメータで'pearson'か'spearman'に設定できます。
パラメータについてですがSymbolic Transformerで注目すべきはhall_of_frameです。Symbolic Transformerは最終世代から最も適応した(決定係数r^2が高い)個体から最も適応性が低かった個体までを(n_components分だけ)出力します。n_componentsのパラメータは同じような個体を削ぎ落す役割があります。例えば決定係数の高さがトップの似たような個体が2つあるときそのうちの1つを除外します。
またプログラム実行後に_best_programsを使えばhall_of_frameの中に入っていた_Program(個体)オブジェクトを最も関連性があったものから無かったものまで(n_components分)listで出力できます。
例えばhall_of_frame=100でn_components=10のとき、print(gp._best_programs)にすると(最終世代の中から最もがあったものから無かったものまで)、10個のオブジェクト(個体)が確認できます。
[<gplearn._program._Program object at 0x000001B4800D8390>, <gplearn._program._Program object at 0x000001B4FDDC7D30>, <gplearn._program._Program object at 0x000001B480845B00>, <gplearn._program._Program object at 0x000001B4800C8710>, <gplearn._program._Program object at 0x000001B480A826D8>, <gplearn._program._Program object at 0x000001B4FE4CC7F0>, <gplearn._program._Program object at 0x000001B4FDCD2EB8>, <gplearn._program._Program object at 0x000001B4FDEF95F8>, <gplearn._program._Program object at 0x000001B48071E390>, <gplearn._program._Program object at 0x000001B4FDE39390>]
そのうちの一つ目のオブジェクトの中身を print(gp._best_programs[0])で確認すると、最初の章で説明したS式で格納されていることが確認できます。
inv(sqrt(div(X10, mul(X5, inv(sqrt(div(add(-0.646, X10), mul(X11, mul(X5, mul(X5, mul(X5, mul(X5, inv(X12)))))))))))))
他にも便利な表示機能が公式ドキュメントに載ってます。
メトリック (Metrics)
遺伝的アルゴリズムではプログラム(個体)の精度を適応度(Fitness)として測ります。機械学習で言えば損失やスコアと同じようなものです。gplearnでは平均二乗誤差(mse)や平均平方二乗誤差(rmse)が用意されています。
またfitness.make_fitness()を使えば適応度を測る関数を自身で作れます。
gplearnではmseとrmseしかサポートされていないので、自分のモデルに合わせて適応度を測る関数を作ることが多いようです。
(Symbolic Transformerではpearson か spearman)
基本パラメータ##
init_depth: 一番最初の世代の構文木の深さ。その後の各世代の深さは進化によって変わる。
population_size: 各世代の初期化人口。特徴量が豊富なときや大きなプログラムを動かすときは大き
く設定する必要あり。デフォルトは1000
metric:
Symbolic Regressor: mse か rmse
Symbolic Transformer: pearson か spearman
その他の細かいこと##
-
機械学習でもそうですが、例えば1を0又は0に限りなく近い数で割ると答えが∞になりエラーを起こしてしまいます。gplearnではそのようなことを防ぐためにクロージャ(関数閉包)を使っています。一言でいえば独自の関数でエラーが起きないように制御しています。例えば分母が-0.001 から 0.001になったときにはエラーが起きないように1として計算を行います。
-
質の高い遺伝的アルゴリズムを作るためにはパラメータに気を付ける必要があります。理由として例えばyの変数が500から1000の値を取っていて、変数であるxが-1から0を取るような値であった場合、定数を0.5に設定するのは好ましくありません。なぜなら遺伝的アルゴリズムは500~1000の範囲に近づけるために意味のないような足し算を延々と続けるからです。
これと同じようにデータを標準化したりスケーリングすることは質の高いプログラムを作るうえで重要です。
3.遺伝的アルゴリズムには肥大化(Bloat)という問題があります。これは適応度が改善されていないにも関わらず構文木のノード、すなわち要素が増えていくことを指します。これはparsimony_coefficientというパラメータで抑制できます。具体的にはトーナメント時に構文木の要素数に比例して適応度を下げます。これにより適応度は同じ程度だが要素数が極端に違う個体がいた場合、要素数が少ない方が選ばれます。数式がシンプルな個体と数式が長ったらしい個体が居て同じ程度の適応度だったら前者を選びますよね。
実装##
ここではまず最初にgplearnのドキュメントで紹介されているBoston housing dataを使ってSymbolic Transformerで特徴量エンジニアリングをしてみます。そしてlightgbmでエンジニアリング前と後の結果を比べます。
その後前のTensorflowとTFlearnの記事で使ったデータをここでも使って実際に特徴量エンジニアリングを行いLightgbmで比較します。
前記事のデータはsuperdatascience.comのPart1からダウンロードできます。churn_model.csvという名前です。
1. Boston Housing Data###
まずはTransformerを使って特徴量を生み出しr^2(決定係数)を改善しましょう。先にも述べましたが決定係数を改善することで、よりxがyを説明(表現)できるようにします。
import numpy as np
import pandas as pd
import lightgbm as lgb
from sklearn.linear_model import Ridge
from sklearn.model_selection import KFold
from sklearn.utils import check_random_state
from sklearn.datasets import load_boston
from sklearn.metrics import roc_auc_score, accuracy_score, mean_squared_error
from gplearn.genetic import SymbolicTransformer, SymbolicRegressor
from gplearn.fitness import make_fitness
from statistics import mean
from math import sqrt
if __name__ == '__main__':
rng = check_random_state(0)
boston = load_boston()
perm = rng.permutation(boston.target.size)
boston.data = boston.data[perm]
boston.target = boston.target[perm]
est = Ridge()
est.fit(boston.data[:300, :], boston.target[:300])
print(est.score(boston.data[300:, :], boston.target[300:]))
function_set = ['add', 'sub', 'mul', 'div',
'sqrt', 'log', 'abs', 'neg', 'inv',
'max', 'min']
gp = SymbolicTransformer(generations=20, population_size=2000,
hall_of_fame=100, n_components=10,
function_set=function_set,
parsimony_coefficient=0.0005,
max_samples=0.9, verbose=1,
random_state=0, n_jobs=3)
gp.fit(boston.data[:300, :], boston.target[:300])
gp_features = gp.transform(boston.data)
new_boston = np.hstack((boston.data, gp_features))
est = Ridge()
est.fit(new_boston[:300, :], boston.target[:300])
print(est.score(new_boston[300:, :], boston.target[300:]))
print(gp._best_programs[0])
結果は以下の通り
0.75931945305
| Population Average | Best Individual |
---- ------------------------- ------------------------------------------ ----------
Gen Length Fitness Length Fitness OOB Fitness Time Left
0 11.04 0.33987636199 6 0.822502090604 0.675124281718 15.58s
1 6.91 0.593562307154 7 0.836993346084 0.60246769713 19.02s
2 5.07 0.730092647095 8 0.840630478099 0.704016759154
(省略).............................................................................
19 21.69 0.697116437372 24 0.888272483674 0.560249626654
0.841837210518
inv(sqrt(div(X10, mul(X5, inv(sqrt(div(add(-0.646, X10), mul(X11, mul(X5, mul(X5, mul(X5, mul(X5, inv(X12)))))))))))))
決定係数(r^2)が0.75931945305から0.841837210518になり相関性が高まったことが分かります。
最も適応力の高かった数式(個人) gp._best_programs[0]
inv(sqrt(div(X10, mul(X5, inv(sqrt(div(add(-0.646, X10), mul(X11, mul(X5, mul(X5, mul(X5, mul(X5, inv(X12)))))))))))))
それではlightgbmを使って結果を比較します。
import numpy as np
import pandas as pd
import lightgbm as lgb
from sklearn.linear_model import Ridge
from sklearn.model_selection import KFold
from sklearn.utils import check_random_state
from sklearn.datasets import load_boston
from sklearn.metrics import roc_auc_score, accuracy_score, mean_squared_error
from gplearn.genetic import SymbolicTransformer, SymbolicRegressor
from gplearn.fitness import make_fitness
from statistics import mean
from math import sqrt
if __name__ == '__main__':
rng = check_random_state(0)
boston = load_boston()
perm = rng.permutation(boston.target.size)
boston.data = boston.data[perm]
boston.target = boston.target[perm]
function_set = ['add', 'sub', 'mul', 'div',
'sqrt', 'log', 'abs', 'neg', 'inv',
'max', 'min']
gp = SymbolicTransformer(generations=20, population_size=2000,
hall_of_fame=100, n_components=10,
function_set=function_set,
parsimony_coefficient=0.0005,
max_samples=0.9, verbose=1,
random_state=0, n_jobs=3)
gp.fit(boston.data[:300, :], boston.target[:300])
gp_features = gp.transform(boston.data)
boston.data = np.hstack((boston.data, gp_features))
params = {
'objective':'regression',
'max_depth':-1,
'n_estimators':100,
'learning_rate':0.1,
'colsample_bytree':0.3,
'num_leaves':8,
'metric':'auc',
'n_jobs':-1
}
folds = KFold(n_splits=5, shuffle=False, random_state=2019)
print('Light GBM Model')
acc = list()
for fold_, (trn_idx, val_idx) in enumerate(folds.split(boston.data, boston.target)):
print("Fold {}: ".format(fold_+1))
reg = lgb.LGBMRegressor(**params)
reg.fit(boston.data[trn_idx], boston.target[trn_idx], eval_set=[(boston.data[val_idx], boston.target[val_idx])], verbose=0, early_stopping_rounds=500)
y_pred = reg.predict(boston.data[val_idx])
acc.append(sqrt(mean_squared_error(boston.target[val_idx], y_pred) ** 0.5))
print(mean(acc))
検証前のRMSE: 2.9854797050365036
検証後のRMSE: 2.9106607780366494
0.07エラーが少なくなっているのが確認できます。
2.前記事のデータ (Churn_Modeling)###
まずはTransformerを使ってr^2(相関性)を高めてみます。
# ライブラリ省略
def pre_processing(data):
x = data.iloc[:, 3:13].values
y = data.iloc[:, 13].values
label_encoder_x_1 = LabelEncoder()
x[:, 1] = label_encoder_x_1.fit_transform(x[:, 1])
label_encoder_x_2 = LabelEncoder()
x[:, 2] = label_encoder_x_2.fit_transform(x[:, 2])
onehotencoder = OneHotEncoder(categorical_features = [1])
x = onehotencoder.fit_transform(x).toarray()
x = x[:, 1:]
return x, y
def scaling(x):
sc = StandardScaler()
x = sc.fit_transform(x)
return x
if __name__ == '__main__':
data = pd.read_csv('data.csv')
x, target = pre_processing(data)
x = scaling(x)
NUM = 7000
est = Ridge()
est.fit(x[:NUM, :], target[:NUM])
print('Before: ' + str(est.score(x[NUM:, :], target[NUM:])))
function_set = ['add', 'sub', 'mul', 'div',
'sqrt', 'log', 'abs', 'neg', 'inv',
'max', 'min', 'sin', 'cos', 'tan']
gp = SymbolicTransformer(generations=20, population_size=2000,
hall_of_fame=100, n_components=10,
function_set=function_set,
parsimony_coefficient=0.0005,
max_samples=0.9, verbose=1,
random_state=0, n_jobs=3,
metric='spearman')
gp.fit(x[:NUM, :], target[:NUM])
gp_features = gp.transform(x)
x = np.hstack((x, gp_features))
est = Ridge()
est.fit(x[:NUM, :], target[:NUM])
print('After: ' + str(est.score(x[NUM:, :], target[NUM:])))
結果
Before: 0.138827856659
| Population Average | Best Individual |
---- ------------------------- ------------------------------------------ ----------
Gen Length Fitness Length Fitness OOB Fitness Time Left
0 9.15 0.0716912029927 4 0.372365664308 0.350000407222 39.53s
1 6.24 0.19449188607 14 0.388155235439 0.417715204988 41.08s
2 3.61 0.293752671946 7 0.410432749326 0.374194440262 41.47s
(省略).............................................................................
19 27.19 0.380070635863 25 0.523245420905 0.400815001481 0.00s
After: 0.32247970836
Transformerを使ってr^2が0.138827856659から0.32247970836になりました。かなり良さそうな結果です。ではこれをlightgbmに当てはめて結果を比較します。
# ライブラリ省略
# pre_processing関数とscaling関数を省略
if __name__ == '__main__':
data = pd.read_csv('data.csv')
x, target = pre_processing(data)
x = scaling(x)
NUM = 7000
function_set = ['add', 'sub', 'mul', 'div',
'sqrt', 'log', 'abs', 'neg', 'inv',
'max', 'min', 'sin', 'cos', 'tan']
gp = SymbolicTransformer(generations=20, population_size=2000,
hall_of_fame=100, n_components=10,
function_set=function_set,
parsimony_coefficient=0.0005,
max_samples=0.9, verbose=1,
random_state=0, n_jobs=3,
metric='spearman')
gp.fit(x[:NUM, :], target[:NUM])
gp_features = gp.transform(x)
x = np.hstack((x, gp_features))
params = {
'objective':'binary',
'max_depth':5,
'n_estimators':200,
'learning_rate':0.1,
'colsample_bytree':0.3,
'num_leaves':8,
'metric':'auc',
'n_jobs':-1
}
folds = KFold(n_splits=5, shuffle=False, random_state=2019)
print('Light GBM Model')
acc = list()
for fold_, (trn_idx, val_idx) in enumerate(folds.split(x, target)):
print("Fold {}: ".format(fold_+1))
clf = lgb.LGBMClassifier(**params)
clf.fit(x[trn_idx], target[trn_idx], eval_set=[(x[val_idx], target[val_idx])], verbose=0, early_stopping_rounds=500)
y_pred_test = clf.predict_proba(x[val_idx])
y_pred_k = np.argmax(y_pred_test, axis=1)
acc.append(accuracy_score(target[val_idx], y_pred_k))
print(mean(acc))
特徴エンジニアリング前のAccuracy:0.8662
特徴エンジニアリング後のAccuracy:0.8616
相関性を高めることはできましたが、残念ながら結果は少し低くなりました。パラメータを色々いじりましたが、解決には及ばず。
色々調べてみた結果、kaggleでregressorで試している方を見かけたのでSymbolic regressorで試してみました。
このコードでは一つの特徴をyとし、他の特徴をxと設定してます。そして他の特徴xから特徴yを予想しその値を新しい特徴として追加しています。これを特徴量分forで繰り返します。(gplearnとは?の章で説明するために用いた例えの実装です。(x1,x2,x3)のやつ)
import numpy as np
import pandas as pd
import lightgbm as lgb
from sklearn.linear_model import Ridge
from sklearn.model_selection import KFold
from sklearn.utils import check_random_state
from sklearn.preprocessing import LabelEncoder, OneHotEncoder
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import roc_auc_score, accuracy_score
from gplearn.genetic import SymbolicTransformer, SymbolicRegressor
from gplearn.fitness import make_fitness
from statistics import mean
def pre_processing(data):
x = data.iloc[:, 3:13].values
y = data.iloc[:, 13].values
label_encoder_x_1 = LabelEncoder()
x[:, 1] = label_encoder_x_1.fit_transform(x[:, 1])
label_encoder_x_2 = LabelEncoder()
x[:, 2] = label_encoder_x_2.fit_transform(x[:, 2])
onehotencoder = OneHotEncoder(categorical_features = [1])
x = onehotencoder.fit_transform(x).toarray()
x = x[:, 1:]
return x, y
def scaling(x):
sc = StandardScaler()
x = sc.fit_transform(x)
return x
if __name__ == '__main__':
data = pd.read_csv('data.csv')
x, target = pre_processing(data)
x = scaling(x)
function_set = ['add', 'sub', 'mul', 'div',
'sqrt', 'log', 'abs', 'neg', 'inv',
'max', 'min', 'sin', 'cos', 'tan']
gp = SymbolicRegressor(function_set=function_set, population_size=1000,
verbose=1, generations = 5, metric='mse',
random_state=0, n_jobs=-1)
store_x = np.zeros((x.shape[0],x.shape[1]))
col = x.shape[1]
for i in range(col) :
trn_x = np.delete(x,i,1)
trn_y = x[:,i]
gp.fit(trn_x, trn_y)
store_x[:,i] = gp.predict(trn_x)
x = np.hstack((x, store_x))
params = {
'objective':'binary',
'max_depth':5,
'n_estimators':200,
'learning_rate':0.1,
'colsample_bytree':0.3,
'num_leaves':8,
'metric':'auc',
'n_jobs':-1
}
folds = KFold(n_splits=5, shuffle=False, random_state=2019)
print('Light GBM Model')
acc = list()
for fold_, (trn_idx, val_idx) in enumerate(folds.split(x, target)):
print("Fold {}: ".format(fold_+1))
clf = lgb.LGBMClassifier(**params)
clf.fit(x[trn_idx], target[trn_idx], eval_set=[(x[val_idx], target[val_idx])], verbose=0, early_stopping_rounds=500)
y_pred_test = clf.predict_proba(x[val_idx])
y_pred_k = np.argmax(y_pred_test, axis=1)
acc.append(accuracy_score(target[val_idx], y_pred_k))
print(mean(acc))
結果
特徴エンジニアリング前のAccuracy:0.8662
特徴エンジニアリング後のAccuracy:0.8655
ここでも元々0.8662から0.8655に落ちました(笑)Transformerを使ったときよりはマシになりましたがエラーは改善されませんでした。実装自体は未だ色々と試してないのでまだ改善点があると思われます。Optunaを使ってチューニングもしたり、一部だけ特徴を除いてgplearnしてみるのもありですね。
とりあえずはここまでとして、また色々と試して分かったことがあったら随時この記事を更新します。
もし何か知っている方がいましたら教えて頂けると有難いです。
考察(今の時点)##
1.パラメータを色々試す必要があるかもしれない(この記事ではコンピュテーションに時間がかからないように大きすぎるパラメータは設定していなかった。)
2.データセットによってアプローチの仕方を変える必要性あるかもしれない。データの量、特徴の数、回帰問題なのか、分類問題なのか。データは相関し合っているか、し合っていないのか。既に精度は十分なものなのか、不十分なのか。色々と考える余地がありそうです。
参考文献##
https://gplearn.readthedocs.io/en/stable/index.html
https://gplearn.readthedocs.io/en/stable/examples.html
https://www.kaggle.com/pnussbaum/santander-genetically-engineered-features-v07