前回のクォターニオンとは?でやったことは、クォターニオンの回転が四次元空間上の「直行する2つの平面の回転の合成」であるということだ。そして今回はそれぞれの平面での回転を実際に計算する予定だった。
しかし四次元回転は2つの平面の回転角の大きさによっていくつか種類に分類される。そこでまずは、重要だと思った4次元回転の種類を紹介する。
ここからは難解な部分もあるが、順を追って理解していけば問題なく理解できる。
Simple Rotation → Isoclinic Rotation → (Double Rotation)の順がいい。
四次元回転の種類
四次元空間における回転は、二つの平面を平面A,平面Bとした場合、それぞれの平面の回転の値によって特性が変わってくる。四次元回転が2つの平面での回転での合成であるのならば、それはなんとなく予想できるだろう。実はそれぞれの平面での回転の組み合わせのパターンに応じて特性が違うことから、それらのパターンには名前がついている。重要なパターンを紹介しよう。
平面Aでの回転をα、平面Bでの回転をβとすると
Simple Rotation
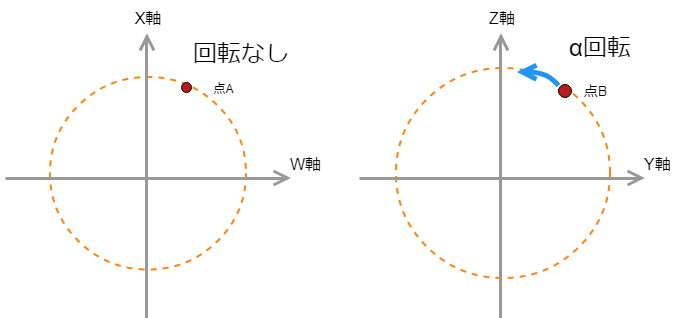
平面Aでの回転がα、平面Bでの回転が0(もしくは平面Aでの回転を0、平面Bでの回転をα)の場合の回転をSimple Rotationという。つまりどちらかの平面の回転角が0の場合だ。
simple rotationを実際にゲームでの回転操作で使うことはないと思われる。しかし四次元回転がどういう回転なのか一番理解しやすいのはこのsimple rotationだろう。なのでまずはこのsimple Rotationを理解することが大事だ。
Simple Rotationについて詳しい説明はここで ➡ 四次元回転の種類 Simple Rotation
Isoclinic Rotation
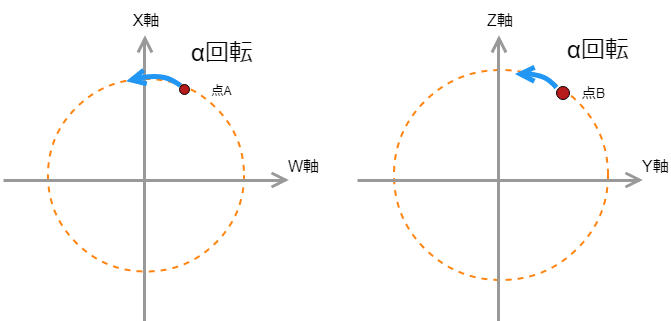
平面Aでの回転がα、平面Bでの回転が±αの場合の回転をIsoclinic Rotationという。つまり両方の平面で同じ大きさの回転角を持っている場合だ。(正負は逆でもいい)
Isoclinic Rotationは、クォータニオンによる回転の計算をする際には最も重要な回転だ。実際のクォータニオンによる回転の計算を構築するにはこのIsoclinic Rotationを使って式を構築する。もちろん、ゲームで回転を扱うときもこれを使って回転を計算する。この回転をマスターすれば、とりあえずはゲームで扱うようなクォータニオンによる回転は問題なく扱えるはずだ。
Isoclinic Rotationについて詳しい説明はここで ➡ 四次元回転の種類 Isoclinic Rotation
Double Rotation
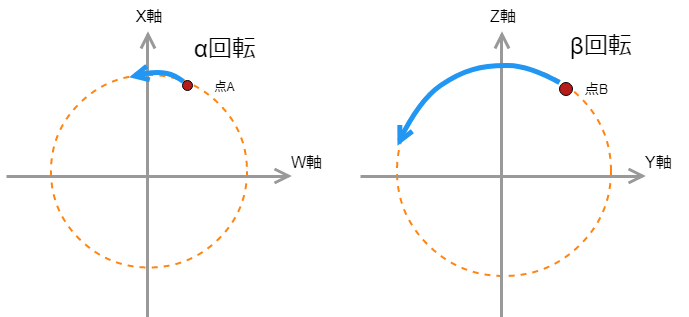
平面Aでの回転がα、平面Bでの回転がβの場合の回転をDouble Rotationという。どちらの平面でも別々の大きさの回転角を持っている場合の回転だ。
Double Rotationは両方の平面が回転してしまうので3次元空間上での回転のみにおさまっていない。それゆえ3次元空間での回転を扱うゲームで実際に使うことはないかもしれないが、Simple RotationとIsoclinic Rotationが特殊な状況での回転だったのと比較して、Double Rotationは一般化された4次元回転を表している。
Double Rotationについて詳しい説明はここで ➡ 四次元回転の種類 Double Rotation
参考
wikipedia 複素数、数平面、複素平面
https://ja.wikipedia.org/wiki/複素平面
wikipedia 四次元空間の回転
https://ja.wikipedia.org/wiki/回転_(数学)#四次元
クォータニオン考察 複素数
http://www.f-sp.com/entry/2017/06/30/221124
一般化されたクォータニオンの回転考察
https://qiita.com/HMMNRST/items/0a4ab86ed053c770ff6a
軸周りの回転、ちょっとわからなかった
https://mathtrain.jp/quaternion
GDCスライド
https://www.essentialmath.com/GDC2013/GDC13_quaternions_final.pdf