simple rotationを実際にゲームでの回転操作で使うことはないが、クォータニオンでの回転がどういうもかを一番感覚的につかみやすい。
四次元回転の種類 Simple Rotationとは
Simple rotationとは
平面Aでの回転がα、平面Bでの回転が0(もしくは平面Aでの回転を0、平面Bでの回転をα)の場合の回転をSimple Rotationという。つまりどちらかの平面の回転角が0の場合だ。
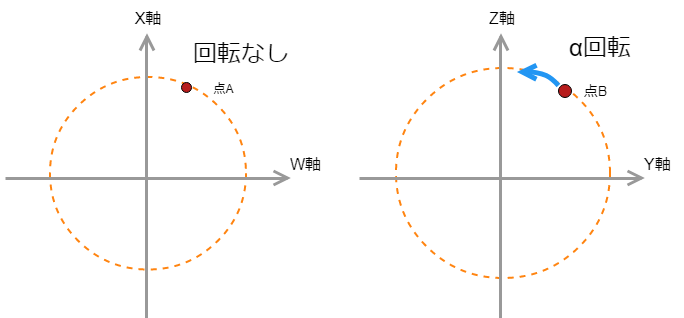
左の平面での回転は0で、右の平面ではα回転しているSimpleRotationの図 左の平面は固定されていると言う
平面の回転が0である状態を平面が固定されているという。ちなみに固定される平面の組み合わせは自由で、WY平面とXZ平面とかでもいい。
Simple rotationの特徴
平面での回転が0、すなわち固定されているということはどういうことか?回転が0ということは、その平面上で点の座標の変化がないということ。つまりこの回転角が0の平面での回転は合成後の回転に影響を与えないということ。逆に、もう一つの回転のある平面のみが全体の回転に影響を与えるということだ。
とはいっても、そう言われただけではまだどんな回転なのか見えてこないかもしれない。そこで実際に片方の平面を固定して、もう片方の平面を回転させる例を考えてみよう。
WX平面が固定の場合のSimpleRotationを考えてみる
具体的な例として、W軸とX軸が作るWX平面での回転角の大きさが0の場合を考えてみよう。
回転対象の点(w, x, y, z)をクォータニオンqで表した式は以下とする。
q = w + ix + jy + kz
まずWX平面を固定する
W軸とX軸が作る平面上での回転角が0である時、w軸とx軸が作るwx平面上での回転はないから、この平面上での点の位置は固定されている。
回転対象の点の座標が(w,x) = (1,2)だとしよう。この平面上で回転角が0だということは移動しないから(w,x) = (1,2)のままだということだ。wも1のままだし、xも2のまま。w軸は三次元空間上に存在しないが、 wのとる値の大きさは変わらないし、x軸は三次元空間上に存在しX軸上の点の値の大きさも変わらない。
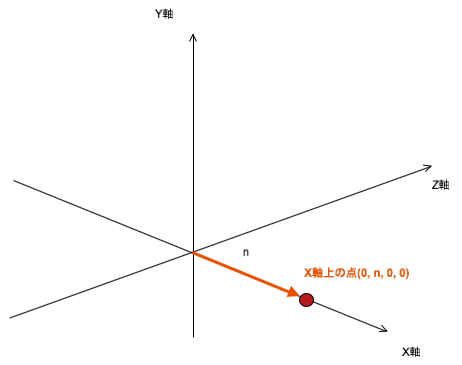
(w,x) = (1,1) 回転α = 0、つまりWX平面が固定されている時の様子。X軸上にあるこの点は動かない。
この状態がまさにwx平面が固定されている状態である。
三次元空間的に言えば、x軸上の点の位置が固定されているということだ。
次にYZ平面を回転させる
では次に残りの平面、つまりYZ平面での回転をみてみよう。WX平面は三次元空間上に存在しなかったが、YZ平面は三次元空間上にちゃんと存在する。YZ平面は三次元空間上のy軸とz軸に平行な平面だ。この平面がx軸上のどこにあるかというと、xの位置はWX平面によって固定されているから(x=nだとして)、図のようにあるx軸上の点(0, n, 0, 0)にYZ平面が存在する。
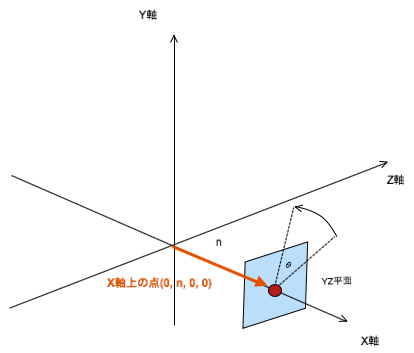
WX平面が固定されている時、残りのYZ平面の回転の様子を表した図
このYZ平面上での回転は基礎編で説明したような、複素数の乗算による回転で表現できる。
(\cos\theta + i\sin\theta) (x + iy) = x' + iy’
本来であればWX平面での回転とYZ平面での回転の合成がクォータニオンでの回転となるが、WX平面の回転はないのでSimple rotationにおいては、このYZ平面上での回転がそのままクォータニオンによる回転となる。
こうしてみると、SimpleRotationでは、X軸周りの三次元回転が表現できているようだ。
【ポイント】
ここで大事なのはWX平面が固定されたことで、X軸上の点の位置が固定されたと言うことだ。WX平面で回転が0でない場合、X軸上の点は移動してしまう。この状態ではX軸周りの回転をしようと思っても同時にX軸方向に移動が発生してしまう。そうすると、例えばゲームの中でゲームオブジェクトをX軸周りに回転させたいとなってもX軸方向への移動まで混じってしまうことになる。これは望ましい回転ではない。
クォータニオンの式ではこの回転をどう表す?
確かにsimple rotationは三次元空間における回転を表すことができることがわかった。しかしこれを最終的に求めたいクォータニオンの式
(a + bi + cj + dk) (w + ix + jy+ kz)
の形ではどのように表せるのか?
実はこの回転、クォータニオンの式では簡単には表現できない。その理由はクォータニオンのisoclinic rotationで説明するが、実際にクォータニオンの式で考える場合、一般的にはisoclinic rotationによる回転が一番扱いやすいことで知られている。
しかし概念的にはこのSimple Rotationは大事で、Isoclinic Rotationを使った回転でも最終的に片方の平面を固定(回転を0にする)ことで、もう片方の平面から三次元空間における回転を取り出す。これはまさに今やったことと同じだ。
回転行列でもSimple Rotationを表すことができる
このsimple rotationは回転行列を使って表すことができる。この式は今回の回転の例と同じで、WX平面の回転角が0でYZ平面がθ回転する場合の行列変換だ。
\begin{align}
\begin{pmatrix}
w' \\
x' \\
y' \\
z'
\end{pmatrix}
&=
\begin{pmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & \cos\theta & - \sin\theta \\
0 & 0 & \sin\theta & \cos\theta
\end{pmatrix}
\begin{pmatrix}
w \\
x \\
y \\
z
\end{pmatrix}\\
&=
\begin{pmatrix}
w \\
x \\
y\cos\theta - z\sin\theta \\
y\sin\theta + z\cos\theta
\end{pmatrix}
\end{align}
行列変換によるwxyzそれぞれの変化は
\begin{align}
w' &= w \\
x' &= x \\
y' &= y\cos\theta - z\sin\theta \\
z' &= y\sin\theta + z\sin\theta \\
\end{align}
w,xは全く同じ値で、y,zは基礎編で説明した複素数による回転と全く同じ変換になっているのがわかる。これはSimple Rotationでの想定通りの結果だ。このように行列で表すとsimple rotationがどのような回転なのか想像しやすい。
まとめ
simple rotationを考えることで四次元回転がどうやって三次元に適用されているのかがわかった。
まとめると、2つある平面のうち、W軸を含む平面を固定することで、三次元空間に存在するもう片方の平面での回転のみの回転が考えられるようになるということだ。
他の次元における回転と比較すると四次元回転は
・二次元回転は固定点を中心とした回転(原点を中心にθ回転)
・三次元回転は固定軸を中心とした回転(x軸を中心にα回転、y軸を中心にβ回転、z軸を中心にγ回転)
・四次元回転は、固定面を中心とする回転
を表現していることがわかる。
次は Isoclinic Rotation
SimpleRotationでは実際のクォータニオンの式を考えることができなかったが、それができるようになるのが
Isoclinic Rotationという種類の回転だ。この回転がわかればクォータニオンで回転の式を構築でき、ようやくゲーム内で回転操作を実践することができる。
Isoclinic Rotationはこちら ➡︎ クォータニオン 四次元回転の種類 Isoclinic Rotation
余談 Simple Rotationを解釈するにあたって迷ったこと
実は参考文献ではこのように説明されていた。
軸(1, 0, 0, 0)と(0, nx, ny, nx)が作る面が固定されていると解釈できる
最初はこの言葉が理解できなかった。
ん?辻褄が合わないな。。。W軸とX軸で作る平面の回転を固定したいのに。軸(1, 0, 0, 0)と(0, nx, ny, nx)ってなんのことを言っているんだ?と思った。
軸(1, 0, 0, 0)はわかるW軸を表現するならば(1, 0, 0, 0)だ、逆にX軸を表現するなら(0, 1, 0, 0)ということだ
でも(0, nx, ny, nx)は意味がわからなかった、全部の軸に値が存在するじゃないか。
w軸x軸y軸z軸の代わりに任意の軸(0, nx, ny, nz)を使っていいのか?
問題ないと思う。X軸上の点は(0, n, 0, 0)で表すことができて、x軸上の位置nを表している。
ではxyz空間に沿うものじゃないけど、任意の軸(0, nx, ny, nx)上の点も一つのパラメーター(0, n, 0, 0)で表すことができるはずだ。
でもこれ、任意の軸N(0, nx, ny, nx)を設定するときにパラメーターが3つも必要じゃん...
WX平面上の点が(w, x) = (1, 2)みたいに表せるように、2つの値で点の位置は決定されなければいけない。
しかしこれじゃ(w, N) = (1, ?)となってしまうではないか。
X軸(0, 1, 0, 0) ⇄ 任意の軸N(0, nx, ny, nx)
というようにX軸を任意の軸と置き換えられるような関係が必要だ。
ここで考えられる手法が2つある
・任意の軸N(0, nx, ny, nx)を基準とした新たな空間を作ってしまう考え方
・任意の軸N(0, nx, ny, nx)をX軸周りの回転、Y軸周りの回転、Z軸周りの回転に分解してから合成する考え方
◆ その1 任意の軸N(0, nx, ny, nx)を基準とした新たな空間を作ってしまう考え方
任意の軸(0, nx, ny, nx)を基準としたもう一つの空間を作ってしまうのはどうだろうか。この考え方はゲームワールドでワールド空間からローカル空間を階層的に作るような考え方に似ている。
任意の軸(0, nx, ny, nx)を別空間のX軸と捉える
任意の軸(0, nx, ny, nx)を作った後、その軸を基準に新たな空間を作り任意の軸(0, nx, ny, nx)は空間上のX軸と想定してしまう。するとnx, ny, nxは空間での姿勢を決めるためのベクトルと言えることができる。そうするとW軸(1, 0, 0, 0)とX軸(0, 1, 0, 0)の平面で考えていたように、W軸(1, 0, 0, 0)と任意の軸(0, nx, ny, nx)の平面を考えることができるようになる。
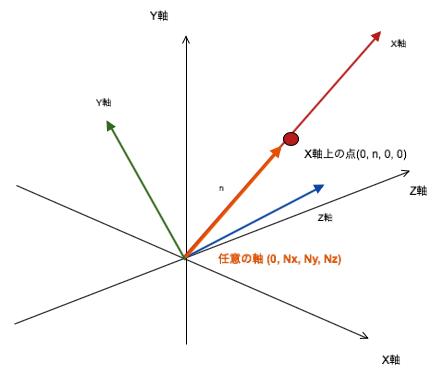
任意の軸(0, Nx, Ny, Nz)を新たな空間のX軸に対応させた様子
これによって軸(0, Nx, Ny, Nz)をX軸(0, n, 0, 0)で表現できるようになる
W軸と任意の軸N軸(0, Nx, Ny, Nz)を作る平面を固定する
SimpleRotationでは片方の平面を固定するのでWN平面を固定しよう。クォータニオンとは?で説明したように、回転がないということはWN平面上の回転は最終的な回転に影響を与えない。全ての回転はもう片方のYZ平面での回転βにのみ依存する。
この空間におけるYZ平面はどこにあるのだろうか?任意の軸N方向をX軸と捉えたということは、YZ平面は任意の軸(0, nx, ny, nx)に垂直に位置するはずである。YZ平面での回転は基礎編で説明したように、簡単な複素数同士の乗算で表すことができる。
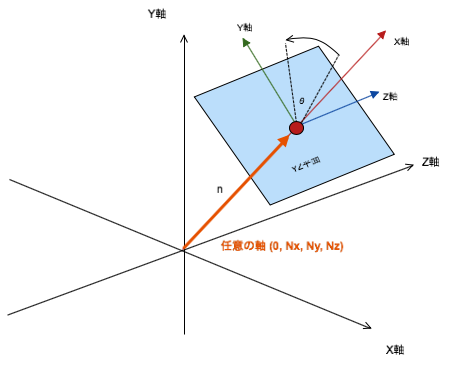
WX平面は固定されているから、もう片方のYZ平面の回転のみに依存している様子
YZ平面での回転はまさに、三次元空間における任意の軸周りの回転を表現している。
確かに任意の回転が表現できるかもしれないが式は?
任意の軸周りの回転を表現できることはわかったがこれをどうしたらクォータニオン同士の乗算
(a + bi + cj + dk) (w + ix + jy+ kz)
で表すことができるだろうか。これを考えるためには新しく考えた空間が、元の空間からどう回転しているかを考える必要がある。しかしであればX軸周りに回転させてから、さらに原点周りに回転移動させるのと何も違わない。後でわかったことだがこういった問題を解決するのがIsoclinic Rotationだ。
◆ その2 任意の軸NをX軸周りの回転、Y軸周りの回転、Z軸周りの回転に分解する考え方
今度は任意の軸のベクトルの成分を分解してそれぞれのxyz方向の回転の合成として考えてみよう。
任意の軸Nをベクトルをであると考え、この軸周りにθ回転する場合を考える
任意の軸Nは
N = (nx, ny, nz)
と表現できる。じゃあNを分解したX方向のベクトルnx周りの軸の回転だけを見てみる
Nを分解したX方向のベクトルnxは
nx = (0, nx, 0, 0)
このベクトル周りにをクォターニオンで表すと…
というように、どこかでクォータニオンの計算する必要が出てくる。SimpleRotationの知識だけではSimpleRotationも説明することができない。
参考
複素数、数平面、複素平面
https://ja.wikipedia.org/wiki/複素平面
回転
https://ja.wikipedia.org/wiki/回転_(数学)#四次元
クォータニオン考察 複素数
http://www.f-sp.com/entry/2017/06/30/221124
一般化されたクォターニオンの回転考察
https://qiita.com/HMMNRST/items/0a4ab86ed053c770ff6a
軸周りの回転、ほぼ考察なし
https://mathtrain.jp/quaternion
スライド
https://www.essentialmath.com/GDC2013/GDC13_quaternions_final.pdf