ゲーム開発で使うクォータニオンとはなんだろう?
クォータニオンはゲームオブジェクトなどの回転に使うということはわかっているが本当の意味では理解できていなかった。しかし実際に使うためにはクォータニオンがどういうものなのか理解していなければうまくは使えないだろう。そこで、何もわからない状態からクォータニオンの理解を深めていこうと思う。
複素数について
クォータニオンは複素数を知らないと理解できない。学校の数学でやったことがあると思うかもしれないけど基本的なことを復習してみよう。複素数は、このように表せる。
a + ib
aは実部といって、bは虚部という、これはどっちも実数だ。
iは虚数単位といって2乗すると-1になる。
i^2 = 1
例えば複素数 a + i b という
複素数 3 + i*7 \\
複素数 2 - i*3
複素平面について
ここから先は学校の数学ではやってないかもしれない。しかしこの複素平面を知らないでクォータニオンを理解することはできないだろう。
複素平面とは
複素数 a + ib で、この a と b は独立した実数だから、平面の直交座標(x, y)に対応させることができるのではないか?と考える
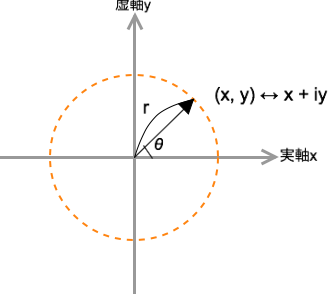
x+iyを平面に対応させた複素平面を表す図
実は数学的には、複素数 x + iy を平面の直交座標(x, y) に対応させたこの平面を複素平面(数平面)(ガウス平面)という。
なんでこんな平面を考える必要があったのだろうか?
結論から言うと、実部xと虚部yを、座標変面上で幾何学的に表すことができるからだ。
複素数に何か計算をしたとすると、その計算によって実部xと虚部yがどのように移動したか?この計算の意味を幾何学的に考えることができるのだ。
幾何学的な移動と捉える
例えば、複素数(1 + i3) というがあったとして、これがある計算によって複素数(5 + i9) になったとする
実部に注目すると 1 → 5、虚部に注目すると3 → 9となったということがわかる。
もし複素数に関する平面(x,y)を考えた場合、(1,3) → (5,9)に移動したと考えることができるようになる
複素平面を考えることで、この変化に対して幾何学的な意味を付加できるのだ。
意味の違う複素平面上での出来事が、実際の平面上に適用できるのか?と思うかもしれない。しかし結果的にみてしまえば、重要なのは移動による座標の変化のみでありそれがどのように変化したかは、実際の直交座標平面上でも複素平面上でも同じことだ。
複素平面でも普通の平面でも、実行する計算は同じ
だから「複素平面上である計算をすると(1,3) → (5,9)に移動した」とする場合、その計算が直交座標における計算に関係ないとしても「直交座標平面上の(1,3)に同じ計算をすると、(1,3)→(5,9)に移動した」ということが出来る。なぜなら実行する計算は同じだからだ。
このように複素平面上で計算した結果だけを利用しているに過ぎない。
簡単な例を考える
簡単な例を考えてみよう。
複素数(1 + i3)のxを+1すると複素数(2 + i3)になる。そうすると複素平面上ではx+1方向に平行移動したことになる、(1,3) → (2,3)になったということだ。これは直交座標平面上でx+1をして(1,3) → (2,3)になったということと全く同じことである。
実際のゲームでは
実際のゲームでは、回転に回転行列を使えば、実際の空間での移動を意味を考えて使うことができるけどこのクォータニオンは、実際の空間と全く関係がないから空間的な意味を考えて使うことはできない…
(x, y)を複素平面上に対応付けした結果、その複素平面上での回転が表現できることがわかったから
その計算だけを使おう!という話だ。
複素平面で極座標を考える
複素平面を考えることで、複素平面上で極座標を考えることができるようになった。
複素数(x + iy)の(x,y)座標を、原点から点(x, y)までの距離をr, 角度をθとして、極座標として考えてみると
x = r\cos\theta \\
y = r\sin\theta
つまり極座標で(x,y)を表すと
(x, y) → x + iy = r\cos\theta + i r\sin\theta = r\,(\cos\theta + i \sin\theta)
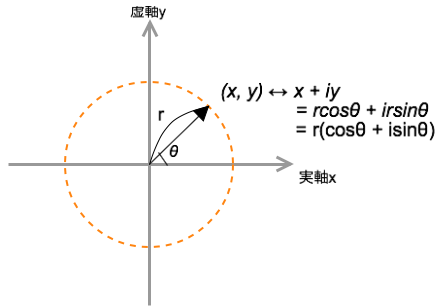
複素平面上の複素数(x,y)↔︎x + iyを、極座標で表している図
これは極座標を使った複素数のもう一つの表し方で、極形式という名前がある
複素数同士の掛け算が回転を表わす
実は複素数同士の掛け算は回転を表現していることがわかっている
実際に計算して確かめてみよう
二つの複素数を用意
いきなりだけど、半径r、角度αの複素数Aと、半径r、角度βの複素数Bの、二つの複素数を考えてみる
複素数A (r, \alpha) = r\,(\cos\alpha + i \sin\alpha) \\
複素数B (r, \beta) = r\,(\cos\beta + i \sin\beta)
よくわからないが極形式の複素数同士をかけてみる
この二つを積を計算してみると(積を計算する意味はわからないけど、三角関数の特性が何かしら使えるだろうと言う予測だと思う)
\begin{align}
r (\cos\alpha + i\,\sin\alpha)r (\cos\beta + i\,\sin\beta) &= r^2 (\cos\alpha\cos\beta + i\,\cos\alpha\sin\beta + i\,\sin\alpha\cos\beta + i^2\,\sin\alpha\sin\beta ) \\
&= r^2\,(\cos\alpha\cos\beta + i\,\cos\alpha\sin\beta + i\,\sin\alpha\cos\beta - \sin\alpha\sin\beta ) \\
&= r^2\,(\cos\alpha\cos\beta - \sin\alpha\sin\beta+ i\,(\cos\alpha\sin\beta + \sin\alpha\cos\beta) ) ← 加法定理!\\
&= r^2\,(\cos (\alpha+\beta) + i\,\sin (\alpha+\beta))\\
\end{align}
※加法定理
\cos (\alpha+\beta) = \cos\alpha\cos\beta - \sin\alpha\sin\beta \\
\sin (\alpha+\beta) = \cos\alpha\sin\beta + \sin\alpha\cos\beta
r = 1であるとすると(つまり半径r = 1の円)を考えた場合
\begin{align}
(\cos\alpha + i \sin\alpha)\,(\cos\beta + i \sin\beta) &= \cos (\alpha+\beta) + i\sin (\alpha+\beta) \\
複素数A (1, \alpha)*複素数B (1, \beta) &= 複素数C\,(1, \alpha+\beta)
\end{align}
極形式の複素数同士複素数A(1,α)と複素数B(1,β)をかけると新たな複素数C(1,α+β)になっている!
複素数C(1,α+β)はかけた二つの複素数の角度の和を持った複素数だ
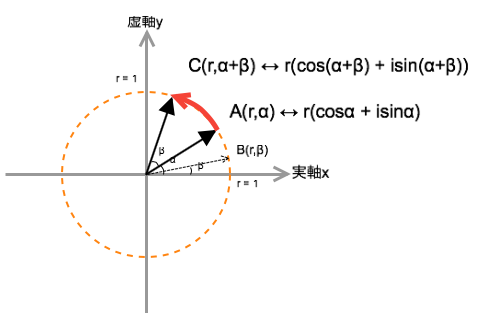
複素数A(r, α)に複素数B(r, β)をかけると、角度βだけ回転する様子を表した図
こうして見てみると、この計算によるの移動は、半径1の円周上の角度αにある点を角度βだけ足して回転移動させたというように捉えることができる。
実は理由があって複素数の極形式の複素数同士をかけていた!
最初はなぜ極形式の複素数同士をいきなりかけるのか、わからなかった。しかし乗算をしたのは理由がちゃんとあったみたいだった。それは乗算において複素数と行列が対応関係にあるということだ。だから回転行列は
\begin{align}
\begin{pmatrix}
x' \\
y'
\end{pmatrix}
&=
\begin{pmatrix}
\cos\theta & - \sin\theta \\
\sin\theta & \sin\theta \\
\end{pmatrix}
\begin{pmatrix}
x \\
y
\end{pmatrix}\\
\end{align}
であることがわかっているから、これをもとに複素数の乗算の式を構築することができたわけだ。
詳しくはこちら ➡ 10.1.7 クォータニオン 複素数と行列の関係の話
結論としては
複素数A (1, α)を原点周りにθ移動させたければ、複素数B (1, β)をかければいい
結論としては、複素数A(1, α)からみた場合、複素数A(1, α)に複素数B (1, β) をかけると、複素数C(1, α+β)になる。これは回転移動を表しているということができる
複素数A (1, \alpha)*複素数B (1, \beta) = 複素数C\,(1, \alpha+\beta)
ただし条件がある...
ただし極形式の複素数同士をかけた時にr =1としたことを思い出してほしい。
r=1でない場合これは成立しない。すなわち複素数(x + iy)でxの2乗とyの2乗の和は1でなければいけない。
x^2 + y^2 = 1
直交座標で回転を表してみよう
複素数同士の掛け算をすると、回転を表すことができることがわかった。でもそれが分かっただけでは実用的ではない。ゲームで使うには、平面上の座標(x,y)を回転させることを実際に考えてみなくてはいけない。
極形式の複素数を直交座標形式に変えてみる
前回わかったのは「複素数A (1, α)を原点周りにθ移動させたければ、複素数B (1, β)をかける」ということ
ここで極形式だろうと直交座標形式だろうと同じものを表していることを利用する。極形式と直交座標形式の関係はこのような式だ。
複素数A (1, \alpha) = r (\cos\theta + i \sin\theta) = 複素数A(x + iy)
するとこういう風に言い換えることができる。
極形式同士をかける場合「複素数A (1, α)を原点周りにθ移動させたければ、複素数B (1, β)をかける」
この式は
複素数A (1, \alpha) * 複素数B (1, \beta) = 複素数C (1, \alpha+\beta)
これを極形式で表された複素数A (1, α)を極形式で表して複素数A(x + iy)に置き換え、回転後の複素数Cも極形式で複素数C(x' + iy’)と置き換えると「複素数A(x + iy)を原点周りにθ回転させて複素数C(x' + iy’)に移動させたい場合、複素数B (1, β)をかける」
この式は
複素数A(x + iy) * 複素数B (1, \theta) = 複素数C(x' + iy')
実際の式で表してみる
これを式で表すと
(\cosθ + i \sinθ) (x + iy) = x' + iy'
左辺を計算すると
\begin{align}
(\cos\theta + i \sin\theta) (x + iy) &= x\cos\theta + ix\sin\theta + iy\cos\theta + i^2y\sin\theta (i^2 = -1) \\ &= x\cos\theta + ix\sin\theta + iy\cos\theta - y\sin\theta \\ &= (x\cos\theta - y\sin\theta) + i\,(x\sin\theta + y\cos\theta) \\
\end{align}
実部と虚部を比較すると、回転後のx’, y’はそれぞれ
x’ = x\cos\theta - y\sin\theta \\
y’ = x\cos\theta + y\sin\theta
なんと(x,y)を原点周りにθ回転させた(x’, y’)の座標がθだけで表現できている!
つまり直交座標における回転が表現できているということだ。
結論としては
結論としては、複素数平面を利用することで、平面上の座標(x,y)を原点周りにθ回転させた座標(x’, y’)はこのように表せる
x’ = x\cos\theta - y\sin\theta \\
y’ = x\cos\theta + y\sin\theta
この計算結果を使って、回転行列同様に回転を表すことができる。
r = 1の制限について
ただし同様に、今まで全てr = 1として考えているから(x, y)はxの2乗とyの2乗の和は1でなければいけない。
x^2 + y^2 = 1
同じことを行列で表現する場合
実は今回やった複素数を使った回転は、回転行列を使って同じことができる。
2次元空間において、(x, y)にある点をθだけ回して(x’, y’)に移動させる回転行列は(※縦優先行列であることに注意)
\begin{align}
\begin{pmatrix}
x' \\
y'
\end{pmatrix}
&=
\begin{pmatrix}
\cos\theta & - \sin\theta \\
\sin\theta & \sin\theta \\
\end{pmatrix}
\begin{pmatrix}
x \\
y
\end{pmatrix}\\
&=
\begin{pmatrix}
x\cos\theta - y\sin\theta \\
x\sin\theta + y\sin\theta \\
\end{pmatrix}
\end{align}
詳しくはこちら (1.0.1 行列変換)
クォータニオンへの適用
クォータニオンは二次元の話だった複素数を、四次元に拡張したものだ。
しかし四次元といっても実は、今回の二次元の複素平面を合成しているに過ぎない。
だからこの複素平面における回転を理解することは、クォータニオンを理解するうえでは欠かせない!
参考
複素数、数平面、複素平面
https://ja.wikipedia.org/wiki/複素平面