ようやく本題であるクォータニオンについて考えることができる。基礎編ではクォータニオンで使っている基本的な概念である複素数の理解を深めた。今回はその概念を拡張して実際にゲームで使うクォータニオンについて理解を深めよう。
クォータニオンとは
基礎編で説明したように、複素数では複素平面を考えることで二次元の回転を表すことができた。しかしこのままでは三次元での回転を表すことができない。
三次元での回転を表現するにはどうすれば?
複素数 (x + iy) を平面の直交座標(x, y) に対応させて複素平面を考えることで回転を考えることができた。では直交座標(x, y, z)に対応させるためにはどうすればいいだろうか?まず考えることができるのが、複素数 (x + iy + ?)のように対応する次元数を増やすということだ。
それこそがクォータニオン(四元数)
実部と虚部の2つしか次元のなかった複素数を、実部と3つ虚部を持つように拡張したものこそがクォータニオン(四元数)だ。クォータニオンqの式は
q = w + ix + jy + kz
複素数と同じように、a, b, cは実部、i, j, kは虚部といって、ijkは以下を満たす(乗法という)
i^2 = j^2 = k^2 = -1 \\
ij = k,\:jk = i,\:ki = j \\
ji = -k,\:kj = -i,\:ik = -j \\
しかし三次元空間は3つのパラメーターしかないのになぜ4つのパラメーターを考えたのか?
なぜ三次元じゃなくて、四次元を考えるのか?
三次元での回転を考えるのだから四次元ではなく三次元でいいじゃん、と思うかもしれない。しかし計算の都合上出来ないのだ。実際に計算してみよう。基礎編でやった二次元の回転を思い出してみると、複素数同士の
\begin{align}
(\cos\theta + i \sin\theta) (x + iy) &= x\cos\theta + ix\sin\theta + iy\cos\theta + i^2y\sin\theta (i^2 = -1) \\ &= x\cos\theta + ix\sin\theta + iy\cos\theta - y\sin\theta \\ &= (x\cos\theta - y\sin\theta) + i (x\sin\theta + y\cos\theta) \\
\end{align}
では同じことを三次元に拡張して計算して見ると(乗法を使う)
\begin{align}
(x + iy + jz) (x + iy + jz) &= x^2 + ivy + jxz + ixy + i^2y^2 + ijyz + jxz + jiyz + j^2z^2 \\
&= x^2 + ivy + jxz + ixy - y^2 + kyz + jxz - kyz - z^2 \\
&= x^2 - y^2 - z^2 + ivy + ixy + jxz+ jxz + kyz- kyz \\
&= (x^2 - y^2 - z^2) + i (vy + xy) + j (xz+ xz) + k (yz- yz) \\
\end{align}
元のx + iy + jzは三次元だった、しかし計算した結果、kという次元が新たにできてしまい次元数が一致しない。次元数が一致しない場合、実部と虚部同士を比較することができず座標の変換として使うことができないわけだ。
そこで4つめの次元を加えることでなんと、都合よく計算の前後で次元数が一致するようになる。この計算はクォータニオン同士の掛け算が回転を表すのではないか?で実際に計算しよう。
四次元空間の特徴
四次元空間は実際には存在しないから、三次元空間のように直感的に考えることができない。そこで、クォータニオン による回転を考える際に必要な四次元空間の特徴を把握しよう。ここではクォータニオンqは以下の式とする
q = w + xi + yj + zk
互いに直交する4本の軸がある
普通に考えれば直交する4本の軸があるはずがない。しかし四次元空間においては存在する。
例えば二次元から考えてみよう。二次元であれば 直交する2本の軸がある。これはよく見かける軸Xと軸Yが直交している直交座標系を思い出してもらえると想像できるだろう。
一般的な二次元空間を表す図
三次元であれば直交する3本の軸が存在する。三次元空間をX軸が右方向、Y軸が上方向、Z軸が奥行き方向に対応し、それぞれの軸が直交しているのはゲームワールド空間など三次元空間を考える時に見たことはあるだろう。
一般的な三次元空間を表す図
四次元であれば直交する4本の軸が存在する。確かに、空間的には3つまでなら直交する軸を置くことができるが、直交する4本の軸をおくことが出来ない。そこで「直交する3本の軸+全ての軸に垂直なもう一つの軸が存在する」ということができる。全ての軸に垂直なもう一つの軸は三次元空間的に存在することはできない。
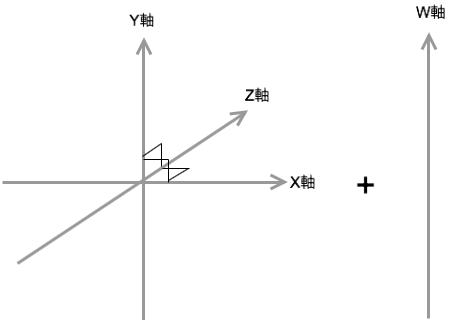
三次元空間と、空間上にはないがXYZ軸のどの軸とも直交するW軸の4つの軸で四次元空間が構成されるのを表した図
直交する2つの平面を考えることもできる
「互いに直行する4本の軸」があるということは、w軸とx軸は直行し、y軸とz軸も直行しているということ。ということは直交するw軸とx軸が作るwx平面, 直交するy軸とz軸が作るyz平面の2つの平面を考えることができる
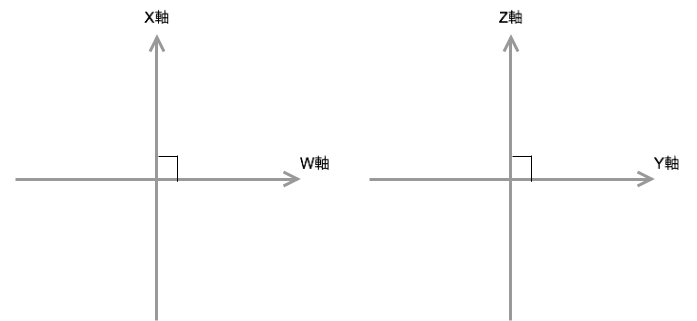
WX平面とYZ平面の2つの直交する平面を考えた図
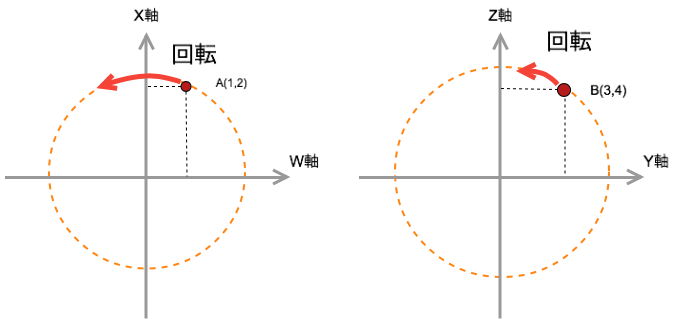
(w, x, y, z)を(w, x)と(y, z)に分けて考えることもできる
四次元空間上にある点を表すには
(w, x, y, z) = (1, 2, 3, 4)
とそれぞれ個別に表してもいいし、(w,y)と(y,z)のように別々に表してもいい
(w, x) = (1, 2) \\
(y, z) = (3, 4)
 `(w, x, y, z) = (1, 2, 3, 4)をWX平面とYZ平面の別々の平面で考えた図`
`(w, x, y, z) = (1, 2, 3, 4)をWX平面とYZ平面の別々の平面で考えた図`
このように四次元空間上の点を考えるときにはWX平面での位置と、YZ平面上での位置の合成として考えることができる。ちなみにWX平面、YZ平面上だけでなくどの組でもいい。
クォータニオンでの座標の移動
四次元空間の特性が分かったが最終的に考えるべきことは?
最終的には点A (x, y, z)を回転させてB(x’, y’, z’)に移動させることを考える。
複素数の場合を復習
複素数において回転を表した手順はこんな感じだった
①極座標形式で表す
②極座標で表した複素数同士を掛け算する
③なんとそれは回転を表していた!
クォータニオンは複素数の次元数を拡張しただけだからクォータニオンでも同じ理論で回転できるはずである。
クォータニオン同士の掛け算が回転を表すのではないか?
複素数と同じようにクォータニオン同士の掛け算が回転を表すのではないかと予想できる
ではクォータニオン同士を掛け算してみよう。
(a + bi + cj + dk) (e + fi + gj + hk) = (ae - bf - cg - dh) + (af + be + ch - dg)i + (ag - bh + ce + df)j + (ag + bg - cf + de)k
この結果を見ると次元数が同じである。であれば、実部と虚部同士を前後で比較でき
e’ = ae - bf - cg - dh \\
f’ = af + be + ch - dg \\
g’ = ag - bh + ce + df \\
h’ = ag + bg - cf + de \\
これはクォータニオン同士をかけると座標移動が表現できるということだ。しかし今の段階ではどんなクォータニオンをかければ回転移動を表現できるかはわからない...
回転移動も座標移動であり、何かしらのクォータニオン同士の乗算で回転移動を表現できるのではないかと予想できる。だから次に求めるべきはどんなクォータニオンが回転移動を表すのかだ。
どんなクォータニオンで回転移動を表現できる?
クォータニオン の乗算によって座標の移動ができる、ということはわかった。しかしどんなクォータニオンが回転を表すのか?
四次元空間の特徴でも話したように四次元空間は「2つの直交する平面から成り立っている」ということを思い出してみよう。基礎編で一つの平面での回転は複素数で表せることがわかった。ならば四次元における回転は、WX平面での回転とYZ平面での回転の合成として捉えられるのではないか?
二つの平面での回転の合成が四次元の回転になる
要素毎に分解する概念は別に四次元空間特有のものでなく、例えば三次元空間における任意のベクトルをx成分, y成分, z成分に分解できるのと同じようなもの。とはいえ、このように考えるだけではどんなクォータニオンが回転を表すクォータニオンなのかはわからないが、それを求める足がかりにはなりそうだ。
もちろん最終的には
(a + bi + cj + dk) (w + ix + jy+ kz)
といった形で回転を表すクォターニオンを求める必要がある。
このことの証明は次章で、実際にクォータニオン同士を計算することで証明していこうと思う。
続きはこちら ➡︎ 4次元回転の種類
参考
wikipedia 複素数、数平面、複素平面
https://ja.wikipedia.org/wiki/複素平面
wikipedia 四次元空間の回転
https://ja.wikipedia.org/wiki/回転_(数学)#四次元
クォータニオン考察 複素数
http://www.f-sp.com/entry/2017/06/30/221124
一般化されたクォータニオンの回転考察
https://qiita.com/HMMNRST/items/0a4ab86ed053c770ff6a
軸周りの回転、ちょっとわからなかった
https://mathtrain.jp/quaternion
GDCスライド
https://www.essentialmath.com/GDC2013/GDC13_quaternions_final.pdf