はじめに
実験データをFittingするとき、最小二乗法では、外れ値に引きずられて思ったような結果が得られない時があります。
精度評価指標と回帰モデルの評価にあるように、
最小二乗法は、実験データとFitting(回帰)との誤差(二乗平均平方根誤差(Root Mean Squared Error (RMSE))を最小化する方法です。この方法は、外れ値に対して弱い方法です。
外れ値に対して強い方法として、平均絶対誤差(Mean Absolute Error (MAE))を最小化する方法があります。これを行うには、scipy.optimize.fminを利用することでできます。
scipy.optimize.fmin
最適化問題(ある定義された関数の最小を解く問題)を解くモジュールとして、scipy.optimize.fminがあります。
Data fitting using fmin
Pythonで最適化問題入門
scipy.optimize.fmin
scipy.optimize.fminは、以下のパラメータを取ります。
fmin(func, x0, args=(), xtol=0.0001, ftol=0.0001, maxiter=None, maxfun=None,
full_output=0, disp=1, retall=0, callback=None, initial_simplex=None)
この関数を使うには以下のものが必要になります。
(1)func : callable func(x,*args)
The objective function to be minimized.
(2)x0 : ndarray
Initial guess.
(3)args : tuple, optional
Extra arguments passed to func, i.e. f(x,*args).
例題
平均絶対誤差で最小化の例題として、ある閾値から直線的に増加する関数を考えてみます。
pymc3でのモデル関数が条件分岐を含む場合の書き方
# Import
import numpy as np
from scipy.optimize import fmin
import scipy as sp
import matplotlib.pyplot as plt
%matplotlib inline
ある閾値(u)から一次関数で増加する関数を作ります。
# vectorizeしています。
@np.vectorize
def line(x, u, nor, bg):
ud = x - u
if ud <= 0:
f = bg
else:
f = nor*ud + bg
return f
グラフを書いてみます。
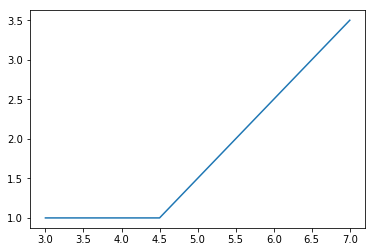
xx = np.arange(3, 7.1, 0.1)
y_data = line(xx,4.5,1.0,1.0)
plt.plot(xx,y_data)
plt.show()
4.5から直線的に増加します。(バックグランドが1、傾きが1)
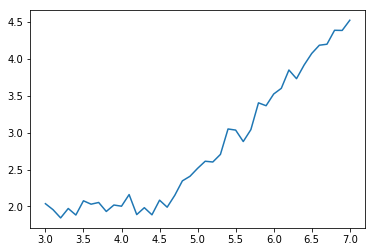
# このデータにガウスノイズを重畳します。
g_noise=np.random.normal(1, 0.1, len(xx))
yg = y_data+ g_noise
plt.plot(xx,yg)
plt.show()
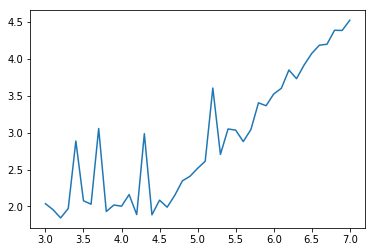
# 外れ値導入するためにポアソンノイズを重畳します。
p_noise=np.random.poisson(0.1, len(xx))
yp = y_data+g_noise+ p_noise
plt.plot(xx,yp)
plt.show()
ガウスノイズ重畳とガウスノイズとポアソンノイズ重畳したそれぞれを測定データとして、line関数で誤差関数としてRMSEとMAEそれぞれでFittingを行います。
fminで利用する関数を定義します。
# 測定と予測の差の残差を求めます。
def line_residual_func(parameter, x, y):
'''
line reidual function
'''
residual = y - line(x, parameter[0], parameter[1], parameter[2])
return residual
# 平均絶対誤差(mae)
def line_abs_residual_sum(parameter,x,y):
'''
mean absolute error (mae)
'''
line_abs_residual=np.abs(line_residual_func(parameter, x, y)).sum()
return line_abs_residual
# 二乗平均平方根誤差(rmse)
def line_sq_residual_sum(parameter, x, y):
'''
root mean square error (rmse)
'''
line_sq_residual = np.sqrt((np.abs(line_residual_func(parameter, x, y))*np.abs(line_residual_func(parameter, x, y))).sum())
return line_sq_residual
# fminによる最小化
def abs_line_fit(xdata,ydata,para):
fit_para = fmin(line_abs_residual_sum,para,args=(xdata,ydata))
fit_line =line(xdata,fit_para[0],fit_para[1],fit_para[2])
return fit_line, fit_para
def lsq_line_fit(xdata,ydata,para):
fit_para = fmin(line_sq_residual_sum,para,args=(xdata,ydata))
fit_line = line(xdata,fit_para[0],fit_para[1],fit_para[2])
return fit_line, fit_para
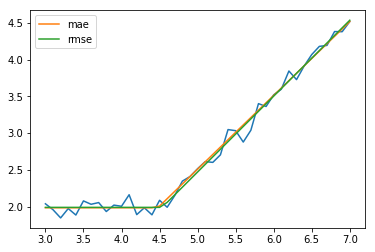
ガウスノイズを重畳したデータをmaeとrmseで最小化します(Fitting)。
ini_para = (4.5,1.0,1.0)
# mae
fit_g_abs,para_g_abs = abs_line_fit(xx,yg,ini_para)
# rmse
fit_g_lsq,para_g_lsq = lsq_line_fit(xx,yg,ini_para)
# Fittingの当てはまりを評価するためにR2(決定係数)を計算します。
from sklearn.metrics import r2_score
r2_g_abs = r2_score(yg, fit_g_abs)
r2_g_lsq = r2_score(yg, fit_g_lsq)
print('mae:',para_g_abs, 'R2:',r2_g_abs)
print('rmse:',para_g_lsq, 'R2:',r2_g_lsq)
plt.plot(xx,yg)
plt.plot(xx,fit_g_abs, label='mae')
plt.plot(xx,fit_g_lsq, label='rmse')
plt.legend()
plt.show()
Optimization terminated successfully.
Current function value: 2.719556
Iterations: 124
Function evaluations: 224
Optimization terminated successfully.
Current function value: 0.537687
Iterations: 96
Function evaluations: 173
mae: [4.47714667 1.00438872 1.98376745] R2: 0.9902022990260891
rmse: [4.53396446 1.03279902 1.98906734] R2: 0.9906241308439305
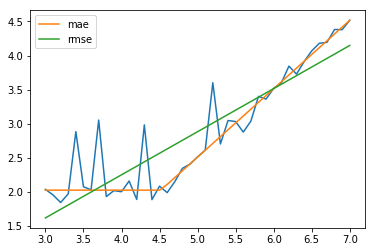
ガウスノイズ、ポアソンノイズを重畳したデータをmaeとrmseで最小化します(Fitting)。
ini_para = (4.5,1.0,1.0)
# mae
fit_p_abs,para_p_abs = abs_line_fit(xx,yp,ini_para)
# rmse
fit_p_lsq,para_p_lsq = lsq_line_fit(xx,yp,ini_para)
# Fittingの当てはまりを評価するためにR2を計算します。
# from sklearn.metrics import r2_score
r2_p_abs = r2_score(yg, fit_p_abs)
r2_p_lsq = r2_score(yg, fit_p_lsq)
print('mae:',para_p_abs, 'R2:',r2_p_abs)
print('rmse:',para_p_lsq, 'R2:',r2_p_lsq)
plt.plot(xx,yp)
plt.plot(xx,fit_p_abs,label='mae')
plt.plot(xx,fit_p_lsq,label='rmse')
plt.legend()
plt.show()
Optimization terminated successfully.
Current function value: 6.215268
Iterations: 176
Function evaluations: 310
Optimization terminated successfully.
Current function value: 2.504935
Iterations: 61
Function evaluations: 114
mae: [4.51719703 1.00317946 2.02706036] R2: 0.9892638820822436
rmse: [2.85243769 0.6320154 1.52663347] R2: 0.8702849912887191
今度は、rmseで最小化した方はうまくFittingできていないようです。