Pythonで最適化問題入門

背景

第三弾になりますが、タイトル通り入門編として記載します。

最適化問題とは

簡単に言うと、ある定義された関数の最小を導く問題です。

定義関数例

簡単な2次関数にします。

def f(x):
    return x**2

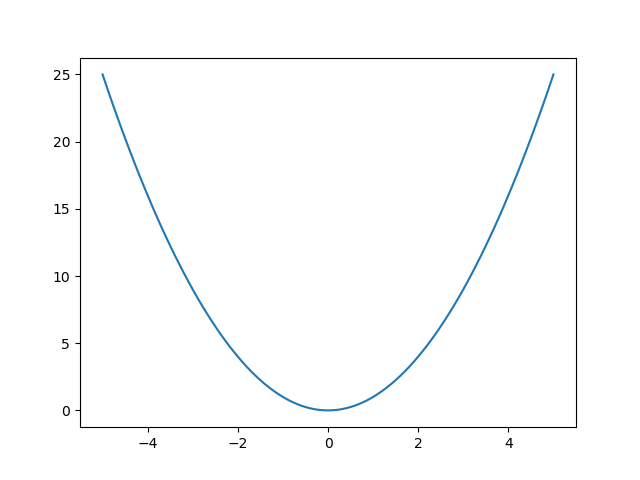
分かりやすく描画します。

import matplotlib.pyplot as plt
import numpy
x = numpy.arange(-5, 5.1, 0.1)
plt.plot(x, f(x))
plt.show()

はい、とってもシンプルな例です。

定義注意

最適化問題の関数はscipyに含まれています（事前にインストールしてください）

ここで一点注意、普通にimport定義すると怒られます。

import scipy
scipy.optimize

Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
AttributeError: 'module' object has no attribute 'optimize'

scipy.optimizeを使うには、公式サイトにも書いてありますが

from scipy import optimize

と定義しましょう。

最適化

一般的な滑降シンプレックス法、Nelder–Mead法で行います。
こちらはscipyではscipy.optimize.fmin関数が該当します。

この関数何だっけ？使い方どうするんだっけ？という場合はnumpy.infoで確認できます。

import numpy
from scipy import optimize
numpy.info(optimize.fmin)

 fmin(func, x0, args=(), xtol=0.0001, ftol=0.0001, maxiter=None, maxfun=None,
      full_output=0, disp=1, retall=0, callback=None, initial_simplex=None)

Minimize a function using the downhill simplex algorithm.

This algorithm only uses function values, not derivatives or second
derivatives.

Parameters
----------
func : callable func(x,*args)
    The objective function to be minimized.
x0 : ndarray
    Initial guess.
args : tuple, optional
    Extra arguments passed to func, i.e. ``f(x,*args)``.
xtol : float, optional
    Absolute error in xopt between iterations that is acceptable for
    convergence.
ftol : number, optional
    Absolute error in func(xopt) between iterations that is acceptable for
    convergence.
maxiter : int, optional
    Maximum number of iterations to perform.
maxfun : number, optional
    Maximum number of function evaluations to make.
full_output : bool, optional
    Set to True if fopt and warnflag outputs are desired.
disp : bool, optional
    Set to True to print convergence messages.
retall : bool, optional
    Set to True to return list of solutions at each iteration.
callback : callable, optional
    Called after each iteration, as callback(xk), where xk is the
    current parameter vector.
initial_simplex : array_like of shape (N + 1, N), optional
    Initial simplex. If given, overrides `x0`.
    ``initial_simplex[j,:]`` should contain the coordinates of
    the j-th vertex of the ``N+1`` vertices in the simplex, where
    ``N`` is the dimension.

Returns
-------
xopt : ndarray
    Parameter that minimizes function.
fopt : float
    Value of function at minimum: ``fopt = func(xopt)``.
iter : int
    Number of iterations performed.
funcalls : int
    Number of function calls made.
warnflag : int
    1 : Maximum number of function evaluations made.
    2 : Maximum number of iterations reached.
allvecs : list
    Solution at each iteration.

こんな形で引数や出力、この関数の意味など詳細が確認できます。

では最適化します。

optimize.fmin(f, 1)

Optimization terminated successfully.
         Current function value: 0.000000
         Iterations: 18
         Function evaluations: 36
array([-1.77635684e-15])

最小値は-1.77635684e-15と算出されました。
他の内容はその時の関数の値、最適化時のイテレーション回数や関数の回数等です。

補足

「ある範囲内」という場合はoptimize.fminboundという関数もあります。

optimize.fminbound(f, 2, 3, full_output=1)

(2.000005960860986, 4.000023843479476, 0, 25)

そもそもですが、一次関数程度ならoptimize.brentという関数も存在します。

optimize.brent(f, brack=(1,2), full_output=1)

(0.0, 0.0, 4, 5)

もっともっというと、optimize.minimizeという関数が存在します。

optimize.minimize(f, 1.0, method='Nelder-Mead')

final_simplex: (array([[-8.8817842e-16],
       [ 9.7656250e-05]]), array([7.88860905e-31, 9.53674316e-09]))
           fun: 7.888609052210118e-31
       message: 'Optimization terminated successfully.'
          nfev: 34
           nit: 17
        status: 0
       success: True
             x: array([-8.8817842e-16])

minimizeの公式ドキュメントを見ると、他にも様々な手法が可能です。

以上で最適化問題の入門編ということで終わりにします。