はじめまして、りょーつといいます。高専出身の大学院2年生です。研究の専門は力学や機構学で、Qiitaでは主に制御工学や数学に関する記事を書いています。研究室でデジタル信号処理が流行っていたので最近はそれ関連の記事を書いています。本稿が信号処理関連の最後の記事になる予定です。これまでの記事は以下のリンクからどうぞ。
デジタル信号処理① ラプラス変換とZ変換の関係性
デジタル信号処理② 双一次変換の必要性とイメージ
デジタル信号処理③ ローパスフィルタの実装方法
目次
1.はじめに
2.双一次変換と周波数応答
3.検証実験
4.おわりに
5.付録
1. はじめに
本稿では、前回の記事で紹介したデジタルローパスフィルタの周波数応答についてまとめてみようと思います。少しだけプリワーピングにも触れようと思います。ラプラス変換とZ変換の関係をしっかりおさえておくと、本記事の内容が理解しやすいです。
2. 双一次変換と周波数応答
これまでにラプラス変換の$s$とZ変換の$z$をつなぐ関係式として以下の2つを紹介しました。
s = \dfrac{2}{\Delta t} \dfrac{1 - z^{-1}}{1 + z^{-1}}
\tag{1}
z = e^{s'\Delta t}
\tag{2}
ただし、$\Delta t$はデータのサンプリング周期です。(1)式は双一次変換と呼ばれ、伝達関数を離散化するために使用されます。一方(2)式は離散化されたデータを無理やりラプラス変換したときに得られる関係式です。(2)式のラプラス演算子を$s$ではなく$s'$としているのは、離散データのラプラス変換はラプラス変換の定義
\mathcal{L} [ f(t)]= \int_{0}^{\infty} f(t) e^{-st} dt
\tag{3}
を厳密に満たしているわけではない(離散データは幅を持たないので厳密には積分結果が0になる)ためです。私は離散データのラプラス変換を「ラプラス変換もどき」と呼ぶことにしています。これらの関係を図1にまとめました。フワッと書くとラプラス変換してから離散化するか、そもそも離散的なものを無理やりラプラス変換しているかの違いがあります。

図1 ラプラス変換とラプラス変換もどき
伝達関数の周波数応答はラプラス演算子$s$に対して角周波数$\omega$を代入することで解析できます。しかし、ラプラス変換とラプラス変換もどきは別物なので、$s'$に対応する角周波数$\omega'$も考えます。それぞれの周波数解析を式で表すと以下のようになります。
s = j\ \omega
\tag{4}
s' = j\ \omega'
\tag{5}
これらの準備が整うと、ラプラス変換とラプラス変換もどきのズレを周波数応答の観点から可視化することができます。(1)(2)(4)(5)式から$z$、$s$、$s'$を消去して整理すると
\dfrac{1}{2} \omega \Delta t = \tan{\bigg(\dfrac{1}{2} \omega' \Delta t \bigg)}
\tag{6}
の関係が得られます。導出過程は付録にまとめました。(6)式は、デジタルフィルタの設計に使用する角周波数$\omega'$は実際の信号において(6)式で表されるような周波数$\omega$に変換されてしまうことを意味しています。つまり、デジタルフィルターのカットオフ角周波数$\omega'_c$を設定したとしても実際には(6)式のズレが生じるので補正しないといけないのです。このような補正をプリワーピングと言います。具体的にはデジタルフィルタの差分方程式の$\omega'_c$に(6)式の$\omega$を再度代入すればよいです。
ただし、サンプリング周期$\Delta t$が十分小さければそのような問題は起きません。(6)式の右辺を$\Delta t$についてマクローリン展開すると
\tan{\bigg(\dfrac{1}{2} \omega' \Delta t \bigg)}
=
\dfrac{1}{2}\omega'\Delta t + \dfrac{1}{24}{\omega'}^3 {\Delta t}^3 + \cdots
\tag{7}
であり、$\Delta t$の2次以上の項を無視すれば
\dfrac{1}{2} \omega \Delta t
\simeq
\dfrac{\omega'}{2}\Delta t
\therefore
\omega \simeq \omega'
\tag{8}
になるためです。これは直観的な結果だと思います。サンプリング周期が小さくてデータの欠損が少なければ、周波数応答が一致、サンプリング周期が大きくて、データの欠損が増加すれば、周波数応答がズレていくというイメージです。
サンプリング周期$\Delta t$の大きさによって応答が変わる様子は次章で確認したいと思います。
3. 検証実験
ここでは1次のローパスフィルタに周期入力信号$u(t)$を与えた場合の出力$y(t)$を考えます。ローパスフィルタの時定数を$T$、カットオフ角周波数を$\omega_c$としたとき、その伝達関数$G(s)$は
G(s) = \dfrac{1}{1 + Ts} = \dfrac{\omega_c}{\omega_c + s}
\tag{9}
で与えられます。入力信号$u(t)$をシンプルな三角関数
u(t) = \sin{\omega t}
\tag{10}
としたとき、ローパスフィルタの出力$y(t)$は
y(t) = \dfrac{\omega_c}{{\omega_c}^2 + \omega^2}
\bigg( \omega \Big( e^{-\omega_c t} - \cos{\omega t} \Big) +\omega_c \sin{\omega t} \bigg)
\tag{11}
となります。初期値は$y(0) = 0$としました。計算過程は付録に書いておきます。
このようなローパスフィルタをデジタルで実装する場合は前回の記事を参考に以下のような漸化式を使えばよいです。
y_n = y_{n-1} + \dfrac{\omega_c' \Delta t}{2 + \omega_c' \Delta t}
\Big( u_n + u_{n-1} - 2y_{n-1} \Big)
\tag{12}
y_0 = 0
\tag{13}
では$\omega = 20$とした場合に(11)式のアナログフィルタの出力と(12)式のデジタルフィルタの出力を比較してみましょう。まずはサンプリング周期$\Delta t$が入力信号$u(t)$の周期に対して十分小さい場合($\Delta t = 0.001$ [s])を考えます。カットオフ角周波数を$\omega_c = \omega'_c = 10\omega$とした場合の出力を図2に、$\omega_c = \omega'_c = \omega$とした場合の出力を図3に、$\omega_c = \omega'_c = 0.1\omega$とした場合の出力を図4にそれぞれ示しました。黒線の$y(t)$がアナログフィルタ、赤線の$y(n\Delta t)$がデジタルフィルタの出力を意味しています。
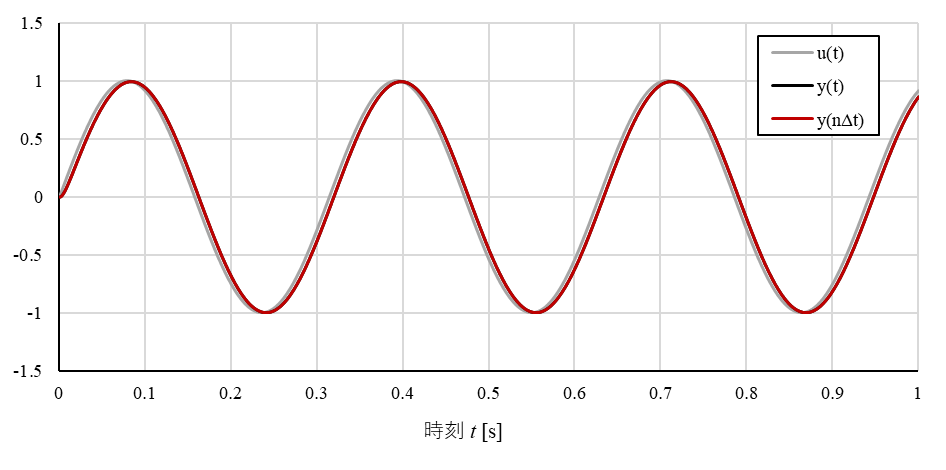
図2 $\omega_c = \omega'_c = 10\omega$の場合の出力
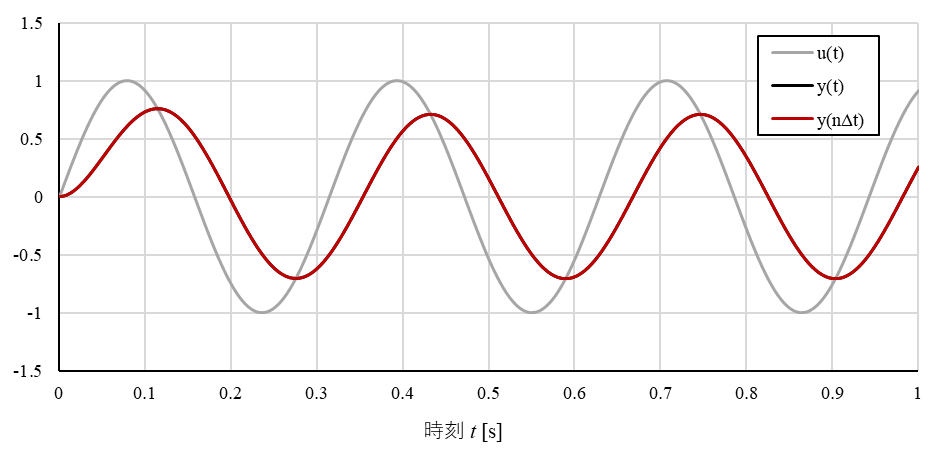
図3 $\omega_c = \omega'_c = \omega$の場合の出力

図4 $\omega_c = \omega'_c = 0.1\omega$の場合の出力
図2~図4の結果から、(8)式で示したとおり、$\Delta t$が十分小さい場合にアナログフィルタとデジタルフィルタの出力がほぼ一致していることが分かります。また、カットオフ周波数$\omega_c$、$\omega'_c$が小さくなるにつれて出力信号が減衰していくことが読み取れますね。
次にサンプリング周期$\Delta t$を大きくした場合を考えてみます。$\Delta t = 0.1$ [s]、$\omega_c = \omega'_c = \omega$とした場合の出力を図5に示しました。

図5 $\Delta t = 0.1$ [s]、$\omega_c = \omega'_c = \omega$の場合の出力
図3とは異なり、デジタルフィルタの出力がより大きく減衰していることが分かります。これは離散化の影響によりカットオフ周波数がズレてしまったことが原因です。そこで前章でしょうかプリワーピングを使ってみましょう。
(6)式に$\omega'_c = 20$を代入すると$\omega_c = 31.15$が得られます。つまり、実際には$\omega'_c = 20$ではなく$\omega'_c = 31.15$として設計しなければならなかったということが分かります。このような補正を施した場合の出力は図6のようになります。
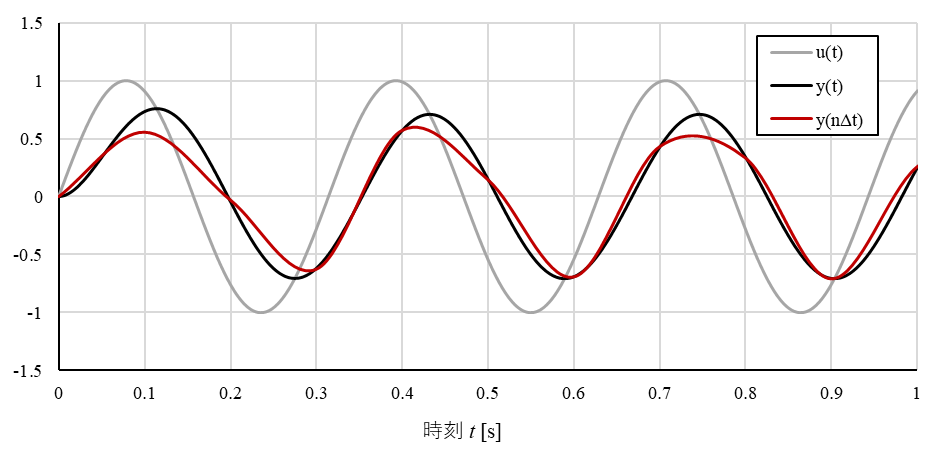
図6 $\Delta t = 0.1$ [s]、$\omega_c = 20$、$\omega'_c = 31.15$の場合の出力
図5と比較して減衰量や位相がアナログフィルタの出力に近くなっていることが分かりますね。このようにして補正するのがプリワーピングです(多分)。
4. おわりに
本稿ではデジタルローパスフィルタの周波数解析についてフワッとまとめました。サンプリング周期とかを考慮してしっかり実装したのは初めてだったのでとても楽しかったです。本記事でデジタル信号処理シリーズは完結とします。
さいごまで読んでいただきありがとうございました!
5. 付録
5.1 (6)式の導出過程
まず(2)式を(1)式に代入すると
s = \dfrac{2}{\Delta t} \dfrac{1 - e^{-s'\Delta t}}{1 + e^{-s'\Delta t}}
\tag{a}
が得られる。さらに(a)式へ(4)(5)式を代入し、以下のように変形する。
j\omega
=
\dfrac{2}{\Delta t} \dfrac{1 - e^{-j\omega'\Delta t}}{1 + e^{-j\omega'\Delta t}}
=
\dfrac{2}{\Delta t} \dfrac{e^{\frac{1}{2}j\omega'\Delta t} - e^{-\frac{1}{2}j\omega'\Delta t}}{e^{\frac{1}{2}j\omega'\Delta t} + e^{-\frac{1}{2}j\omega'\Delta t}}
\tag{b}
ここでオイラーの公式より
\cos{\Big(\frac{1}{2}\omega'\Delta t \Big)}
=
e^{\frac{1}{2}j\omega'\Delta t} + e^{-\frac{1}{2}j\omega'\Delta t}
\tag{c}
j \sin{\Big(\frac{1}{2}\omega'\Delta t \Big)}
=
e^{\frac{1}{2}j\omega'\Delta t} - e^{-\frac{1}{2}j\omega'\Delta t}
\tag{d}
であることを(b)式に代入し、整理することで(6)式が得られる。
j\omega
=
\dfrac{2}{\Delta t} \dfrac{j \sin{\Big(\frac{1}{2}\omega'\Delta t \Big)}}{\cos{\Big(\frac{1}{2}\omega'\Delta t \Big)}}
=
j \dfrac{2}{\Delta t} \tan{\Big(\frac{1}{2}\omega'\Delta t \Big)}
\therefore
\dfrac{1}{2} \omega \Delta t
=
\tan{\Big(\frac{1}{2}\omega'\Delta t \Big)}
\tag{e}
5.2 (11)式の導出過程
まずラプラス変換表を参考に(10)式の両辺をラプラス変換すると以下の式が得られる。
U(s)
=
\mathcal{L} [ u(t)]
=
\dfrac{\omega}{s^2 + \omega^2}
\tag{f}
$s$領域における出力$Y(s)$は(9)式の伝達関数と(f)式の入力をもとに
Y(s)
=
G(s)U(s)
=
\dfrac{\omega \ \omega_c}{(s^2 + \omega^2)(s + \omega_c)}
\tag{g}
となる。(g)式の分母を因数分解し、全体を部分分数分解すると以下の式が得られる。
Y(s)
=
\dfrac{\omega \ \omega_c}{{\omega_c}^2 + \omega^2}
\Bigg( \dfrac{1}{s + \omega_c} - \dfrac{s-\omega_c}{s^2 + \omega^2} \Bigg)
=
\dfrac{\omega \ \omega_c}{{\omega_c}^2 + \omega^2}
\Bigg( \dfrac{1}{s + \omega_c} - \dfrac{s}{s^2 + \omega^2}
+ \dfrac{\omega_c}{\omega} \dfrac{\omega}{s^2 + \omega^2} \Bigg)
=
\dfrac{ \ \omega_c}{{\omega_c}^2 + \omega^2}
\Bigg( \dfrac{\omega}{s + \omega_c} - \dfrac{\omega s}{s^2 + \omega^2}
+ \dfrac{\omega_c\ \omega}{s^2 + \omega^2} \Bigg)
\tag{h}
最後に(h)式を逆ラプラス変換することで(11)式が導出される。
y(t)
=
\mathcal{L}^{-1} [ Y(s)]
=
\dfrac{ \ \omega_c}{{\omega_c}^2 + \omega^2}
\Bigg( \omega e^{-\omega_c t} - \omega \cos{\omega t} + \omega_c \sin{\omega t} \Bigg)
\therefore
y(t) = \dfrac{\omega_c}{{\omega_c}^2 + \omega^2}
\bigg( \omega \Big( e^{-\omega_c t} - \cos{\omega t} \Big) +\omega_c \sin{\omega t} \bigg)
\tag{i}