デジタル信号処理① ラプラス変換とZ変換の関係性

　はじめまして、りょーつといいます。高専出身の大学院2年生です。研究の専門は力学や機構学で、Qiitaでは主に制御工学や数学に関する記事を書いています。最近研究室でデジタル信号処理が流行っているので今週はそれ関連の記事を書いてみました。

目次

1.はじめに
2.ラプラス変換の復習
3.ラプラス変換と片側Z変換の関係
4.Z変換のシフト操作
5.おわりに
6.参考文献
7.付録

1. はじめに

　本稿ではデジタル信号処理に登場する片側Z変換についてその図的イメージやラプラス変換との対応関係についてまとめようと思います。「ラプラス変換はある程度学んだことあるけどデジタル制御に手を出した瞬間分からなくなってしまった」みたいな感じの方へ刺さる内容になると思います。「Z変換はラプラス変換でいうアレ」という対応関係がイメージできるようになれる記事を目指します。大学の一般教養程度の数学の知識を必要とします。また、初期値とか複素数の扱いとかの厳密な部分はフワッと流すことにします。

2. ラプラス変換の復習

　本稿で使用するラプラス変換の知識について軽くおさらいしようと思います。まず、関数$f(t)$のラプラス変換は以下のように定義されます。

\mathcal{L} [ f(t)]= F(s) = \int_{0}^{\infty} f(t) e^{-st} dt
\tag{1}

ここで$s$はとある複素数です。一般的にラプラス変換の結果は大文字で表されることが多いようです。
　ラプラス変換は定積分の計算結果なので、図的にイメージするなら図1の塗りつぶされた部分の面積で表現できると考えられます。

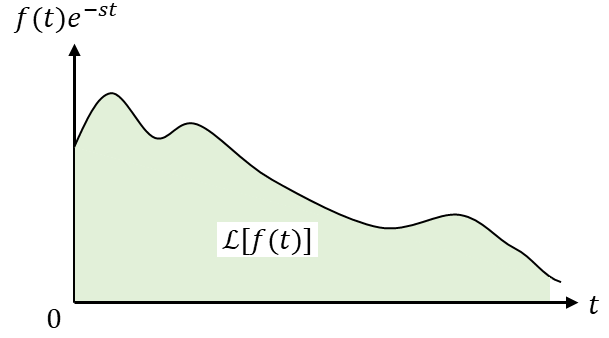
図1　ラプラス変換の図的イメージ

　また、むだ時間要素についても少し触れておきます。システムへの入力$u(t)$と出力$y(t)$の間$T$の遅れがある場合を考えます。

y(t) = u(t - T)
\tag{2}

なお$u(t)$は$0\le t < T$の範囲で$0$であると仮定します。
　(2)式の右辺を置換積分を駆使してラプラス変換すると

\mathcal{L} [ u(t - T)] 
=
\int_{0}^{\infty} u(t - T) e^{-st} dt

=
\int_{T}^{\infty} u(t - T) e^{-st} dt

=
\int_{0}^{\infty} u(\tau) e^{-s(\tau + T)} dt

=e^{-sT}\int_{0}^{\infty} u(\tau) e^{-s\tau} dt

\therefore
\mathcal{L} [ u(t - T)] 
=
U(s)e^{-sT}
\tag{3}

となります。(2)式の左辺もラプラス変換し、入出力関係を比較すると

Y(s)
=
U(s)e^{-sT}
\tag{4}

であり、$s$領域では信号の「ズレ」が$e^{-sT}$という指数関数で表現できることが分かります。

3. ラプラス変換と片側Z変換の関係

　ここから本題に入ります。まずは片側Z変換の定義を確認しましょう。ある点列$x_n$のZ変換は以下のように定義されます。

\mathcal{Z}[x_n]
=
X(z)
= \sum_{n = 0}^{\infty}  x_{n} z^{-n} 
\tag{5}

定義はさておき、(5)式のラプラス変換との関係性についてまとめたいと思います。一言でいうと、片側Z変換はラプラス変換の離散データバージョンとなります。丁寧に説明していきます。
　まずはある関数$f(t)$をサンプリング周期$T$でサンプリングして得られる点列$x_n$を用意します。式で書くと

x_0
=
f(0)

x_1
=
f(T)

x_2
=
f(2T)

\vdots

x_n
=
f(nT)
\tag{6}

となります。図的イメージは図2のようになります。

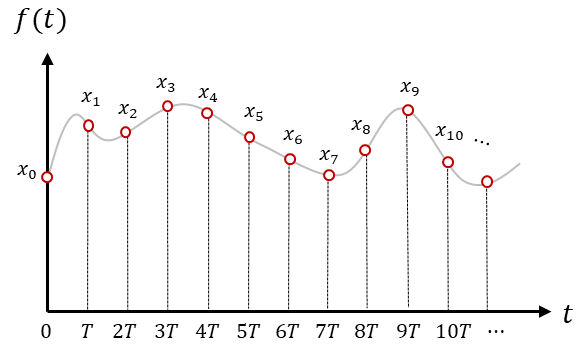
図2　$f(t)のサンプリング$

このサンプリングされたデータを使ってラプラス変換をしてみましょう。
　ラプラス変換のためには連続時間の信号$x(t)$が必要なので以下のように定義してみます。

x(t)
=
\left\{
\begin{array}{ll}
x_n & (t = nT) \\
0 & others
\end{array}
\right.
\tag{7}

ところが(7)式ではラプラス変換の結果は点列$x_n$の値に限らず$0$になってしまいます。これは$x(t)$が離散的であり、積分の中身の関数が図3に示すように幅を持たず、図1のように面積を計算することができないためです。

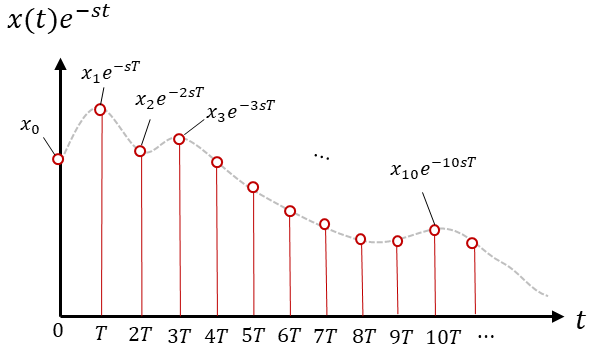
図3　$x(t)$をラプラス変換しようとしたもの

　これは非常にマズいですので、無理やり幅を持たせて積分することを考えてみます。具体的には$x(t)$のラプラス変換を図4に示す長方形の面積の合計であるというふうに考えます。あくまでも近似的なものですので、この「ラプラス変換もどき」は記号$\mathcal{L}'$や$s'$を用いて表すことにします。

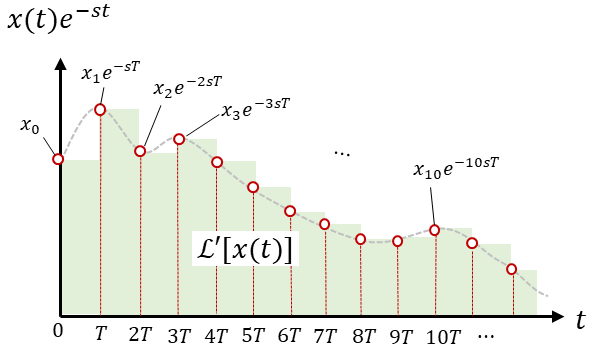
図4　ラプラス変換もどき

　以上のラプラス変換もどきを式に落とし込むと以下のようになります。長方形の面積をすべて足しただけです。

\mathcal{L}'[x(t)]
=
T x_0
+
T x_1 e^{-s'T}
+
T x_2 e^{-2s'T}
+
\cdots
=
T \sum_{n = 0}^{\infty}  x_{n} e^{-ns'T} 
\tag{8}

　ここで

z
=
e^{s'T} 
\tag{9}

とすれば、(8)式はZ変換を用いて以下のように表現できます。

\mathcal{L}'[x(t)]
=
T \sum_{n = 0}^{\infty}  x_{n} z^{-n} 
=
T X(z)
\tag{10}

さらに(10)式の両辺をサンプリング周期$T$で正規化してやると

X(z)
=
\dfrac{\mathcal{L}'[x(t)]}{T}
\tag{11}

となります。言語化すると(11)式は、「Z変換は離散データを無理やりラプラス変換してサンプリング周期$T$で正規化し、データ間の相互作用のみを抜き出したものである」ということを意味しています。要はラプラス変換の離散データ版です。しらんけど。

4. Z変換のシフト操作

　Z変換のシフト操作についてもラプラス変換との対応関係を見ておきたいと思います。Z変換のシフト操作は以下のように表されます。

z\ \mathcal{Z}[x_n]
=
\mathcal{Z}[x_{n+1}] + x_0 z
\tag{12}

(12)式の詳細な導出は付録に書きます。(12)式は「$z$領域において$z$をかけることはデータの参照を1つ先に飛ばすこと」を意味しています($n$番目が$n+1$番目になる)。数学的には初期値$x_0$を考慮しないといけませんが、工学屋さんは入出力関係が分かればなんでもよいのでそんなこと気にしません。
　$s$領域で$s$を書けると微分、$s^{-1}$をかけると積分を意味したのと同じように、$z$領域で$z$をかけると1つ未来のデータへ$z^{-1}$をかけると1つ過去のデータへアクセスできるというイメージが大事です。これらの関係を図5にまとめました。

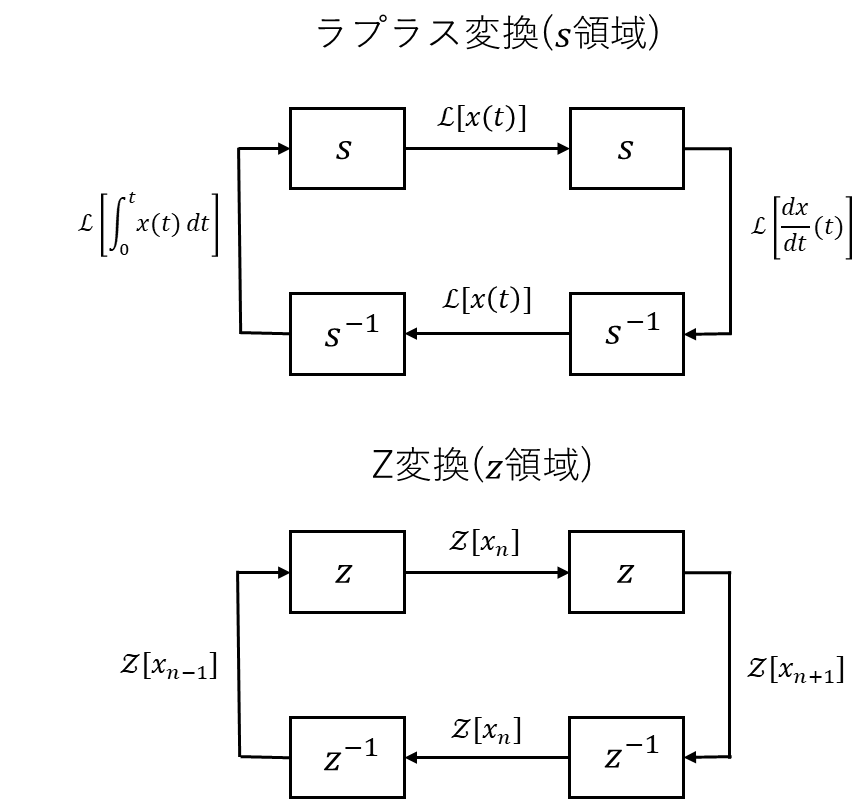
図5　Z変換のシフト操作

本稿ではラプラス変換とZ変換の対応関係を紐解きたいので、「$z$や$z^{-1}$をかける」という操作を$s$領域で考察してみたいと思います。(9)式より、ラプラス変換もどきにおいて$z^{-1}$をかけるという操作は$e^{-s'T}$をかける操作と対応します。$s$と$s'$を同一視する(ラプラス変換もどきをラプラス変換として認めてあげる)とこれはちょうど(4)式のむだ時間要素$e^{-sT}$と考えることができますね！
　まとめると、$z$領域で$z$をかける操作は$s$領域でむだ時間要素をかける操作と対応しており、$z$領域におけるシフト操作は$s$領域における信号のズレとして表現されます。これらのことからもラプラス変換と片側Z変換がうまく対応していることが分かります！

5. おわりに

　本稿では必要に応じて「ラプラス変換もどき」というものを定義し、ラプラス変換とZ変換の対応関係についてフワッとまとめました。むだ時間要素の話ではラプラス変換とラプラス変換もどきが同一であるという仮定をおいて話をすすめましたが、実際には少し誤差が生じます。この誤差はデジタルフィルターを設計する際にカットオフ周波数のズレなどとして現れます。
　この誤差についての話は次回以降にできたらいいなあと考えています。さいごまで読んでいただきありがとうございました！

6. 参考文献

1. 杉江俊治、藤田政之：フィードバック制御入門、コロナ社、2015
2. 荒木光彦：ディジタル制御理論入門、朝倉書店、2015

7. 付録

　Z変換のシフト操作について証明する。片側Z変換の定義より

\mathcal{Z}[x_{n+1}]
=
\sum_{n = 0}^{\infty}  x_{n+1} \ z^{-n}
\tag{a}

となる。ここでシフト操作

k
=
n + 1
\tag{b}

を(a)式に適用し、式変形すると

\mathcal{Z}[x_{n+1}]
=
\sum_{k = 1}^{\infty}  x_{k} \ z^{-(k-1)}

\ \ \ \ \ \ \ \ \  =
z \sum_{k = 1}^{\infty}  x_{k} \ z^{-k}

\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =
\Bigg( z\ x_0\ +
z \sum_{k = 1}^{\infty}  x_{k} \ z^{-k} \Bigg)
-
z\ x_0

\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =
z \sum_{k = 0}^{\infty}  x_{k} \ z^{-k}
-
z\ x_0

\therefore
\mathcal{Z}[x_{n+1}]
=
z\  \mathcal{Z}[x_{n}]
-
z\ x_0
\tag{c}

が得られ、(12)式が導出される。