はじめまして、りょーつといいます。高専出身の大学院2年生です。研究の専門は力学や機構学で、Qiitaでは主に制御工学や数学に関する記事を書いています。最近研究室でデジタル信号処理が流行っているので今週はそれ関連の記事を書いてみました。
目次
1.はじめに
2.ラプラス変換とZ変換の復習
3.双一次変換の必要性
4.双一次変換の導出
5.おわりに
1. はじめに
本稿ではデジタル信号処理に登場する双一次変換についてフワッとまとめようと思います。「制御工学の内容をプログラミングコードに落とし込みたいが、やり方がよく分からない」みたいな方へ刺さる内容になります。制御工学の基礎知識があればより理解しやすいと思います。初期値や数学的な厳密さは重要視しません。
2. ラプラス変換とZ変換の復習
まずはラプラス変換の基本的な性質をおさらいします。ある線形微分方程式をラプラス変換して得られる世界($s$領域)では、$s$をかけることで微分、$s^{-1}$をかけることで積分を表現できます。たとえば(1)式の線形微分方程式は初期値0の条件下でラプラス変換すると(2)式のような形式で記述できるようになります。ちなみにラプラス変換したあとの変数は大文字で表すことが多く、例えば$v(t)$は変換によって$V(s)$と記述されます。
L\dfrac{di}{dt} (t) + Ri (t) + \dfrac{1}{C}\int_{0}^{t} i(\tau) d\tau = v(t)
\tag{1}
LsI(s) + RI(s) + \dfrac{I(s)}{Cs} = V(s)
\therefore
I(s) = \dfrac{Cs}{LCs^2 + RCs + 1}V(s)
\tag{2}
(2)式から(1)式の微分方程式を復元することもできます。
続いてZ変換の基本的な性質をおさらいします。ある差分方程式をZ変換して得られる世界($z$領域)では、$z$をかけることで正のシフト操作、$z^-1$をかけることで負のシフト操作を表現できます。たとえば(3)式の漸化式は初期値0の条件下でZ変換すると(4)式のような形式で記述できるようになります。ちなみにZ変換したあとの変数も大文字で表すことが多く、例えば$y[n]$は変換によって$Y(Z)$と記述されます。
y[n+1] = y[n] + y[n-1] + x[n]
\tag{3}
zY(z) = Y(z) + \dfrac{Y(z)}{z} + X(z)
\therefore
Y(z) = \dfrac{z}{z^2 - z - 1} X(z)
\tag{4}
こちらも同様に、(4)式から(3)式の漸化式を復元することができます。
ラプラス変換は微分積分を簡単な掛け算・割り算で考えられるようにするため、システムの動作を設計する制御工学と相性がいいです。一方で、Z変換は「n個目のデータ」と「n+1個目のデータ」の関係性を説くため、プログラミングと相性がいいです。
3. 双一次変換の必要性
実際にシステムを設計して動かすためには制御系設計とプログラミングの両方の操作が必要になります。前章で、ラプラス変換は制御系設計と、Z変換はプログラミングと相性が良いという話をしました。つまり、この2つの関係を結ぶような変換が必要というわけです。
たとえば$s$領域で入力$U(s)$から$Y(s)$を出力するシステム$P(s)$を設計したとします。このシステムのブロック線図は図1のようになります。

図1 $s$領域のブロック線図
図1のシステムをプログラミングで実装するためには、入力される信号をサンプリングした$u[n]$と出力結果$y[n]$の関係性を明らかにする必要があります。言い換えれば$P(s)$をもとに等価な動作を行う伝達関数$P(z)$を$z$領域で作る必要があります。これは伝達関数$P(z)$をつくることで設計したシステムの動作を行うような漸化式(データ間の関係性)を復元することができるためです。
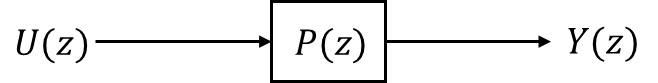
図2 $z$領域のブロック線図
このように$s$領域の伝達関数を$z$領域の伝達関数へ改造するような変換の1つとして「双一次変換」がよく使用されます。双一次変換は以下の式で表されます。
s(z) = \dfrac{2}{T} \dfrac{1 - z^{-1}}{1 + z^{-1}}
\tag{5}
$T$はデータのサンプリング周期です。(5)式の詳しい導出は次章で行います。とりあえず本章では以下に示すシステム実装の流れをおさえておいてください。
① 制御工学を駆使して伝達関数$P(s)$を設計する。
② 双一次変換を使って、伝達関数$P(s)$を離散化し、伝達関数$P(z)$を作る。
③ $P(z)$から漸化式を復元し、プログラミングで実装する。
4. 双一次変換の導出
双一次変換の導出のために、図3に示す簡単な積分システムを考えます。入力$u(t)$が与えられるとその関数を定積分した出力$y(t)$が出力されるというものです。ただの積分ですので$s$領域では以下のように表現されます。
Y(s) = \dfrac{1}{s}\ U(s)
\tag{6}
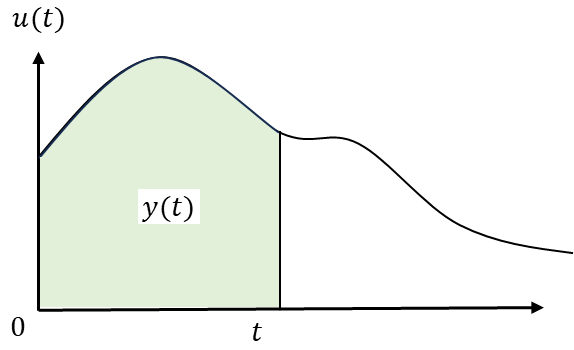
図3 積分システム
次に図3のシステムを離散化して考えてみます。図4のような台形近似を使うとすると、$n$個目の出力$y[n]$は以下のような漸化式で表現できます。
y[n] = y[n-1] + \dfrac{T}{2} \Big(u[n-1] + u[n]\Big)
\tag{7}

図4 台形近似による積分の表現
ただし$T$は入力信号$u(t)$のサンプリング周期、あるいはシステムの制御周期です。漸化式が得られたので(7)式をZ変換してみましょう。負のシフト操作は$z^{-1}$を掛けることで表現できるので以下のような結果が得られます。
Y(z) = z^{-1}Y(z) + \dfrac{T}{2} \Big(z^{-1} U(z) + U(z)\Big)
\therefore
Y(z) = \dfrac{T}{2} \dfrac{1 + z^{-1}}{1 - z^{-1}}U(z)
\tag{8}
(6)式と(8)式の入力・出力を同一視して、伝達関数の部分を等号で結ぶと双一次変換が得られます。
\dfrac{1}{s} = \dfrac{T}{2} \dfrac{1 + z^{-1}}{1 - z^{-1}}
\therefore
s(z) = \dfrac{2}{T} \dfrac{1 - z^{-1}}{1 + z^{-1}}
\tag{9}
前章でも述べたとおり、システムの離散化という点において双一次変換はよく用いられます。デジタル信号処理やデジタル制御理論などを学ぶときに必須のスキルとなります。
実際には(9)式のように$s$領域と$z$領域の入力・出力を同一視した関係上、離散化による誤差が発生します。この誤差はフィルターを設計する際などに、周波数応答のズレなどとして現れます。(この話はまた後ほど)
双一次変換は積分を台形近似によって離散化することで得られました。ちなみに長方形近似することでも同様の操作を得ることができ、これを「後退差分近似」と呼ぶことが多いです。ちなみに後退差分近似の変換公式は以下のように表されます。
\therefore
s(z) = \dfrac{1-z^{-1}}{T}
\tag{10}
(10)式も双一次変換と同様の手順で証明できます。双一次変換よりも簡単なので自分でやってみてください。
5. おわりに
本稿ではシステムの実装に必要なラプラス変換とZ変換をつなぐ「双一次変換」についてフワッと解説しました。次回の記事では双一次変換を使って一次ローパスフィルタを設計する手法についてまとめる予定です。最後までよんでいただきありがとうございました!