はじめまして、りょーつといいます。高専出身の大学院2年生です。研究の専門は力学や機構学で、Qiitaでは主に制御工学や数学に関する記事を書いています。研究室でデジタル信号処理が流行っているので最近はそれ関連の記事を書いています。今週は3本目です。以前までの記事は以下のリンクからどうぞ。
デジタル信号処理① ラプラス変換とZ変換の関係性
デジタル信号処理② 双一次変換の必要性とイメージ
目次
1.はじめに
2.ローパスフィルタの伝達関数
3.双一次変換による伝達関数の離散化
4.おわりに
1. はじめに
本稿ではデジタルローパスフィルタの実装についてフワッとまとめようと思います。制御工学やフィルターの基礎知識があればより理解しやすいと思います。先に結論を述べると、フィルターへの入力信号データを$u_n$、フィルターの出力信号データを$y_n$としたとき、
y_n = y_{n-1} + \dfrac{\Delta t}{2T + \Delta t} \big( u_n + u_{n-1} - 2y_{n-1} \big)
\tag{1}
という計算式をプログラムに組み込むことで1次ローパスフィルタが実装できます。ただし、$T$はローパスフィルタの時定数、$\Delta t$は入力信号データのサンプリング周期です。
2. ローパスフィルタの伝達関数
まずはローパスフィルタのおさらいをします。ローパスフィルタはその名のとおり、ロー(周波数の小さい信号)をパス(通過)させるようなシステムです。信号に生じた高周波のノイズを除去するためなどに使用されます。ローパスフィルタの伝達関数$G(s)$は
G(s) = \dfrac{1}{1 + Ts}
\tag{2}
と表されます。ブロック線図で書くと図1のようになります。(2)式の$T$はフィルターの時定数を表しており、カットオフ周波数(除去したい周波数の境界値)$f_c$との関係は以下のように表されます。
T = \dfrac{1}{2 \pi f_c}
\tag{3}
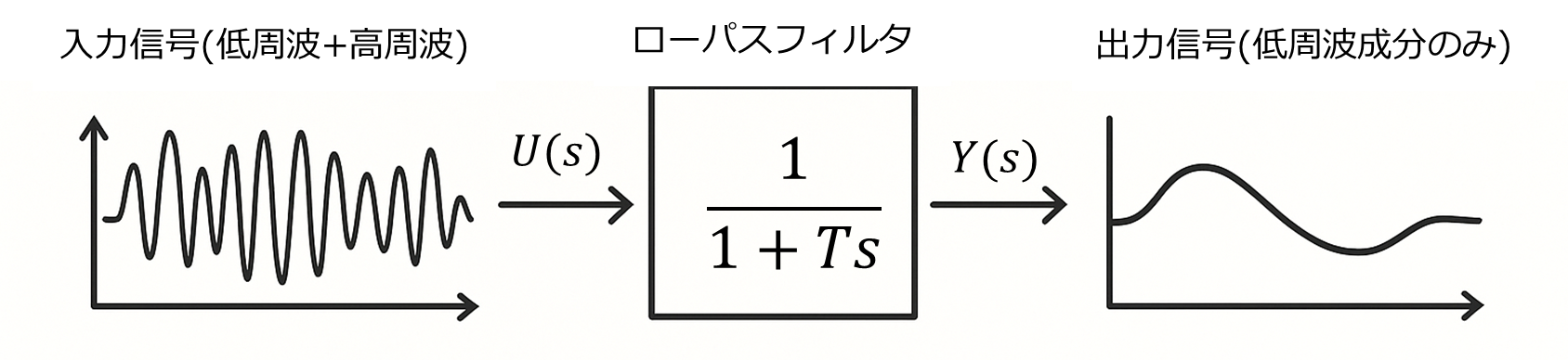
図1 $s$領域における1次ローパスフィルタのブロック線図
入力信号が時間的に連続的である&フィルターの構成要素も時間的に連続的であれば上記のローパスフィルタの実装は容易です。スイッチのチャタリング対策などに用いられるRCフィルタなんかはその代表例です。
しかし、入力信号が離散的にサンプリングされたものであったり、フィルターの動作をプログラムによって構成することになったりすると、伝達関数を離散的に表現する必要性が出てきます。たとえば「ロボットの制御をするときに、センサの高周波ノイズを除去したい」みたいな用途だと、離散化の操作は避けられません。次章からは(2)式の伝達関数を離散化する手法について解説していきます。
3. 双一次変換による伝達関数の離散化
本章ではローパスフィルタの伝達関数を離散化し、プログラムに実装する手法について説明していきます。$s$領域の伝達関数を手っ取り早く離散化する手法として「双一次変換」というものが良く使われます。フワッと説明すると、$s$領域の伝達関数$P(s)$に対して
s = \dfrac{2}{\Delta t} \dfrac{1 - z^{-1}}{1 + z^{-1}}
\tag{4}
を代入するだけで離散化された伝達関数$P(z)$が作れるよって変換です。$\Delta t$はサンプリング周期もしくは制御周期を意味しています。詳しくは前回の記事を参照ください。
ここでは(4)式を信じて(2)式の離散化をしてみようと思います。(4)式を(2)式に代入し、整理すると
G(z)
=
\dfrac{1}{1 + \dfrac{2T}{\Delta t} \dfrac{1 - z^{-1}}{1 + z^{-1}}}
=
\dfrac{\Delta t \big( 1 + z^{-1} \big)}{\Delta t \big( 1 + z^{-1} \big) + 2T \big( 1 - z^{-1} \big)}
\tag{5}
となります。これを$z$領域でみた入力信号データ$U(z)$と出力信号データ$Y(s)$の関係に代入し、整理すると
Y(z) = G(z)U(z) = \dfrac{\Delta t \big( 1 + z^{-1} \big)}{\Delta t \big( 1 + z^{-1} \big) + 2T \big( 1 - z^{-1} \big)} U(z)
\therefore
Y(z)
=
z^{-1}Y(z) + \dfrac{\Delta t}{2T + \Delta t} \big( U(z) + z^{-1}U(z) - 2z^{-1}Y(z) \big)
\tag{6}
あとはZ変換のルールに沿って(6)式から漸化式を復元すると1次ローパスフィルタを表現した式
y_n = y_{n-1} + \dfrac{\Delta t}{2T + \Delta t} \big( u_n + u_{n-1} - 2y_{n-1} \big)
\tag{7}
が導出されます。
(7)式をExcel上で実装して描画したものが図2~図4となります。入力信号は
u(t) = 10\sin{\bigg( \dfrac{2t}{3} \bigg)} + 5 \cos{(100 t)}
\tag{8}
であり、サンプリング周期は$0.01$ [s]としています。時定数$T$は図によって異なります。これらの結果から、時定数$T$が大きいほど信号が減衰し、位相がズレていくことがなんとなく分かります。これらの詳細(周波数解析)については次回解説しようと思います。

図2 時定数$T = 0.02$の場合の入出力関係
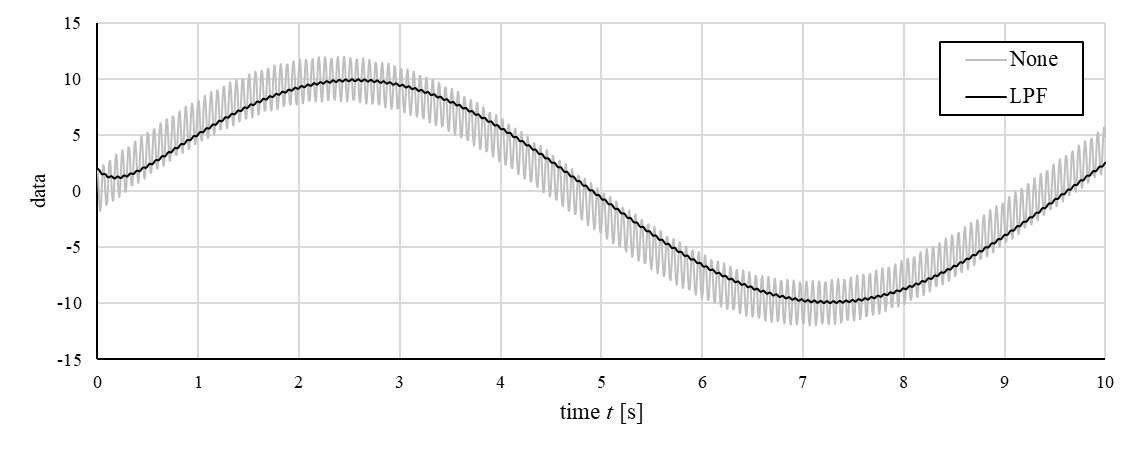
図3 時定数$T = 0.2$の場合の入出力関係

図4 時定数$T = 2$の場合の入出力関係
4. おわりに
本稿では双一次変換を用いた1次デジタルローパスフィルタの実装についてフワッとまとめました。また、Excelを用いた軽い実験により、設計したフィルターがそれっぽい動作をすることを確認しました。気になる周波数解析については来週解説する予定です。
最後まで読んでいただきありがとうございました!