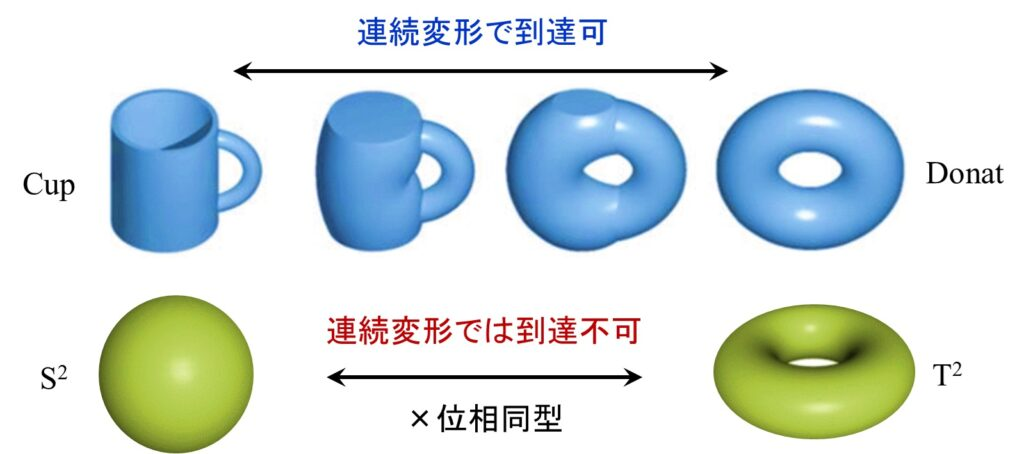
背景
- 最近案件で3Dデータに触れることが多く、その中で「トポロジー」という単語が出てくることが多い。
- 素粒子理論の分野でもトポロジーが頻出しており、人並み以上には詳しいと自負しているが、3Dデータのデザインの分野では、どのようにトポロジーが求められているのか気になった。
参考:素粒子理論におけるトポロジー
この章は読み飛ばして良いです
ここは私が好きでまとめた部分であり、未学者はわからない (わからせようとする気もなく書いた) 部分なので、読み飛ばしてください。
例1:Seiberg-Witten曲線
4次元$\mathcal N=2$ 超対称性理論(それぞれの粒子に2種類の超対称ペアが存在しているような理論)が、ある複素曲線(Riemann面)で特徴づけられることが知られている。そのRiemann面を描写する複素方程式を、Seiberg-Witten曲線と呼ぶ。
例:SU(2) pure Yang-Mills理論のSeiberg-Witten曲線
$$
\Sigma: y^2 = x^3-ux+ v
$$
そのRiemann面上の非自明なサイクル$\gamma$ (1 次ホモロジー群の要素$\gamma\in H_1(\Sigma;\mathbb Z)$)上で、対応する微分要素$\lambda$(1 次コホモロジー群の要素 $\lambda\in H^1(\Sigma;\mathbb C)$)を周回積分することで、理論に存在する粒子の電荷や質量が計算できる。
$$
Z = \oint_\gamma \lambda
$$
例2:超重力理論(多様体・ホモトピー)
超弦理論をもとに考えられる超重力理論は10次元なため、4次元時空(時間+3次元空間)+6次元のコンパクト空間に分けて考えられることが多い。
$$
\mathcal M_{10} = \mathbb R^{1,3}\times CY_3
$$
$CY_3$:6次元Calabi-Yau多様体。超重力理論では、6次元空間が閉じた空間(コンパクト空間)となっており、4次元時空にいる我々からは存在が確認できないと考える。
素粒子理論では10次元空間を「メトリック」と呼ばれる、微分要素$dx^\mu$で記述することが多い為、多様体として空間を捉えることが多い。
$$
dx = g_{\mu\nu}dx^\mu dx^\nu
$$
$g_{\mu\nu}$: メトリックテンソル。超弦理論では「重力子」として扱われることも多い。
6次元コンパクト空間の幾何構造によって、4次元時空上の理論が変化する。特に、以下のようなコホモロジーとの関係性がある。
- ベクトル多重項(光子のような、力を伝える粒子と超対称ペアが入ったセット)の数
$$
N_\text{vector}=\dim H^{1,1}(CY_3)
$$ - ハイパー多重項(クォークのような、物質を形成する粒子と超対称ペアが入ったセット)の数
$$
N_\text{hyper}=\dim H^{2,1}(CY_3)+1
$$
3Dデータにおけるトポロジー
前提
3Dデータの表現形式
ポリゴンメッシュ
- 頂点・辺・面(三角形や四角形)の組合せで表現される離散的な曲面
- 接続関係(どの頂点がどの辺に属し、どの辺がどの面に属するか)が明示的にデータ構造として保持される
- 多様体性や穴の有無など、トポロジー的性質を直接読み取りやすい表現形式

3Dメッシュの例(https://qiita.com/u_1roh/items/fe588af9fe014c573af6)
B-rep(Boundary Representation)
- 立体を、その外側の境界曲面の集合として表現する方式
- 位相要素(面・辺・頂点の接続関係)と幾何要素(実際の曲線・曲面)を分離して管理する
- CADシステムの内部表現として広く用いられており、後述のメッシュや配管モデルの基盤となる

B-repの例(https://qiita.com/EdgeDevice/items/bc7250bed3bf7d20d924) - B-rep における位相要素
- ボディ(body)
- 個々のソリッド全体を表す単位
- シェル(shell)
- ソリッドの外側の境界面集合(閉曲面全体)
- フェイス(face)
- 個々の曲面パッチに相当する領域
- エッジ(edge)
- ループを構成する境界線分(曲線)
- バーテックス(vertex)
- エッジの端点
- ループ(loop)
- フェイス境界の輪郭(外側ループおよび穴の内側ループ)
- ボディ(body)
- B-rep における幾何要素
- ポイント(point)
- 3次元空間上の座標
- 曲線(curve)
- 3次元空間上のパラメトリック曲線
- 曲面(surface)
- 3次元空間上のパラメトリック曲面(NURBSなど)
- ポイント(point)
- フィーチャ(feature)
- 押し出し、回転、穴あけ、面取りなど、設計意図に沿った形状操作の単位
- 個々のフィーチャが、B-rep の位相構造(フェイスの追加・削除、穴の生成など)にどのような影響を与えるかが問題となる
CSG(Constructive Solid Geometry)
- 原始形状(プリミティブ)に対してブーリアン演算(和・差・積)を繰り返して物体を構成する表現
- B-rep と相互変換されることが多く、その際にトポロジー構造が変化する
トポロジーの基本概念
位相同型
- 連続な全単射かつその逆写像も連続である対応
- 互いに位相同型な空間は「同じトポロジーを持つ」とみなす
連結性
- 空間が二つの非自明な開集合に分解できない性質
- 3Dデータの文脈では、「1つの物体がいくつの連結成分に分かれているか」が重要となる
多様体
- 局所的にはユークリッド空間と同相である空間(地球上にいる我々には、地面が平面に見える)
- 3Dデータでは、物体の境界が2次元多様体として埋め込まれているか(manifoldかどうか)が重要となる
境界付き多様体
- 各点の近傍が、ユークリッド空間そのものではなく半空間に同相である点を含む多様体
- 開いたメッシュや切断面を持つモデルは、境界付き多様体として扱われる
種数(genus)
- 直観的には「独立な穴の数」を表す不変量
- B-repやメッシュモデルの整合性検査や、トポロジー制約付き最適化において参照される
オイラー標数
- 多面体等に対し、以下のように定義される不変量
$$
\chi = \text{(面の数)} - \text{(辺の数)} + \text{(頂点の数)}
$$- 種数0・境界なし・射影平面でない多様体(立方体、三角錐など)はオイラー標数が2になる。
- メッシュやセル複体に対して一般化され、種数と関係付けて用いられる
manifold / non-manifold
- 各点近傍が多様体になっている場合を manifold と呼び、そうでない場合を non-manifold と呼ぶ
- メッシュデータにおいて、non-manifold な頂点・辺(例えば1本の辺に3枚以上の面が集まる場合)は、CADやCAE、3Dプリントで問題の原因になりやすい
配管・配線の用語
ノード(node)
- 配管・配線ネットワークの接続点
- 機器のポート、バルブの接続口、電気コネクタの端子などが含まれる
エッジ(edge)
- ノード間を接続する配管セグメントやケーブルセグメント
- 直線区間だけでなく、曲線や複数の曲げを含む場合も一つのエッジとして扱うことがある
ルート / 経路(route / path)
- 特定の二つのノード間を結ぶエッジの列
- 自動配管・自動配線アルゴリズムは、評価関数に基づいてルートを探索する
ブランチ(branch)
-
配管・配線ネットワークにおける分岐部分
-
あるノードを境に複数方向へエッジが伸びる構造
ループ(loop)
-
始点と終点が同じ閉路
-
ループを許すかどうかは、対象システム(配水、配電、プロセス配管など)により異なる
ネット / ネットリスト(net / netlist)
-
接続すべきノード集合と、その結び方に関する論理的仕様
-
電子回路設計では標準的な概念であり、配管・配線CADでも類似の考え方が用いられる
論理トポロジー / 物理トポロジー
-
論理トポロジー
- どのノードがどのノードと接続されるべきかという抽象的な接続関係
-
物理トポロジー
- 3次元空間内で実際にどの経路を通すか(障害物・標高・設備配置を考慮したもの)
どのようにトポロジーが出てくるのか?
3Dデータの分野では、素粒子理論のようなホモロジー群・コホモロジー群のような数学的な要素よりかは、「そのデータが持つ情報・特徴量」として管理されている印象。
メッシュ・B-Repの接続情報
B-Rep・メッシュでは、トポロジー(接続情報)とジオメトリ(形状)の情報を分けて持っている。**トポロジーとジオメトリーを分けて管理することで、頂点の位置をずらす、面の形を変えるなど、ジオメトリーを変形しても接続構造を保ったまま編集することが可能になる。
- トポロジー:何がどこにつながっているかという情報
- Vertex(0次元) / Edge(1次元) / Face(2次元)と、それらの包含関係(Contains / Bounded by)
- B-Repでは、Faceの集合としてのShellや、Shellの集合としてのBodyといった上位の位相要素も定義される。
- ジオメトリー:
- 頂点に対応する座標(Point)
- 辺に対応する曲線(Curve)
- 面に対応する曲面(Surface)

B-repのトポロジー・ジオメトリー(https://www.researchgate.net/figure/Overview-of-the-BREP-structure-The-data-model-contains-topological-entities-highlighted_fig6_281086863)
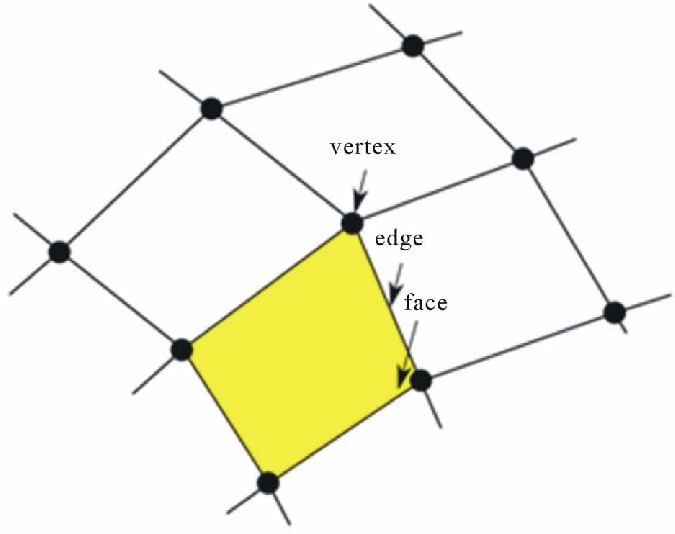
メッシュのトポロジー(https://www.researchgate.net/figure/Mesh-elements-vertex-edge-and-face_fig3_272666473)
図からもわかるように、トポロジーは有向グラフとして管理しやすいため、3DデータをグラフDBで管理することも多い。

https://qiita.com/EdgeDevice/items/bc7250bed3bf7d20d924
オイラー操作
オイラー操作とは、位相構造を壊さずに編集するための基本操作である。 位相構造を変えないためには、オイラー標数を変えないように変形を行われなければならない(頂点を加えたいなら、それに応じて辺・面も追加しなければならない)。
多様体性とwatertight性
実務上「きれいなソリッド」として扱いたい場合、多くのツールは「2 次元多様体かつ watertight」であることを暗黙の前提にしており、この条件から外れるモデルは、まずクリーンアップ(修復)の対象とされる。
多様体性
多様体性とは、3Dデータが多様体になっているかを指す。
- 内部エッジに隣接する面の枚数が2枚以下か?
- 境界エッジに隣接する面の枚数は1枚か?
- 頂点まわりの面が 1 つの輪になっているか(扇形のように分断されていないか)?
これらが満たされていないと、その部分は局所的に見た時に平面空間として扱えず、non-manifolとなり、法線計算、パラメータ化、リメッシング、ブーリアン演算などで不具合を起こす。
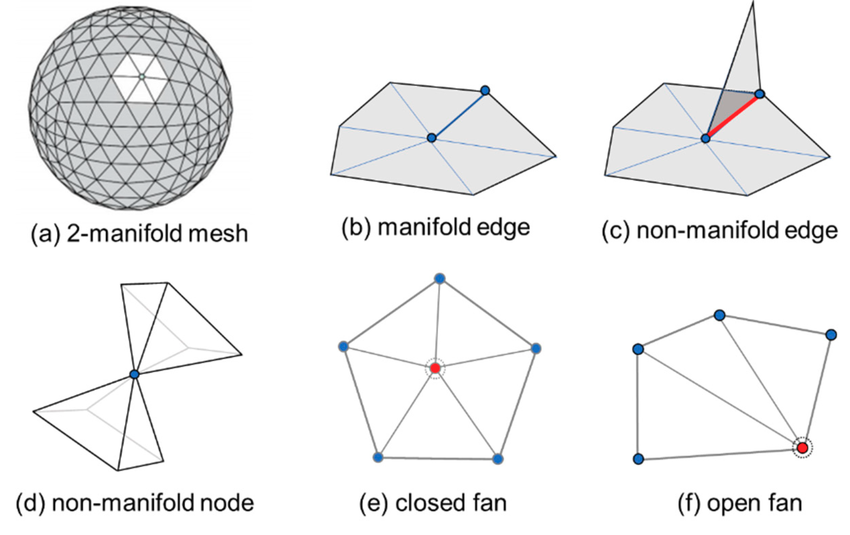
https://www.researchgate.net/figure/Manifold-definitions-a-A-3D-triangular-mesh-of-a-sphere-with-512-triangles-b_fig1_337698839
watertight性
watertight性とは、水が漏れないか、のように境界が隙間なく閉じていて、内部と外部をきちんと分ける 3D 形状になっているかを指す。
- すべてのエッジがちょうど 2 枚の面に共有されているか?
- 面と面の間に隙間や重なりがないか?
- 法線の向きが一貫しており、内部と外部が区別できるか?
CAE や光学シミュレーションのベンダは、非 watertight なメッシュがあると、レイが穴から漏れたり、体積の判定が失敗してエラー率が高くなる。

終わりに
- もっと数学的な計算を期待していたので、ちょっと残念
- この記事がかなり参考になりました https://qiita.com/u_1roh/items/fe588af9fe014c573af6