3D CAD の内側をちょっと覗いてみませんか

3Dの数学や技術というと、パッと思い浮かぶのはゲームや映画のCGといったグラフィックス系ではないでしょうか。

私は3D CADや製造業の周辺でソフトウェア開発の仕事をしています（3D CADそのものの開発はやっていなくて、その周辺の開発という感じです）。製造業でも3Dの技術は大いに活用されているのですが、その技術情報がオモテで（ネットで）語られる機会は少ないという印象です。ゲームやVRといった分野はUnityなどと絡めた技術記事をよく目にしますが、CADの技術記事はなかなか目にしないですね。

そんなわけで、ここではグラフィックスとはやや違う視点で、コンピュータでモノの形を表現する方法についてざっと紹介してみたいと思います。（といっても一部しか紹介できませんでした。なかなか軽く広く全体を紹介するというのは難しい…）

ガチな数学記事ではなく（そもそも私にはそんな記事を書く実力はない）、読み物として気楽に流し読み出来る記事を目指します。

メッシュと多様体

まずはポリゴンメッシュから始めましょう。ものづくりの世界でもメッシュはもちろん使われています。分かりやすいところでは、最近はすっかりブームが冷めてしまった（？）3Dプリンタとかですね。

特にすべての面が三角形で構成された三角形メッシュを扱うことが多いです。これは数学的には「単体複体」と呼ばれるものだと思います。しかし私はその言葉を厳密な定義に基づいて正確に運用できる自信がないので、以下でも「メッシュ」で通すことにします。

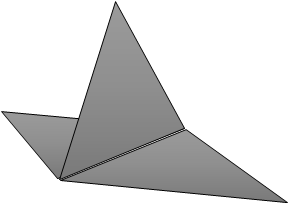
ものづくりでは最終アウトプットは物理的な「物体」です。物体の表面は（向き付け可能な）2次元多様体になります。

本来「多様体」という言葉は非常に抽象的な数学的概念かと思いますが、この分野では形状データの特徴を指す具体的な言葉として割りとカジュアルに使われているように思います。

（メッシュの例）

後で少しだけ紹介する3D CADのデータ構造も、メッシュのデータ構造や知識が基礎基本となります。

非多様体メッシュ

次のようなメッシュは「非多様体メッシュ」と呼ばれます。

多様体であるためには、形状の任意の点の開近傍が $R^2$ の開円板と同相でなくてはなりません。上図のようなT字型のジョイントではその条件を満たなさいので、非多様体と呼ばれます。

こういうメッシュを3Dプリンタに入れるとエラーになったりおかしな形状が出力されたりします。建築パースのCG用モデルや3Dキャラクタのモデルなどのデータには、こういった非多様体形状を含むものが多く見られる印象です。3Dプリンタブームの頃に「3Dデータさえあれば簡単に模型が作れる！フィギュアが作れる！」みたいな機運もありましたが、この辺の事情もあって期待されたほどうまくは行かなかったのではないでしょうか（もちろん、知識と技術を持っていて上手に活用している方たちや企業も沢山いらっしゃいます）。なお、3D CADで作られたデータ、特にソリッドモデラーと呼ばれる種類のCADで作られたデータでは、こういった非多様体形状が含まれることはありません。

現実と戦うためにはこういうデータとも向き合う必要がありますが、以下ではキレイな多様体メッシュだけを考えていきます。

多様体メッシュが作るグラフ

向き付け可能な多様体メッシュの要素（頂点、エッジ、面）が作るグラフ構造について考えてみます。
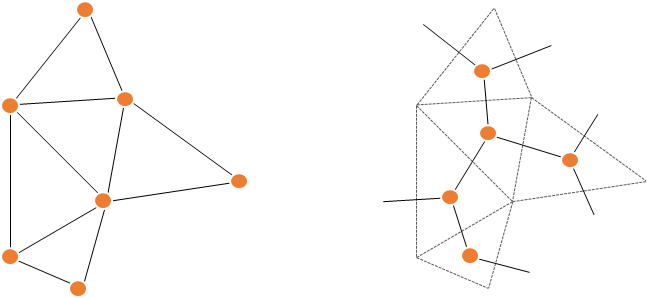
これがなかなか面白くて（と僕は思っているのですが）、2種類の双対なグラフが埋め込まれた構造をしています。

1つは、頂点をノードとして、エッジがノードとノードを繋いで作るグラフです。これはメッシュをワイヤーフレーム表示した図に一致するので分かりやすいかと思います。

もう1つは、面をノードとして、エッジが左右の面を繋いで作るグラフです。面と面はエッジを介して隣接していますから、この接続関係もグラフとして考えられます。

更に、面には向きの概念があります。面の向きというのは、頂点の並び順が反時計回りに見える方を表（オモテ）と定義されます。メッシュが向き付け可能な多様体となるためには、隣接する面同士で向きが揃っている必要があります。

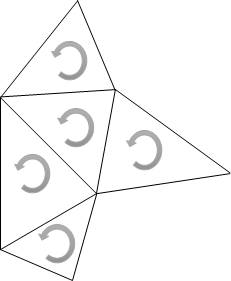
こういった要素間の接続情報を「位相情報」とか「位相要素」などと呼びます。物体の形状そのものとは異なる、トポロジカルな情報といえるかと思います。

さて、この「位相情報」をうまく表すためのデータ構造があります。それが次で説明する「ハーフエッジ構造」です。

ハーフエッジ構造

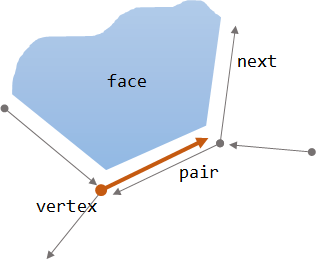
ハーフエッジ（half-edge）とはその名の通り、「半分にしたエッジ」です。ハーフエッジのペアで1本のエッジが表現されます。

まず、面のループ（反時計回り）をハーフエッジのリンクリストで表現します。

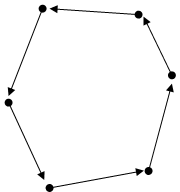
次に、2つの面が隣接するハーフエッジを貼り合わせてペアにします。

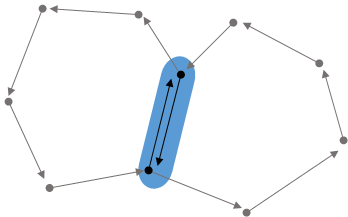
ハーフエッジをC言語の構造体で表現すると次のようになります。（こういうとき何の言語で書くのがいいんでしょうかね？）

struct Halfedge {
  Vertex* vertex;
  Face* face;
  Halfedge* next;
  Halfedge* pair;
};

Halfedge* he に対して次の条件が成立します。

• he->pair->pair == he
• he->face == he->next->face
• he->next->vertex == he->pair->vertex

無駄がなくて、とても見事なデータ構造だなぁと思います。

オイラー操作

以上で多様体メッシュがハーフエッジ構造で表せることが分かりました。ここでは、そのメッシュに対する変更操作を考えていきます。リンクリストや二分木といったデータ構造に対して要素の追加や削除の操作が定義されるのと同様に、ハーフエッジ構造に対して要素（頂点、エッジ、面）を追加したり削除したりする操作を考えるのです。それが「オイラー操作」と呼ばれるものです。

オイラー操作という名前は、お気づきの方も多いと思いますが、オイラーの公式 オイラーの多面体定理に由来しています。オイラーの公式 オイラーの多面体定理は次式で表されます。

v - e + f = 2(1 - g)

ここで $v$ は頂点数、$e$ はエッジ本数、$f$ は面数、そして $g$ は種数（genus）と呼ばれるもので、簡単に言うとドーナツの穴の数です。(シェルの数は1としました）
この式については色々なところで解説されているのでここでは説明を省きます。それにしても、この式を初めて知ったときは感動したものです。何万頂点もあるようなメッシュデータでも、計算してみるときちんとこの式が成立していることが確認できます。アタリマエのことかもしれないのですが、「数学ってすげーなぁ…」と思った覚えがあります。

さてさて、話をオイラー操作に戻しましょう。オイラー操作とは、このオイラーの公式を保ったまま要素を追加したり削除したりする操作です。例えば、頂点だけを1つ追加するという操作はやってはいけないわけです。そんなことをしたらオイラーの公式から逸脱してしまうわけで、それはつまり正当な多様体メッシュではなくなってしまうということです。

オイラー操作の例として、1本のエッジを分割して頂点を1つ挿入する、という操作を考えます。これは $v$ と $e$ が1つずつ増えますが、$f$ は変わりません。この増減はきちんとオイラーの公式に従っていることが容易に確認できます。複雑な形状編集操作もこういったプリミティブなオイラー操作の組み合わせで表すことにより、位相を不正な状態に壊してしまうことを避けることが出来ます。

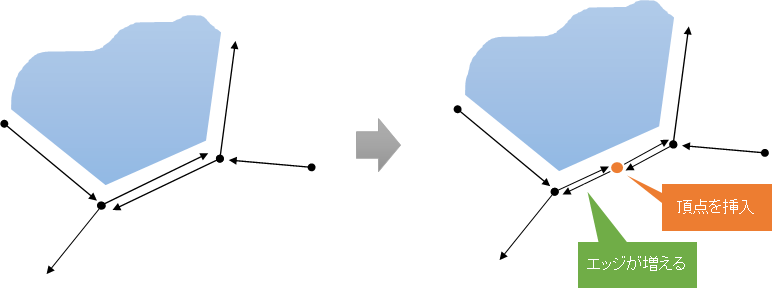
三角形メッシュのオイラー操作

特に実用的な例として、三角形メッシュに限定したオイラー操作を考えてみます。

まずはオイラーの公式を三角形メッシュに限定したものに変形することを考えましょう。三角形メッシュでは、すべての面は3本のエッジを持ちます。一方で1本のエッジは両隣の三角形に共有されていることを考慮すると、次式が成り立つことがわかります。

e = \frac{3}{2}f

これをオイラーの公式に代入すると次式が得られます。

2v - f = 4(1 - g)

ちょっと余談になりますが。$g$ の値は $v$ や $f$ と比べてずっと小さいことが多いです。そのような三角形メッシュでは概ね $f\simeq 2v$ が成り立ちます。以前、仕事相手の方に「そのメッシュの大まかな頂点数を教えてください」と伝えたところ「使っているソフトには面数しか表示されていないので頂点数が分かりません」と返答頂いたことがあったのですが、面数を2で割るだけで大まかな頂点数は分かるというわけです。

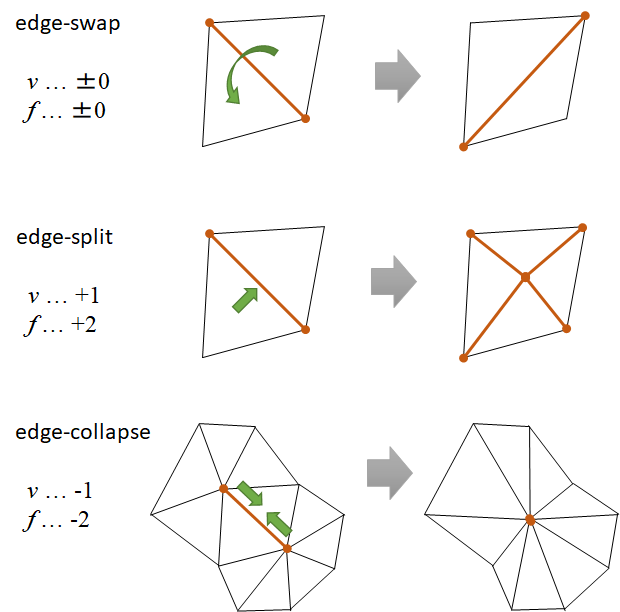
さてさて。三角形メッシュで使われるオイラー操作は主に次の3つです。

例えばメッシュのリダクション（間引き）処理などは、edge-collapse 操作を繰り返し適用する形で実装したりします。

ソリッドCADと B-rep 構造

さて、ようやくCADの話です。

3D CAD には大きく分けてサーフェスモデラーとソリッドモデラーの2種類がありますが、ここではソリッドモデラーの話をしましょう。ソリッドモデラーは、上で説明したような位相情報を備えたCADシステムです。そのデータ構造は「B-rep（ビーレップ）構造」と呼ばれます（検索してみると表記ゆれがあるようで、BREPとかBrepという表記も見つかります）。B-rep とは Boundary Representation の略で、日本語では「境界表現」と訳されます。

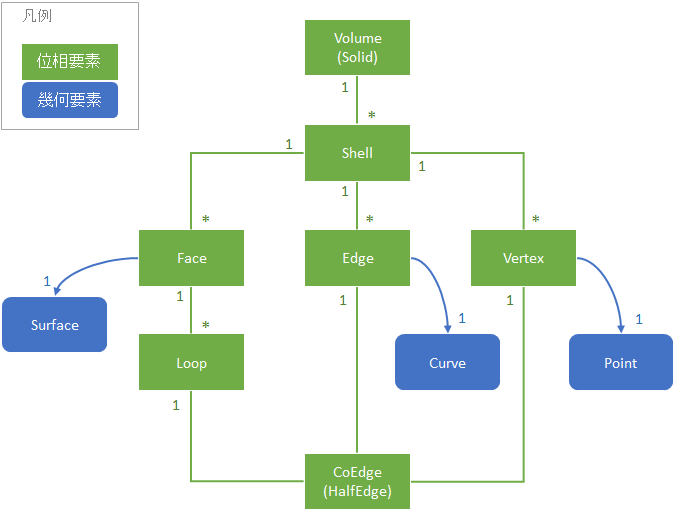
B-rep を構成する要素には、大きく分けて次の2種類があります。

• 位相要素（トポロジー要素） … 頂点、エッジ、フェース、シェルなど。形状そのものではなく、形状を構成する要素の「つながり」（＝グラフ構造）を表現するデータ構造。
• 幾何要素（ジオメトリー要素）… 曲線や曲面といった、形状そのものを数式で表現したもの。直線、円弧、円筒面などといったシンプルなものに加えて、Bezier、B-Spline、NURBSといったパラメトリック表現によるものがある。

位相要素は、今まで説明してきたポリゴンメッシュの位相要素と大きくは違いません。概ね同じと考えて結構です。ただし一つだけ、ポリゴンメッシュにはなかった種類の位相要素が B-rep にはあります。

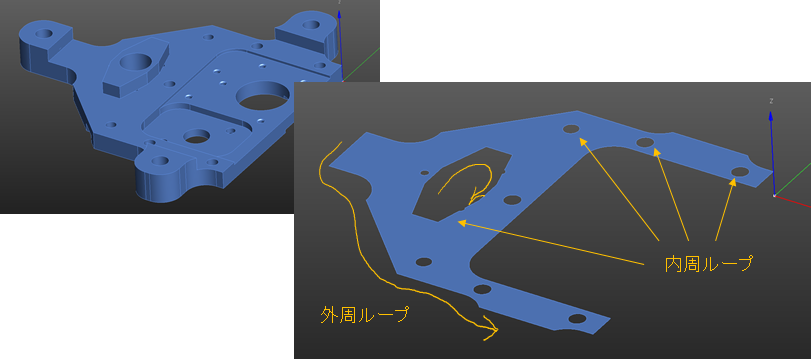
それは「ループ」要素です。B-rep 構造ではフェースの境界ループは1つとは限らないのです。

ループの数を $l$ とします。ループ要素を加味して Euler の式 オイラーの多面体定理を拡張した式があります。

v - e + f - (l - f) = 2(1 - g)

ポリゴンメッシュと同様に、B-rep においてもオイラー操作が定義されます。ソリッドモデラーは核となる部分にソリッドカーネルと呼ばれるライブラリを持っており、形状編集操作はすべてオイラー操作を通して行われるように設計されているのです。

NURBS曲線

今までは位相要素（トポロジー）の話ばかりをしてきました。ここでは話題をガラッと変えて、幾何要素（ジオメトリー）の代表選手であるNURBSについて紹介します。

NURBS とは Non-Uniform Rational B-Spline （非一様有理Bスプライン）の略です。「ナーブス」と発音するのが一般的です。ときどき「ナーバス」と発音される方がおられるのですが、そんなに神経質にならなくても大丈夫ですｗ

Bスプライン曲線については、詳細はともかくとして名前は聞いたことがある方も多いのではないでしょうか。またベジェ曲線というのも耳にしたことがあるかと思います。NURBS曲線はこれらをより一般化したもので、Bスプライン曲線もベジェ曲線もNURBSに包含されてしまいます。その「マジック」を実現しているのが Non-Uniform の部分になります。

しかし Non-Uniform の話は「ノットベクトル（knot vector）」という面倒なものが出てきて、お手軽に紹介するのがちょっと難しいのです（などと言い訳をして説明を逃げます）。それよりも、ここではNURBSのもう一つの特長である「有理（Rational）」の部分にフォーカスしてみましょう。個人的にはこちらのほうがより手軽に "Aha!" を味わえると思います。

有理式で円弧を表す

NURBS曲線は円弧も表現できます。このカラクリが今から説明する「有理（Rational）」の部分になります。

ここでは簡単のため3次元空間ではなく2次元平面上で曲線を考えることとし、曲線の種類もベジェ曲線を例にとって話を進めます。しかし同様の議論は3次元空間でもNURBSでも成り立つので、特に条件を限定した議論というわけではありません。

さて、2次のベジェ曲線を考えましょう。ベジェ曲線は次式の形で書けます。

\begin{array}{rl}
\vec{p(t)} &= B_0^2(t)\vec{p_0} + B_1^2(t)\vec{p_1} + B_2^2(t)\vec{p_2} \\
&= (1-t)^2\vec{p_0} + 2t(1 - t)\vec{p_1} + t^2\vec{p_2},\quad (\vec{p_i}\in R^2)
\end{array}

ここで $\vec{p_i}$ は制御点です。また $B_i^2(t)$ は2次の Bernstein 基底関数と呼ばれるものなのですが、ここではそんなことはどうでも良くて、大事なのは $B_i^2(t)$ は $t$ の2次関数であるということです。2次関数であるということは、結局のところこのベジェ曲線は放物線であるということです。（細かいことを言えば3つの制御点が同一直線上に並んでいれば直線になりますが、そういうコーナーケースは目を瞑っておきましょう）

放物線をどう変形したところで、それは放物線であって円弧にはなりません。つまり制御点 $\vec{p_i}$ をどう動かしてもこのベジェ曲線を円弧にすることは出来ないわけです。ところが、これを有理ベジェ曲線というものに拡張すると円弧も表現できるようになるのです。そのカギは次の2つです。

• (A) 3D空間を2Dのスクリーンに透視投影（中心射影）すると、（ある条件の）円錐面は円弧に投影される。
• (B) 放物線は円錐曲線である。円錐面を母線に平行な平面で切断すると放物線となる。

まず(A)から説明します。下図のようにカメラで3D空間を撮影することを考えます。

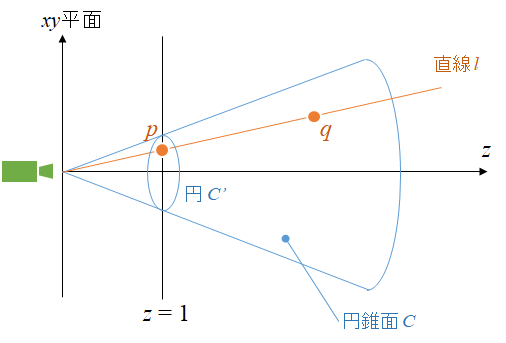
Z=1 の面に仮想的なスクリーンがあると考えましょう。このとき、視点から伸びる直線 $l$ はスクリーン上の1点 $p$ に投影されることが分かります。この延長で考えると、円錐面 $C$ はスクリーン上では円 $C'$ に投影されることが分かるかと思います。カメラでメガホンを上図のような姿勢で撮影すると円に見えるということですね。

このような射影変換を式で表しておきましょう。3D空間の点座標を $q=(\xi, \eta, \zeta)$、これをスクリーンに投影した2D座標を $p=(x, y)$ とすると、次式で表すことが出来ます。（Z座標で割り算するだけなので簡単ですね）

x = \frac{\xi}{\zeta},\quad y = \frac{\eta}{\zeta}

次に(B)です。下図のように円錐を母線に平行な平面で切断すると、その断面は放物線になります。（図は https://kotobank.jp/word/%E5%86%86%E9%8C%90%E6%9B%B2%E7%B7%9A-38198 より引用）

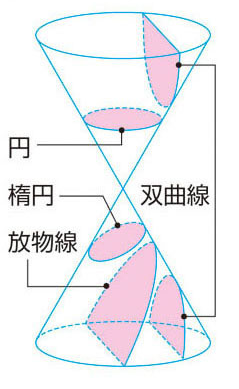
つまり、透視投影で図示した円錐面 $C$ も母線に平行に切断すれば放物線になります。そして、その放物線はベジェ曲線で表現することが出来ます。その放物線がスクリーンに投影された像は、そう、円弧です！

今思いついたのですが、針金を曲げて放物線を作って、それをカメラで撮影すると円弧に見える姿勢があるということになりますね。実際にやってみたら面白いかも？（そうでもないか…）

さて、まとめに入っていきます。2次元平面に円弧を描くためには、まず3次元空間にベジェ曲線で放物線を描いて、それを射影変換すれば良いということが分かりました。同様に3次元空間に円弧を描くためには、まず4次元空間（！）にベジェ曲線で放物線を描いて、それを射影変換することになります。このように、実際に作図したい空間よりも一つ高い次元の空間を考える必要が出てきます。このような一つ次元の高い座標を「同次座標」といいます。

制御点 $\vec{p_i} = (x_i, y_i)$ に重み $w_i$ を与えて、次のように同次座標 $\vec{q_i}$ を作ることにします。

\vec{q_i} = \left(\begin{array}{c}w_ix_i \\ w_iy_i \\ w_i \end{array}\right)

これを使って、同次座標系（3次元空間）にベジェ曲線を作ります。

\vec{q(t)} = B_0^2(t)\vec{q_0} + B_1^2(t)\vec{q_1} + B_2^2(t)\vec{q_2}

これを2次元平面に射影変換すると、それが有理ベジェ曲線となります。

\vec{p(t)} = \frac{w_0B_0^2(t)\vec{p_0} + w_1B_1^2(t)\vec{p_1} + w_2B_2^2(t)\vec{p_2}}{w_0B_0^2(t) + w_1B_1^2(t) + w_2B_2^2(t)}

多項式の分数式になっているので「有理（Rational）」という名前が付いているのだと思います。しかし個人的には、分数式であることを強調するよりも「射影曲線」とでも名付けたほうが上記の性質を表している気がするのですが、どうなんでしょうね。重み $w_i$ は決して円弧を表すためだけに使われるわけではないので、射影で捉えることだけを強調した名前にするのも良くないのかな。

NURBS まとめ

簡単にまとめておきます。NURBS曲線は、下記の種類の曲線を包含した、より自由度の高い曲線です。

• ベジェ曲線
• Bスプライン曲線
• 円錐曲線（円弧、楕円等）

同様にNURBS曲面というのもあり、ベジェ曲面やBスプライン曲面を包含しているのはもちろんのこと、有理式によって球面なども表現することが出来ます。

かように高い表現能力を持つNURBS曲線/曲面ですが、これによってどんなメリットがあるのでしょうか。
例として、曲線同士の交点計算を行うプログラムを作ることを考えてみましょう。曲線の種類（直線、円弧、楕円、放物線、ベジェ、…）が n 種類あったとすると、交点計算の組み合わせは n(n-1)/2 通りとなり、n が増えると非常に面倒で煩雑になります。しかしこれらがすべてNURBS曲線として表現できるのであれば、NURBS曲線同士の交点計算プログラムを1つ作るだけで済みます（ただし汎用的で信頼性があり高速なNURBSの交点計算プログラムを作るのはとても難しい…）。

しかし、かなり私の個人的な意見になりますが、メリットばかりではないようにも思えるのですよね…。まあその辺は恨み節（＝論理的に整理されていない愚痴）になるだけという部分も多いので、ここでは書かないでおきましょう。

さいごに

基礎となるメッシュと、3D CAD の形状表現について駆け足でざっと紹介しました。しかし形状を表現する方法はこれだけではありません。他にも様々な手法があるので、ここでは紹介できなかったトピックを簡単に箇条書きしてこの記事の終わりとします。

• 陰関数表現と等値面生成
• 計測点群
• Zマップとデクセル

※ もしこういったお仕事にご興味ありましたらご一報下さい(^^)