#二重振り子とは
https://www.youtube.com/watch?v=25feOUNQB2Y
カオス現象として有名な実験です。
カオス現象とは初期状態がその後の状態に大きく影響を与える現象です。
バタフライエフェクトという、蝶の羽が気流によって台風が発生するという話も同じカオス現象の説明で出てきます。(正しいくないかもしれません)
こちらで作ったオイラー・ラグランジュ法を用いて運動方程式の導出・シミュレーションをします。
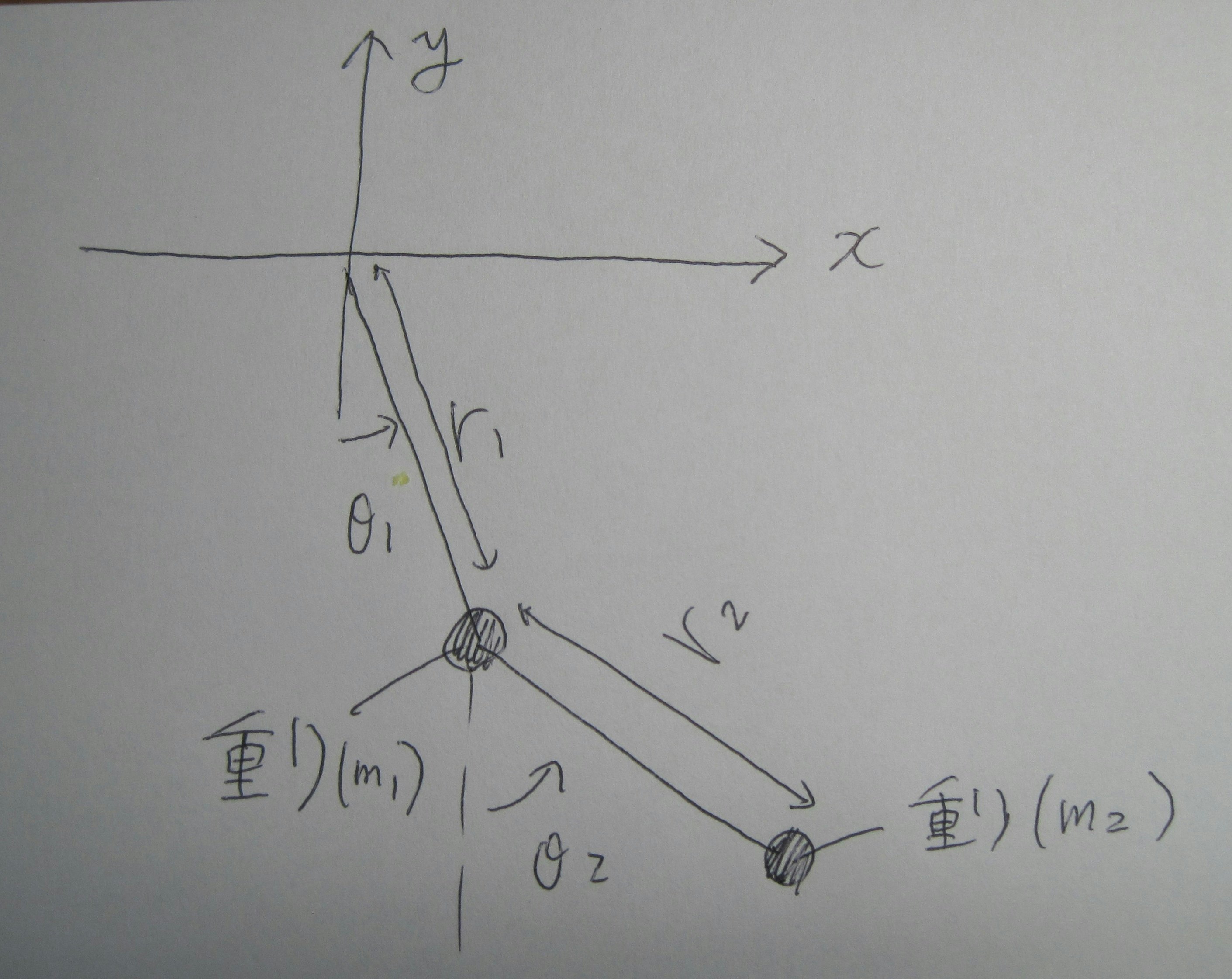
質点系・二次元で問題設定します。
m1の速度、m2の速度は
\vec{R_{m_1}} =\left(
\begin{array}{ccc}
r_1 sin(\theta_1) \\
-r_1 cos(\theta_1)
\end{array}
\right) ,
\vec{R_{m_2}}=\vec{R_{m_1}} +\left(
\begin{array}{ccc}
r_2 sin(\theta_1) \\
-r_2 cos(\theta_1)
\end{array}
\right) \\
\vec{V_{m_1}} =\left(
\begin{array}{ccc}
r_1 cos(\theta_1) \\
r_1 sin(\theta_1)
\end{array}
\right) \dot{\theta_1},
\vec{V_{m_2}}=\vec{V_{m_1}} +\left(
\begin{array}{ccc}
r_2 cos(\theta_1) \\
r_2 sin(\theta_1)
\end{array}
\right) \dot{\theta_2}\\
運動エネルギーTは
T=\frac{1}{2} m_1 |\vec{V_{m_1}}|^2+\frac{1}{2} m_2 |\vec{V_{m_2}}|^2
位置エネルギUは
U=m_1gr_1(1-cos(\theta_1)) + m_2g(r_1(1-cos(\theta_1)) + r_2(1-cos(\theta_2))
ラグランジアンを計算すると
L= m_1*r_1^2/2 + m2*r_2^2 /2 \dot{ x_1}^{2.0} +
m_2*r_2^2/2 \dot{ x_2}^{2.0} +
m_2*r_1*r_2 \dot{ x_1}^{1.0} sin( x_1)^{1.0} \dot{ x_2}^{1.0} sin( x_2)^{1.0} +
m_2*r_1*r_2 \dot{ x_1}^{1.0} cos( x_1)^{1.0} \dot{ x_2}^{1.0} cos( x_2)^{1.0} +
-1*(g*(m_1*r_1+m_2*(r_1+r_2))) +
-1*(-1*g*(m_1*r_1+m_2*r_1)) cos( x_1)^{1.0} +
-1*(-1*g*r_2*m_2) cos( x_2)^{1.0}
\\
\theta_1 = x_1\\
\theta_2 = x_2 とした
運動方程式を導出すると
(m_2*r_1*r_2*1.0) + -1*( ( (m_2*r_1*r_2*1.0) *1.0) ) \dot{ x_1}^{1.0} cos( x_1)^{1.0} \dot{ x_2}^{1.0} sin( x_2)^{1.0} +
(m_2*r_1*r_2*(-1)*1.0) + -1*( ( (m_2*r_1*r_2*1.0) *(-1)*1.0) ) \dot{ x_1}^{1.0} sin( x_1)^{1.0} \dot{ x_2}^{1.0} cos( x_2)^{1.0} +
(-1*(-1*g*(m_1*r_1+m_2*r_1))*(-1)*1.0) sin( x_1)^{1.0} +
-1*( ( (m_1*r_1^2/2 + m2*r_2^2 /2*2.0) *1.0) ) \ddot { x_1}^{1.0} +
-1*( ( (m_2*r_1*r_2*1.0) *1.0) ) sin( x_1)^{1.0} \dot{ x_2}^{2.0} cos( x_2)^{1.0} +
-1*( ( (m_2*r_1*r_2*1.0) *(-1)*1.0) ) cos( x_1)^{1.0} \dot{ x_2}^{2.0} sin( x_2)^{1.0} +
-1*( ( (m_2*r_1*r_2*1.0) *1.0) ) sin( x_1)^{1.0} \ddot { x_2}^{1.0} sin( x_2)^{1.0} +
-1*( ( (m_2*r_1*r_2*1.0) *1.0) ) cos( x_1)^{1.0} \ddot { x_2}^{1.0} cos( x_2)^{1.0} = 0 \\
(m_2*r_1*r_2*1.0) + -1*( ( (m_2*r_1*r_2*1.0) *1.0) ) \dot{ x_1}^{1.0} sin( x_1)^{1.0} \dot{ x_2}^{1.0} cos( x_2)^{1.0} +
(m_2*r_1*r_2*(-1)*1.0) + -1*( ( (m_2*r_1*r_2*1.0) *(-1)*1.0) ) \dot{ x_1}^{1.0} cos( x_1)^{1.0} \dot{ x_2}^{1.0} sin( x_2)^{1.0} +
(-1*(-1*g*r_2*m_2)*(-1)*1.0) sin( x_2)^{1.0} +
-1*( ( (m_2*r_1*r_2*1.0) *1.0) ) \dot{ x_1}^{2.0} cos( x_1)^{1.0} sin( x_2)^{1.0} +
-1*( ( (m_2*r_1*r_2*1.0) *(-1)*1.0) ) \dot{ x_1}^{2.0} sin( x_1)^{1.0} cos( x_2)^{1.0} +
-1*( ( (m_2*r_1*r_2*1.0) *1.0) ) \ddot { x_1}^{1.0} sin( x_1)^{1.0} sin( x_2)^{1.0} +
-1*( ( (m_2*r_1*r_2*1.0) *1.0) ) \ddot { x_1}^{1.0} cos( x_1)^{1.0} cos( x_2)^{1.0} +
-1*( ( (m_2*r_2^2/2*2.0) *1.0) ) \ddot { x_2}^{1.0} =0
使った、コードは見にくいので最後に添付します。
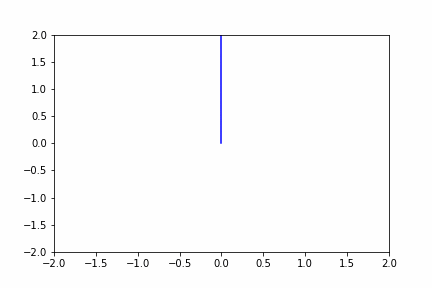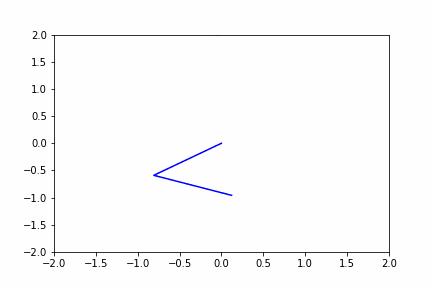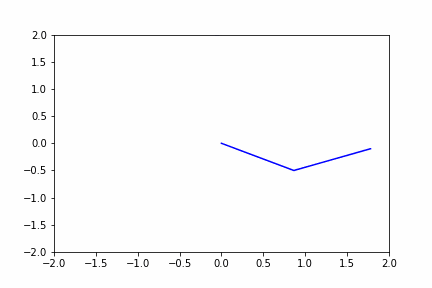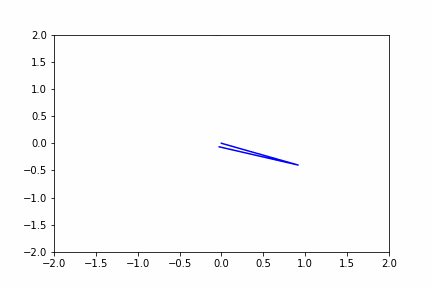
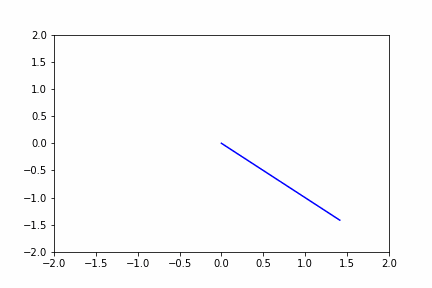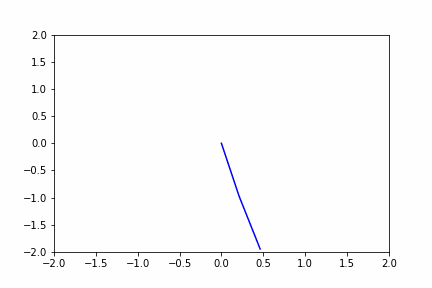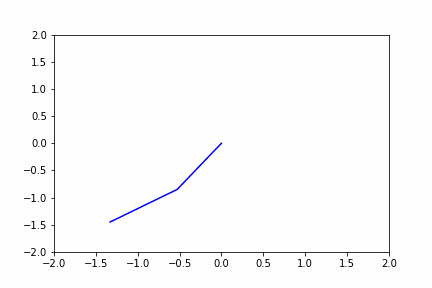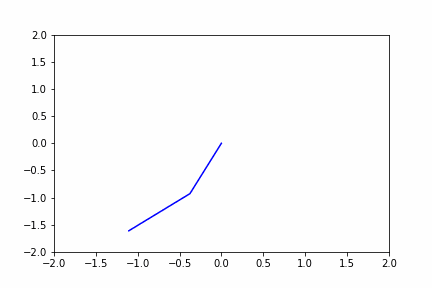
#シミュレーション(オイラー法)
得られた式を用いて、オイラー法でシミュレーションすると
設定
m1=1.0\\
m2=1.0\\
r1=1.0\\
r2=1.0\\
g=9.81\\
初期値:
\theta_1 = 180deg\\
\theta_2 = 180deg\\
\dot{\theta_1 }= 2rad/s\\
\dot{\theta_2} = 2rad/s\\
初期値:
\theta_1 = 180deg\\
\theta_2 = 180deg\\
\dot{\theta_1 }= 0.1rad/s\\
\dot{\theta_2} = 0.1rad/s
\theta_1 = 45deg\\
\theta_2 = 45deg\\
\dot{\theta_1 }= 0.1rad/s\\
\dot{\theta_2} = 0.1rad/s
#運動方程式導出コード
ここから先は、作ったプログラムになります。
コピペで動くはずです。
anaconda python2で実行しています。
gifアニメ化するためにこちら
https://qiita.com/yubais/items/c95ba9ff1b23dd33fde2
を参考にしました。
解析用クラス
import numpy as np # Numpyライブラリ
import copy
import math
'''
数式処理プログラム
列 : 多項式
行 : θ θ・ θ・・ sinθ cosθ 係数
の6個 × 変数数
文字式に対応させる
ただし、
'''
class Formula2 :
def __init__(self,L,num,coeff):
self.L = L
self.n = num #変数の種類数
self.coeff = coeff
#print self.coeff.dtype
def __add__(self,other):
self.L = np.append(self.L,other.L,axis =0)
#print self.coeff.dtype
#print other.coeff.dtype
expr,vari = self.L.shape
self.coeff = np.append(self.coeff,other.coeff,axis =0)
self.together()
#self.erase()
def __sub__(self,other):
expr,vari = other.L.shape
hoge = copy.deepcopy(other.L)
for i in range(expr):
hoge[i][5] = hoge[i][5] * -1
self.L = np.append(self.L,hoge,axis =0)
for i in range(expr):
other.coeff[i] = "-1*(" + other.coeff[i] +")"
self.coeff = np.append(self.coeff,other.coeff,axis =0)
self.together()
#self.erase()
def together(self): #同じ項の係数をまとめる
expr,vari = self.L.shape
if expr >=2:
for i in range(expr-1):
for j in range(i+1,expr):
m=0
while self.L[i][0+m*6:5+m*6].tolist() == self.L[j][0+m*6:5+m*6].tolist():
m += 1
if m == self.n:
break
if m== self.n: #全部一致 係数の足し算
self.L[i][5] += self.L[j][5]
self.coeff[i] = self.coeff[i] +" + "+ self.coeff[j]
for k in range(vari): # j 行削除
self.L[j][k] = 0
self.coeff[j] = "0"
def erase(self): #係数が0の項を消す
expr,vari = self.L.shape
for i in list(reversed(range(expr))):
if self.coeff[i] == "0":
self.L = np.delete(self.L,i,axis = 0)
self.coeff =np.delete(self.coeff,i,axis = 0)
def partial(self,moji,kind): #kindの種類のもので項を偏微分する
expr,vari = self.L.shape
if kind == 0:
'''
sin
cos
+moji*6
'''
#print self.L
for i in range(expr):
if self.L[i][3+moji*6] !=0: #sin
hoge = copy.deepcopy(self.L[i])
hogestr = copy.deepcopy(self.coeff[i])
hoge[5] = hoge[5]*hoge[3+moji*6]
#係数に hoge[3+moji*6]を かける
hogestr = " ("+hogestr+"*"+str(hoge[3+moji*6])+") "
hoge[3+moji*6] = hoge[3+moji*6]-1
hoge[4+moji*6] = hoge[4+moji*6]+1
self.L = np.append(self.L,hoge[np.newaxis,:],axis =0)
self.coeff = np.append(self.coeff,[hogestr],axis =0)
#print self.L
for i in range(expr):
if self.L[i][4+moji*6] !=0: #cos
hoge = copy.deepcopy(self.L[i])
hogestr = copy.deepcopy(self.coeff[i])
hoge[5] = hoge[5]*hoge[4+moji*6]*-1
#係数に hoge[3+moji*6]を かける
hogestr = " ("+hogestr+"*(-1)*"+str(hoge[4+moji*6])+") "
hoge[4+moji*6]= hoge[4+moji*6]-1
hoge[3+moji*6] = hoge[3+moji*6]+1
self.L = np.append(self.L,hoge[np.newaxis,:],axis =0)
self.coeff = np.append(self.coeff,[hogestr],axis =0)
#print self.L
'''
そのままのもの
次数を一つ下げる、0なら何もしない
元の次数を係数に掛ける
sin,cos処理部は後ろにあって処理範囲にないため大丈夫
'''
for i in range(expr):
if self.L[i][kind] !=0:
#print kind,self.L[i][5]
self.L[i][5] = self.L[i][5] * self.L[i][kind+moji*6]
self.coeff[i] = " ("+self.coeff[i]+"*"+str(self.L[i][kind+moji*6])+") "
#print self.L[i][5]
self.L[i][kind+moji*6] = self.L[i][kind+moji*6] -1
else:
self.L[i][5] = 0 #含まないなら 0
self.coeff[i] = "0"
if kind == 1:
'''
そのままのもの
次数を一つ下げる、0なら何もしない
元の次数を係数に掛ける
'''
for i in range(expr):
if self.L[i][kind+moji*6] !=0:
self.L[i][5] = self.L[i][5] * self.L[i][kind+moji*6]
self.coeff[i] = " ("+self.coeff[i]+"*"+str(self.L[i][kind+moji*6])+") "
self.L[i][kind+moji*6] = self.L[i][kind+moji*6] -1
else:
self.L[i][5] = 0 #含まないなら 0
self.coeff[i] = "0"
self.together()
self.erase()
def diff(self): #時間微分
'''
4つのパターンで偏微分後
θ・の次数を1上げる
'''
L1=copy.deepcopy(self.L)
L1_coeff = copy.deepcopy(self.coeff)
for i in range(self.n):
self.L =copy.deepcopy( L1) #L1:微分前 L2:結果保存用
self.coeff = copy.deepcopy(L1_coeff)
self.partial(i,0)
expr,vari = self.L.shape
#print expr
#print self.L
for j in range(expr):
self.L[j][1+i*6] = self.L[j][1+i*6] + 1
if i == 0:
L2 = copy.deepcopy( self.L)
L2_coeff = copy.deepcopy(self.coeff)
else:
L2 = np.append(L2,self.L,axis =0)
L2_coeff = np.append(L2_coeff,self.coeff,axis =0)
self.L =copy.deepcopy( L1)
self.coeff = copy.deepcopy(L1_coeff)
self.partial(i,1)
expr,vari = self.L.shape
for j in range(expr):
self.L[j][2+i*6] += 1
L2 = np.append(L2,self.L,axis =0)
L2_coeff = np.append(L2_coeff,self.coeff,axis =0)
self.L = copy.deepcopy( L2)
self.coeff = copy.deepcopy(L2_coeff)
self.together()
self.erase()
def disp2(self): #多項式表示
print "-------------------Formula--------------"
expr,vari = self.L.shape
for j in range(expr):
hoge =""
for i in range(self.n):
hoge += "["+str(i+1)+" "
if i == 0:
hoge += self.coeff[j]+" "
if self.L[j][0+i*6]!= 0:
hoge += " θ^"
hoge += str(self.L[j][0+i*6])
if self.L[j][1+i*6]!= 0:
hoge += " θ・^"
hoge += str(self.L[j][1+i*6])
if self.L[j][2+i*6]!= 0:
hoge += " θ・・^"
hoge += str(self.L[j][2+i*6])
if self.L[j][3+i*6]!= 0:
hoge += " sin^"
hoge += str(self.L[j][3+i*6])
if self.L[j][4+i*6]!= 0:
hoge += " cos^"
hoge += str(self.L[j][4+i*6])
hoge += " ] "
hoge += " + "
print hoge
#print self.coeff
def latex(self):
variable = " x"
k=1
print "-------------------Formula_latex---------"
expr,vari = self.L.shape
for j in range(expr):
hoge =""
for i in range(self.n):
hoge += " "
if i == 0:
hoge += self.coeff[j]
if self.L[j][0+i*6]!= 0:
hoge += variable+"_"+str(i+k)+"^{"
hoge += str(self.L[j][0+i*6])+"}"
if self.L[j][1+i*6]!= 0:
hoge += " \dot{"+variable+"_"+str(i+k)+"}^{"
hoge += str(self.L[j][1+i*6])+"}"
if self.L[j][2+i*6]!= 0:
hoge += " \ddot {"+variable+"_"+str(i+k)+"}^{"
hoge += str(self.L[j][2+i*6])+"}"
if self.L[j][3+i*6]!= 0:
hoge += " sin("+variable+"_"+str(i+k)+")^{"
hoge += str(self.L[j][3+i*6])+"}"
if self.L[j][4+i*6]!= 0:
hoge += " cos("+variable+"_"+str(i+k)+")^{"
hoge += str(self.L[j][4+i*6])+"}"
hoge += " "
hoge += " + "
print hoge
def separete(self): #2変数と考えて、 1 2 b の3つに分割する
a1=np.asarray([[]])
a2=np.asarray([[]])
coeff1 = np.asarray([],dtype = object)
coeff2 = np.asarray([],dtype = object)
expr,vari = self.L.shape
for j in range(expr)[::-1]:
if self.L[j][2] == 1:
if len(a1[0]) == 0:
a1=(self.L[j]) [np.newaxis,:]
coeff1=np.asarray([self.coeff[j]],dtype = object)
else:
a1 = np.append(a1,(self.L[j]) [np.newaxis,:],axis =0)
coeff1=np.append(coeff1,[self.coeff[j]],axis = 0)
self.L = np.delete(self.L,j,0)
self.coeff=np.delete(self.coeff,j,0)
continue
if self.L[j][8] == 1:
if len(a2[0]) == 0:
a2=(self.L[j]) [np.newaxis,:]
coeff2=np.asarray([self.coeff[j]],dtype = object)
else:
a2 = np.append(a2,(self.L[j]) [np.newaxis,:],axis =0)
coeff2=np.append(coeff2,[self.coeff[j]],axis = 0)
self.L = np.delete(self.L,j,0)
self.coeff=np.delete(self.coeff,j,0)
continue
if len(a1[0]) == 0:
a1 =np.asarray([ [0,0,0,0,0,0 ,0,0,0,0,0,0]])
coeff1 = np.asarray(["0"],dtype = object)
if len(a2[0]) == 0:
a2 = np.asarray([[0,0,0,0,0,0 ,0,0,0,0,0,0]])
coeff2 = np.asarray(["0"],dtype = object)
L1 = Formula2(a1,2,coeff1)
L2 = Formula2(a2,2,coeff2)
return L1,L2
def separete3(self): #3変数と考えて、 1 2 3 b の 4 つに分割する
a1=np.asarray([[]])
a2=np.asarray([[]])
a3=np.asarray([[]])
coeff1 = np.asarray([],dtype = object)
coeff2 = np.asarray([],dtype = object)
coeff3 = np.asarray([],dtype = object)
expr,vari = self.L.shape
for j in range(expr)[::-1]:
if self.L[j][2] == 1:
if len(a1[0]) == 0:
a1=(self.L[j]) [np.newaxis,:]
coeff1=np.asarray([self.coeff[j]],dtype = object)
else:
a1 = np.append(a1,(self.L[j]) [np.newaxis,:],axis =0)
coeff1=np.append(coeff1,[self.coeff[j]],axis = 0)
self.L = np.delete(self.L,j,0)
self.coeff=np.delete(self.coeff,j,0)
continue
if self.L[j][8] == 1:
if len(a2[0]) == 0:
a2=(self.L[j]) [np.newaxis,:]
coeff2=np.asarray([self.coeff[j]],dtype = object)
else:
a2 = np.append(a2,(self.L[j]) [np.newaxis,:],axis =0)
coeff2=np.append(coeff2,[self.coeff[j]],axis = 0)
self.L = np.delete(self.L,j,0)
self.coeff=np.delete(self.coeff,j,0)
continue
if self.L[j][14] == 1:
if len(a3[0]) == 0:
a3=(self.L[j]) [np.newaxis,:]
coeff3=np.asarray([self.coeff[j]],dtype = object)
else:
a3 = np.append(a3,(self.L[j]) [np.newaxis,:],axis =0)
coeff3=np.append(coeff3,[self.coeff[j]],axis = 0)
self.L = np.delete(self.L,j,0)
self.coeff=np.delete(self.coeff,j,0)
continue
if len(a1[0]) == 0:
a1 =np.asarray([ [0,0,0,0,0,0 ,0,0,0,0,0,0 ,0,0,0,0,0,0]])
coeff1 = np.asarray(["0"],dtype = object)
if len(a2[0]) == 0:
a2 = np.asarray([[0,0,0,0,0,0 ,0,0,0,0,0,0 ,0,0,0,0,0,0]])
coeff2 = np.asarray(["0"],dtype = object)
if len(a3[0]) == 0:
a3 = np.asarray([[0,0,0,0,0,0 ,0,0,0,0,0,0 ,0,0,0,0,0,0]])
coeff3 = np.asarray(["0"],dtype = object)
L1 = Formula2(a1,3,coeff1)
L2 = Formula2(a2,3,coeff2)
L3 = Formula2(a3,3,coeff3)
return L1,L2,L3
if __name__ == '__main__':
print "This is not for main TEST RESULT"
T=np.asarray([[1,2,0,4,5,1 ,1,2,0,4,5,1]])
coeff = np.asarray(["m "], dtype=object)
print coeff.dtype
sai =Formula2(T,2,coeff)
sai.disp2()
sai.diff()
sai.disp2()
#sai.latex()
L1,L2= sai.separete()
L1.disp2()
'''
L1+L2
L1.disp2()
'''
実行コード
import numpy as np # Numpyライブラリ
import copy
import math
#import matplotlib.pyplot as plt
import matplotlib
#matplotlib.use('Agg') # -----(1)
import matplotlib.pyplot as plt
import matplotlib.animation as animation
from matplotlib.animation import PillowWriter
import Formula2
#L= np.asarray([[7,2,3,4,5,6, 7,2,3,4,5,6]])
#L= np.asarray([[2,2,0,5,4,5],[2,2,0,5,4,5]])
'''
L1,L2 の二つしか 式がなく、変数も2つの場合で考えよう
式 ≒ 0 として、
θ・・の項のみ取り出し新しいインスタンス化
除かれた方をbとして[L1_b,L2_b]ベクトルを作る
θ・・の項は
[L1_1 L1_2
L2_1 L2_2 ] というインスタンスの行列 A を考える
L1_2 = L1の式の中の θ2・・の項
θ・・ = A^-1 b を計算
オイラー法の陽解法でθ・ θ も出てくる
ここまでやってみよう
L1_b,L1_1,L1_2 を生成する 方法を考える
'''
m1=1.0
m2=1.0
r1=1.0
r2=1.0
g=9.81
T=np.asarray([[0,2,0,0,0,m1*r1**2/2 + m2*r2**2 /2,
0,0,0,0,0,1],
[0,0,0,0,0,m2*r2**2/2 ,
0,2,0,0,0,1],
[0,1,0,1,0,m2*r1*r2,
0,1,0,1,0,1],
[0,1,0,0,1,m2*r1*r2,
0,1,0,0,1,1]]
)
T_n=np.asarray(["m_1*r_1^2/2 + m2*r_2^2 /2",
"m_2*r_2^2/2" ,
"m_2*r_1*r_2",
"m_2*r_1*r_2"],dtype=object )
U= np.asarray([[0,0,0,0,0,g*(m1*r1+m2*(r1+r2)),
0,0,0,0,0,1],
[0,0,0,0,1,-1*g*(m1*r1+m2*r1),
0,0,0,0,0,1],
[0,0,0,0,0,-1*g*r2*m2,
0,0,0,0,1,1]
])
U_n= np.asarray(["g*(m_1*r_1+m_2*(r_1+r_2))",
"-1*g*(m_1*r_1+m_2*r_1)",
"-1*g*r_2*m_2"],dtype=object)
T1=Formula2.Formula2(T,2,T_n)
SaveT = copy.deepcopy(T1)
U1=Formula2.Formula2(U,2,U_n)
T1-U1
Lt_1=copy.deepcopy(T1)
Lt_2=copy.deepcopy(T1)
Lt_1.partial(0,0)
Lt_2.partial(0,1)
Lt_2.diff()
Lt_1-Lt_2
Ls_1=copy.deepcopy(T1)
Ls_2=copy.deepcopy(T1)
Ls_1.partial(1,0)
Ls_2.partial(1,1)
Ls_2.diff()
Ls_1-Ls_2
Lt_1.disp2()
Ls_1.disp2()
T1.disp2()
L1 = copy.deepcopy(Ls_1)
L2 = copy.deepcopy(Lt_1)
L1_1,L1_2 = L1.separete()
L2_1,L2_2 = L2.separete()
'''
T1:ラグランジアン
Lt_1 ,L1 :θ1に関する運動方程式
Ls_2 ,L2 :θ2に関する運動方程式
'''
#シミュレーションコード
解析用クラス
import numpy as np # Numpyライブラリ
import copy
import math
'''
数式処理プログラム
列 : 多項式
行 : θ θ・ θ・・ sinθ cosθ 係数
の6個 × 変数数
'''
class Formula :
def __init__(self,L,num):
self.L = L
self.n = num #変数の種類数
def __add__(self,other):
self.L = np.append(self.L,other.L,axis =0)
self.together()
self.erase()
def __sub__(self,other):
expr,vari = other.L.shape
hoge = copy.deepcopy(other.L)
for i in range(expr):
hoge[i][5] = hoge[i][5] * -1
self.L = np.append(self.L,hoge,axis =0)
self.together()
self.erase()
def latex(self):
variable = " x"
k=1
print "-------------------Formula--------------"
expr,vari = self.L.shape
for j in range(expr):
hoge =""
for i in range(self.n):
hoge += " "
if self.L[j][5]!= 0:
if i == 0:
hoge += str(self.L[j][5+i*6])
if self.L[j][0+i*6]!= 0:
hoge += variable+"_"+str(i+k)+"^{"
hoge += str(self.L[j][0+i*6])+"}"
if self.L[j][1+i*6]!= 0:
hoge += " \dot{"+variable+"_"+str(i+k)+"}^{"
hoge += str(self.L[j][1+i*6])+"}"
if self.L[j][2+i*6]!= 0:
hoge += " \ddot {"+variable+"_"+str(i+k)+"}^{"
hoge += str(self.L[j][2+i*6])+"}"
if self.L[j][3+i*6]!= 0:
hoge += " sin("+variable+"_"+str(i+k)+")^{"
hoge += str(self.L[j][3+i*6])+"}"
if self.L[j][4+i*6]!= 0:
hoge += " cos("+variable+"_"+str(i+k)+")^{"
hoge += str(self.L[j][4+i*6])+"}"
hoge += " "
hoge += " + "
print hoge
def together(self): #同じ項の係数をまとめる
expr,vari = self.L.shape
if expr >=2:
for i in range(expr-1):
for j in range(i+1,expr):
m=0
while self.L[i][0+m*6:5+m*6].tolist() == self.L[j][0+m*6:5+m*6].tolist():
m += 1
if m == self.n:
break
if m== self.n:
self.L[i][5] += self.L[j][5]
for k in range(vari):
self.L[j][k] = 0
def erase(self): #係数が0の項を消す
expr,vari = self.L.shape
for i in list(reversed(range(expr))):
if self.L[i][5] == 0:
self.L = np.delete(self.L,i,axis = 0)
def partial(self,moji,kind): #kindの種類のもので項を偏微分する
expr,vari = self.L.shape
if kind == 0:
'''
sin
cos
+moji*6
'''
#print self.L
for i in range(expr):
if self.L[i][3+moji*6] !=0: #sin
hoge = copy.deepcopy(self.L[i])
hoge[5] = hoge[5]*hoge[3+moji*6]
hoge[3+moji*6] = hoge[3+moji*6]-1
hoge[4+moji*6] = hoge[4+moji*6]+1
self.L = np.append(self.L,hoge[np.newaxis,:],axis =0)
#print self.L
for i in range(expr):
if self.L[i][4+moji*6] !=0: #cos
hoge = copy.deepcopy(self.L[i])
hoge[5] = hoge[5]*hoge[4+moji*6]*-1
hoge[4+moji*6]= hoge[4+moji*6]-1
hoge[3+moji*6] = hoge[3+moji*6]+1
self.L = np.append(self.L,hoge[np.newaxis,:],axis =0)
#print self.L
'''
そのままのもの
次数を一つ下げる、0なら何もしない
元の次数を係数に掛ける
'''
#print self.L
for i in range(expr):
if self.L[i][kind] !=0:
#print kind,self.L[i][5]
self.L[i][5] = self.L[i][5] * self.L[i][kind+moji*6]
#print self.L[i][5]
self.L[i][kind+moji*6] = self.L[i][kind+moji*6] -1
else:
self.L[i][5] = 0 #含まないなら 0
if kind == 1:
'''
そのままのもの
次数を一つ下げる、0なら何もしない
元の次数を係数に掛ける
'''
for i in range(expr):
if self.L[i][kind+moji*6] !=0:
self.L[i][5] = self.L[i][5] * self.L[i][kind+moji*6]
self.L[i][kind+moji*6] = self.L[i][kind+moji*6] -1
else:
self.L[i][5] = 0 #含まないなら 0
self.together()
self.erase()
def diff(self): #時間微分
'''
4つのパターンで偏微分後
θ・の次数を1上げる
'''
L1=copy.deepcopy(self.L)
for i in range(self.n):
self.L =copy.deepcopy( L1)
self.partial(i,0)
expr,vari = self.L.shape
#print expr
#print self.L
for j in range(expr):
self.L[j][1+i*6] = self.L[j][1+i*6] + 1
if i == 0:
L2 = copy.deepcopy( self.L)
else:
L2 = np.append(L2,self.L,axis =0)
self.L =copy.deepcopy( L1)
self.partial(i,1)
expr,vari = self.L.shape
for j in range(expr):
self.L[j][2+i*6] += 1
L2 = np.append(L2,self.L,axis =0)
self.L = copy.deepcopy( L2)
self.together()
self.erase()
def disp(self): #多項式表示
print "-------------------Formula--------------"
expr,vari = self.L.shape
for j in range(expr):
hoge =""
for i in range(self.n):
hoge += str(self.L[j][5+i*6])
hoge += " θ^"
hoge += str(self.L[j][0+i*6])
hoge += " θ・^"
hoge += str(self.L[j][1+i*6])
hoge += " θ・・^"
hoge += str(self.L[j][2+i*6])
hoge += " sin^"
hoge += str(self.L[j][3+i*6])
hoge += " cos^"
hoge += str(self.L[j][4+i*6])
hoge += " "
hoge += " + "
print hoge
def disp2(self): #多項式表示
print "-------------------Formula--------------"
expr,vari = self.L.shape
for j in range(expr):
hoge =""
for i in range(self.n):
hoge += "["+str(i+1)+" "
if self.L[j][5]!= 0:
if i == 0:
hoge += str(self.L[j][5+i*6])
if self.L[j][0+i*6]!= 0:
hoge += " θ^"
hoge += str(self.L[j][0+i*6])
if self.L[j][1+i*6]!= 0:
hoge += " θ・^"
hoge += str(self.L[j][1+i*6])
if self.L[j][2+i*6]!= 0:
hoge += " θ・・^"
hoge += str(self.L[j][2+i*6])
if self.L[j][3+i*6]!= 0:
hoge += " sin^"
hoge += str(self.L[j][3+i*6])
if self.L[j][4+i*6]!= 0:
hoge += " cos^"
hoge += str(self.L[j][4+i*6])
hoge += " ] "
hoge += " + "
print hoge
def subst(self,x): #代入 x ,x・の順に入れる
vari =np.array(x).shape
if vari[0] != self.n*2:
print "cannot subst"
else:
'''
行ベクトルを生成して
dotでLと をして、できたベクトルの全要素を足せばよい
'''
expr,vari = self.L.shape
sum1 = 0
hoge=0
for j in range(expr):
hoge=self.L[j][5] #係数
for i in range(self.n):
hoge = hoge*x[0+i*2]**self.L[j][0+i*6] #θ
hoge = hoge*x[1+i*2]**self.L[j][1+i*6] #θ・
hoge = hoge*math.sin(x[0+i*2])**self.L[j][3+i*6] #sin
hoge = hoge*math.cos(x[0+i*2])**self.L[j][4+i*6] #cos
sum1 += hoge
return sum1
def separete(self): #2変数と考えて、 1 2 b の3つに分割する
a1=np.asarray([[]])
a2=np.asarray([[]])
expr,vari = self.L.shape
for j in range(expr)[::-1]:
if self.L[j][2] == 1:
if len(a1[0]) == 0:
a1=(self.L[j]) [np.newaxis,:]
else:
a1 = np.append(a1,(self.L[j]) [np.newaxis,:],axis =0)
self.L = np.delete(self.L,j,0)
continue
if self.L[j][8] == 1:
if len(a2[0]) == 0:
a2=(self.L[j]) [np.newaxis,:]
else:
a2 = np.append(a2,(self.L[j]) [np.newaxis,:],axis =0)
self.L = np.delete(self.L,j,0)
continue
if len(a1[0]) == 0:
a1 =np.asarray([ [0,0,0,0,0,0 ,0,0,0,0,0,0]])
if len(a2[0]) == 0:
a2 = np.asarray([[0,0,0,0,0,0 ,0,0,0,0,0,0]])
L1 = Formula(a1,2)
L2 = Formula(a2,2)
return L1,L2
def separete3(self): #3変数と考えて、 1 2 3 b の 4 つに分割する
a1=np.asarray([[]])
a2=np.asarray([[]])
a3=np.asarray([[]])
expr,vari = self.L.shape
for j in range(expr)[::-1]:
print "a1"
print a1.shape
print "a3"
print a3.shape
print "a2"
print a2.shape
if self.L[j][2] == 1:
if len(a1[0]) == 0:
a1=(self.L[j]) [np.newaxis,:]
else:
a1 = np.append(a1,(self.L[j]) [np.newaxis,:],axis =0)
self.L = np.delete(self.L,j,0)
continue
if self.L[j][8] == 1:
if len(a2[0]) == 0:
a2=(self.L[j]) [np.newaxis,:]
else:
a2 = np.append(a2,(self.L[j]) [np.newaxis,:],axis =0)
self.L = np.delete(self.L,j,0)
continue
if self.L[j][14] == 1:
if len(a3[0]) == 0:
a3=(self.L[j]) [np.newaxis,:]
else:
a3 = np.append(a3,(self.L[j]) [np.newaxis,:],axis =0)
self.L = np.delete(self.L,j,0)
continue
if len(a1[0]) == 0:
a1 =np.asarray([ [0,0,0,0,0,0 ,0,0,0,0,0,0 ,0,0,0,0,0,0]])
if len(a2[0]) == 0:
a2 = np.asarray([[0,0,0,0,0,0 ,0,0,0,0,0,0 ,0,0,0,0,0,0]])
if len(a3[0]) == 0:
a3 = np.asarray([[0,0,0,0,0,0 ,0,0,0,0,0,0 ,0,0,0,0,0,0]])
L1 = Formula(a1,3)
L2 = Formula(a2,3)
L3 = Formula(a3,3)
return L1,L2,L3
if __name__ == '__main__':
print "This is not for main"
実行プログラム
# -*- coding: utf-8 -*-
"""
Created on Sat Mar 21 14:11:03 2020
@author: kisim
"""
import numpy as np # Numpyライブラリ
import copy
import math
#import matplotlib.pyplot as plt
import matplotlib
#matplotlib.use('Agg') # -----(1)
import matplotlib.pyplot as plt
import matplotlib.animation as animation
from matplotlib.animation import PillowWriter
import Formula
#L= np.asarray([[7,2,3,4,5,6, 7,2,3,4,5,6]])
#L= np.asarray([[2,2,0,5,4,5],[2,2,0,5,4,5]])
'''
L1,L2 の二つしか 式がなく、変数も2つの場合で考えよう
式 ≒ 0 として、
θ・・の項のみ取り出し新しいインスタンス化
除かれた方をbとして[L1_b,L2_b]ベクトルを作る
θ・・の項は
[L1_1 L1_2
L2_1 L2_2 ] というインスタンスの行列 A を考える
L1_2 = L1の式の中の θ2・・の項
θ・・ = A^-1 b を計算
オイラー法の陽解法でθ・ θ も出てくる
ここまでやってみよう
L1_b,L1_1,L1_2 を生成する 方法を考える
'''
m1=1.0
m2=1.0
l1=1.0
l2=1.0
r1=1.0
r2=1.0
R1=1.0
g=9.81
T=np.asarray([[0,2,0,0,0,m1*r1**2/2 + m2*r2**2 /2,
0,0,0,0,0,1],
[0,0,0,0,0,m2*r2**2/2 ,
0,2,0,0,0,1],
[0,1,0,1,0,m2*r1*r2,
0,1,0,1,0,1],
[0,1,0,0,1,m2*r1*r2,
0,1,0,0,1,1]]
)
T_n=np.asarray(["m_1*r_1^2/2 + m2*r_2^2 /2",
"m_2*r_2^2/2" ,
"m_2*r_1*r_2",
"m_2*r_1*r_2"],dtype=object )
U= np.asarray([[0,0,0,0,0,g*(m1*r1+m2*(r1+r2)),
0,0,0,0,0,1],
[0,0,0,0,1,-1*g*(m1*r1+m2*r1),
0,0,0,0,0,1],
[0,0,0,0,0,-1*g*r2*m2,
0,0,0,0,1,1]
])
U_n= np.asarray(["g*(m_1*r_1+m_2*(r_1+r_2))",
"-1*g*(m_1*r_1+m_2*r_1)",
"-1*g*r_2*m_2"],dtype=object)
T1=Formula.Formula(T,2)
U1=Formula.Formula(U,2)
T1-U1
Lt_1=copy.deepcopy(T1)
Lt_2=copy.deepcopy(T1)
Lt_1.partial(0,0)
Lt_2.partial(0,1)
Lt_2.diff()
Lt_1-Lt_2
Ls_1=copy.deepcopy(T1)
Ls_2=copy.deepcopy(T1)
Ls_1.partial(1,0)
Ls_2.partial(1,1)
Ls_2.diff()
Ls_1-Ls_2
Lt_1.disp2()
Ls_1.disp2()
T1.disp2()
L1 = copy.deepcopy(Ls_1)
L2 = copy.deepcopy(Lt_1)
L1_1,L1_2 = L1.separete()
L2_1,L2_2 = L2.separete()
'''
Lt_1 :θ1に関する運動方程式
Ls_2 :θ2に関する運動方程式
'''
'''
オイラー法による数値解法を行う
初期値設定
解法
表示
の3プロセスを実装する必要がある
'''
DT = 0.001 #時刻
x=[math.pi,2,math.pi,2] #初期値
saveX = x
T=10
N=int(T/DT) #計算時間/DT
for i in range(N):
b1 = L1.subst(x) * -1
b2 = L2.subst(x) * -1
a11 = L1_1.subst(x)
a12 = L1_2.subst(x)
a21 = L2_1.subst(x)
a22 = L2_2.subst(x)
hoge = a11*a22-a12*a21
if hoge == 0:
print "hoge = 0 break"
break
alpha1 = (a22*b1-a12*b2)/hoge #A^-1 b
alpha2 = (a11*b2-a21*b1)/hoge
x2 =np.array( x ) + np.array( [ x[1] ,alpha1 ,x[3],alpha2 ] ) * DT
x = x2
saveX = np.append(saveX,x, axis=0)
saveX = saveX.reshape([4,N+1],order ='F')
t=[float(i)*DT for i in range(N+1)]
t= np.asarray(t)
'''
#点履歴
position_x1=r1*np.sin(saveX[0])
position_y1=-1*r1*np.cos(saveX[0])
position_x2=R1*np.sin(saveX[0])+r2*np.sin(saveX[2])
position_y2=-1*R1*np.cos(saveX[0]) - r2*np.cos(saveX[2])
plt.figure(figsize=(28, 20)) # (width, height)
plt.rcParams["font.size"] = 25
plt.plot(position_x1,position_y1,label ="1")
plt.plot(position_x2,position_y2,label="2")
plt.legend(fontsize = 25)
plt.savefig('figure0.png')
'''
'''
#グラフ化
z=np.sin(saveX[0])*R1+np.sin(saveX[2])*r2
plt.figure(figsize=(28, 20)) # (width, height)
plt.rcParams["font.size"] = 25
plt.plot(t,z,label ="z")
plt.plot(t,saveX[0],label="x0")
plt.plot(t,saveX[1],label="dt x0")
plt.plot(t,saveX[2],label="x1")
plt.plot(t,saveX[3],label="dt x1")
plt.legend(fontsize = 25)
plt.savefig('figure0.png')
'''
#animation化
print "start animation"
ims = []
fig,ax = plt.subplots()
ax.set_xlim([-2, 2])
ax.set_ylim([-2, 2])
Step = 100 #飛ばすフレーム数
for i in range(int(N/Step)):
position_x1=r1*np.sin(saveX[0][i*Step])
position_y1=-1*r1*np.cos(saveX[0][i*Step])
position_x2=R1*np.sin(saveX[0][i*Step])+r2*np.sin(saveX[2][i*Step])
position_y2=-1*R1*np.cos(saveX[0][i*Step]) - r2*np.cos(saveX[2][i*Step])
im = plt.plot([0,position_x1,position_x2],[0,position_y1,position_y2],color='blue') # 乱数をグラフにする
ims.append(im) # グラフを配列 ims に追加
# 10枚のプロットを 100ms ごとに表示
ani = animation.ArtistAnimation(fig, ims, interval=DT*Step)
ani.save("output2.gif", writer='pillow')