目的と概要
オイラー・ラグランジュ方程式による、運動方程式の導出はエネルギーを利用しているため、計算ミスが小さいという特徴があります。
3次元という複雑化する運動方程式でも適用が簡単であり、便利な方法です。
しかし、ラグランジアンを導出後の偏微分の計算、連立方程式の解法、というめんどくささがあります。
今回、投稿する内容は、ラグランジアン導入後、偏微分、時間微分をさせて、オイラー法を用いてシミュレーションするという内容です。
文字式にはまだ対応させていません。
また、sin,cos,d/dt^2/dt^2の多項式にしか対応させていません。
matlabやscilabを使える人は、全く関係ない話なのでブラウザバック推奨です。
3次元のY字振り子
https://www.youtube.com/watch?v=eeizdZscRjU
https://www.youtube.com/watch?v=llBik9FsEDo
をシミュレーションした結果は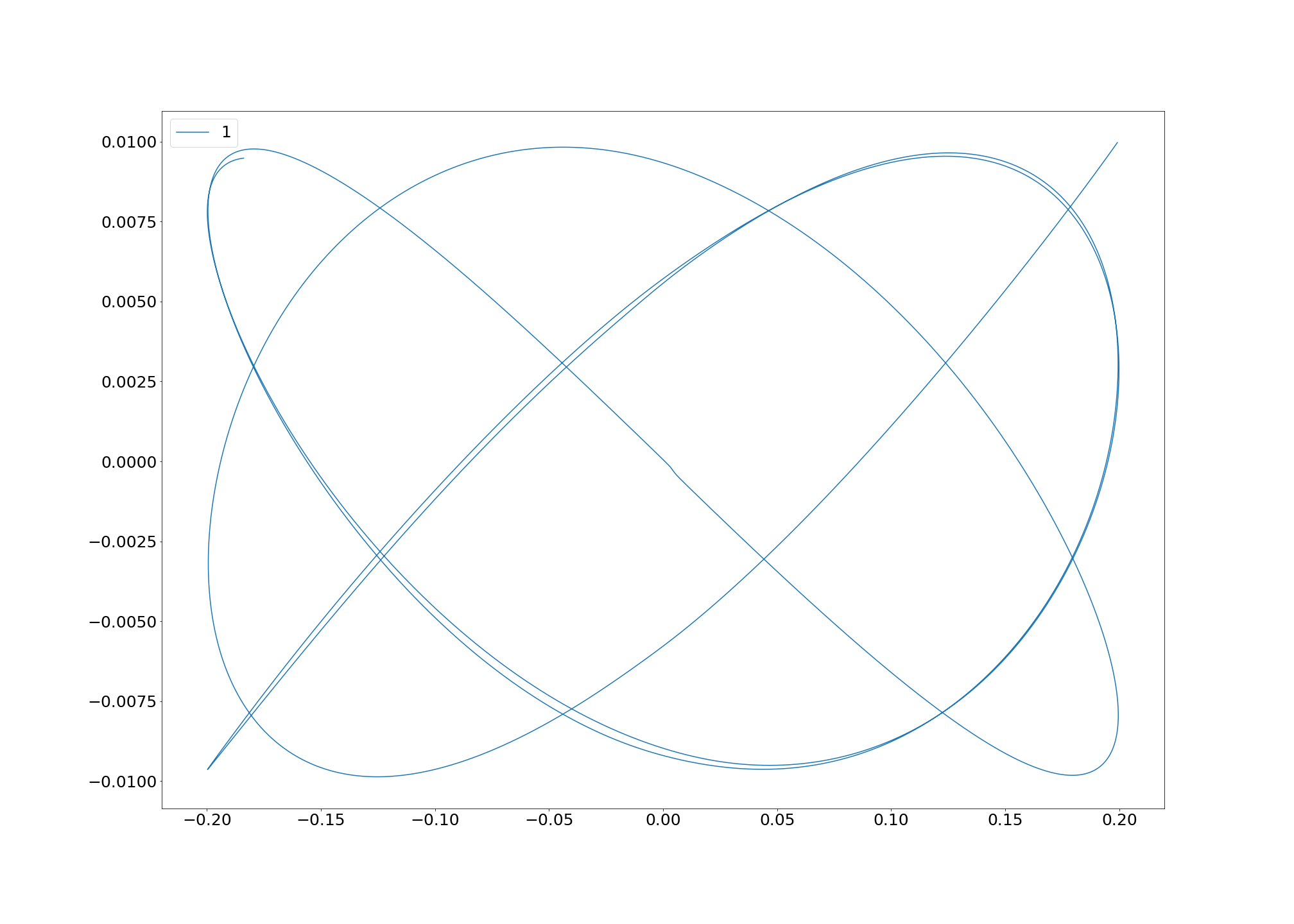
結構、実験と一致する曲線がかけて満足しています。
計算シミュレーションでなく、実験をする場合は洗濯に使う粉を使うとうまくいきます。
ただ、3次元になると、オイラー角でいう特異状態になり、計算値が爆発的に増加したり、nanで止まってうまくいかなかったり難しいです。
とりあえず、ムーアの一般逆行列ということにして処理していますが、どうすべきかは勉強が足りない為、わかりません。誰か教えて
今のところ、シミュレーションにはオイラー法を使用していますが、ルンゲルクッタ法を使ったほうがいい可能性があります。
ただ、数値爆発は計算精度の問題とは違う気もしてます。
2次元2重振り子
https://www.youtube.com/watch?v=25feOUNQB2Y
をシミュレーションした結果は(jifアニメなのでクリックして見てください)
とりあえず、それっぽくなっています。
オイラー・ラグランジュ方程式
ラグランジアン$L$
L=T-U\\
T:運動エネルギー\\
U:位置エネルギー
に対し、
\frac {\partial L}{\partial x} - \frac{d}{dt} \frac{\partial L}{\partial \dot{x}} = 0
が運動方程式となります。xは一般化位置であり、位置座標や回転角度などになります。
プラグラム
anaconda環境のpython2で実行しています。
1
オイラー・ラグランジュ方程式の大変さは、前述のとおり、
- 偏微分が多いため、計算ミスが起きやすい
- 偏微分後に同じ項をまとめるのがめんどい
- 多変数の一般座標になると、一般座標同士が絡み合い、$d^2 x_1 /dt^2=$ と $d^2 x_2 /dt^2 = $の形に分けるのが大変(シミュレーションをする分には分けなくても解ける)
実際に問題を解くと、たぶんうんざりします。
2
matlabやscilabを使える人は特に困らないでしょう。また、運動方程式導出後の微分方程式を解く際もode45等の解法が常備されているので、それでやればいいと思います。
ただ私は、$d^2 x_1 /dt^2=$ と $d^2 x_2 /dt^2 = $の形に直す方法が見つからず、力業で計算させることにしました。
3 コード
class Formula :
def __init__(self,L,num):
self.L = L
self.n = num #変数の種類数
def __add__(self,other):
self.L = np.append(self.L,other.L,axis =0)
self.together()
self.erase()
def __sub__(self,other):
self.L = np.append(self.L,-1*other.L,axis =0)
self.together()
self.erase()
def together(self): #同じ項の係数をまとめる
expr,vari = self.L.shape
if expr >=2:
for i in range(expr-1):
for j in range(i+1,expr):
m=0
while self.L[i][0+m*6:5+m*6].tolist() == self.L[j][0+m*6:5+m*6].tolist():
m += 1
if m == self.n:
break
if m== self.n:
self.L[i][5] += self.L[j][5]
for k in range(vari):
self.L[j][k] = 0
def erase(self): #係数が0の項を消す
expr,vari = self.L.shape
for i in list(reversed(range(expr))):
if self.L[i][5] == 0:
self.L = np.delete(self.L,i,axis = 0)
def partial(self,moji,kind): #kindの種類のもので項を偏微分する
expr,vari = self.L.shape
if kind == 0:
'''
sin
cos
+moji*6
'''
#print self.L
for i in range(expr):
if self.L[i][3+moji*6] !=0: #sin
hoge = copy.deepcopy(self.L[i])
hoge[5] = hoge[5]*hoge[3+moji*6]
hoge[3+moji*6] = hoge[3+moji*6]-1
hoge[4+moji*6] = hoge[4+moji*6]+1
self.L = np.append(self.L,hoge[np.newaxis,:],axis =0)
#print self.L
for i in range(expr):
if self.L[i][4+moji*6] !=0: #cos
hoge = copy.deepcopy(self.L[i])
hoge[5] = hoge[5]*hoge[4+moji*6]*-1
hoge[4+moji*6]= hoge[4+moji*6]-1
hoge[3+moji*6] = hoge[3+moji*6]+1
self.L = np.append(self.L,hoge[np.newaxis,:],axis =0)
#print self.L
'''
そのままのもの
次数を一つ下げる、0なら何もしない
元の次数を係数に掛ける
'''
#print self.L
for i in range(expr):
if self.L[i][kind] !=0:
#print kind,self.L[i][5]
self.L[i][5] = self.L[i][5] * self.L[i][kind+moji*6]
#print self.L[i][5]
self.L[i][kind+moji*6] = self.L[i][kind+moji*6] -1
else:
self.L[i][5] = 0 #含まないなら 0
if kind == 1:
'''
そのままのもの
次数を一つ下げる、0なら何もしない
元の次数を係数に掛ける
'''
for i in range(expr):
if self.L[i][kind+moji*6] !=0:
self.L[i][5] = self.L[i][5] * self.L[i][kind+moji*6]
self.L[i][kind+moji*6] = self.L[i][kind+moji*6] -1
else:
self.L[i][5] = 0 #含まないなら 0
self.together()
self.erase()
def diff(self): #時間微分
'''
4つのパターンで偏微分後
θ・の次数を1上げる
'''
L1=copy.deepcopy(self.L)
for i in range(self.n):
self.L =copy.deepcopy( L1)
self.partial(i,0)
expr,vari = self.L.shape
#print expr
#print self.L
for j in range(expr):
self.L[j][1+i*6] = self.L[j][1+i*6] + 1
if i == 0:
L2 = copy.deepcopy( self.L)
else:
L2 = np.append(L2,self.L,axis =0)
self.L =copy.deepcopy( L1)
self.partial(i,1)
expr,vari = self.L.shape
for j in range(expr):
self.L[j][2+i*6] += 1
L2 = np.append(L2,self.L,axis =0)
self.L = copy.deepcopy( L2)
self.together()
self.erase()
def disp(self): #多項式表示
print "-------------------Formula--------------"
expr,vari = self.L.shape
for j in range(expr):
hoge =""
for i in range(self.n):
hoge += str(self.L[j][5+i*6])
hoge += " θ^"
hoge += str(self.L[j][0+i*6])
hoge += " θ・^"
hoge += str(self.L[j][1+i*6])
hoge += " θ・・^"
hoge += str(self.L[j][2+i*6])
hoge += " sin^"
hoge += str(self.L[j][3+i*6])
hoge += " cos^"
hoge += str(self.L[j][4+i*6])
hoge += " "
hoge += " + "
print hoge
def subst(self,x): #代入 x ,x・の順に入れる
vari =np.array(x).shape
if vari[0] != self.n*2:
print "cannot subst"
else:
'''
行ベクトルを生成して
dotでLと をして、できたベクトルの全要素を足せばよい
'''
expr,vari = self.L.shape
sum1 = 0
hoge=0
for j in range(expr):
hoge=self.L[j][5] #係数
for i in range(self.n):
hoge = hoge*x[0+i*2]**self.L[j][0+i*6] #θ
hoge = hoge*x[1+i*2]**self.L[j][1+i*6] #θ・
hoge = hoge*math.sin(x[0+i*2])**self.L[j][3+i*6] #sin
hoge = hoge*math.cos(x[0+i*2])**self.L[j][4+i*6] #cos
sum1 += hoge
return sum1
self.L = 多項式の情報
self.n = 変数の数
self.L = [ [1, 2 ,3 , 4, 5, 6]
[7, 8, 9, 10,11,12]]
の場合
L = x^1*(\frac{d}{dt} x) ^2*(\frac{d^2}{dt^2} x) ^3 sin(x)^4 cos(x)^5 *6\\
+\\
x^7*(\frac{d}{dt} x) ^8*(\frac{d^2}{dt^2} x) ^9 sin(x)^{10} cos(x)^{11} *12\\
を表します。
関数は
L1+L2 : L1 = L1+L2 ちょっとわかりにくいですが
L1-L2 : L1 = L1-L2
*:実装していない
L1.partial(i,0) : $x_i$で偏微分
L1.partial(i,1) : $\frac{d}{dt} x_i$で偏微分
L1.diff() : 時間微分
L1.disp() : 多項式を表示
L1.disp2() : 表示をわかりやすくしたもの
を実装しています。
Y字振り子の運動方程式
次に、Y字振り子のシミュレーションをする方法について説明します。
Y字振り子は、V字角度は動きません。つまり、一方向の回転のみを許すピンジョインとといえます(Z-X平面のみを移動できる)。
天井にピンジョイントでつながった重りに、さらにボールジョイント(3つの回転を許す)で重りをつけるとY字振り子のモデルになります。
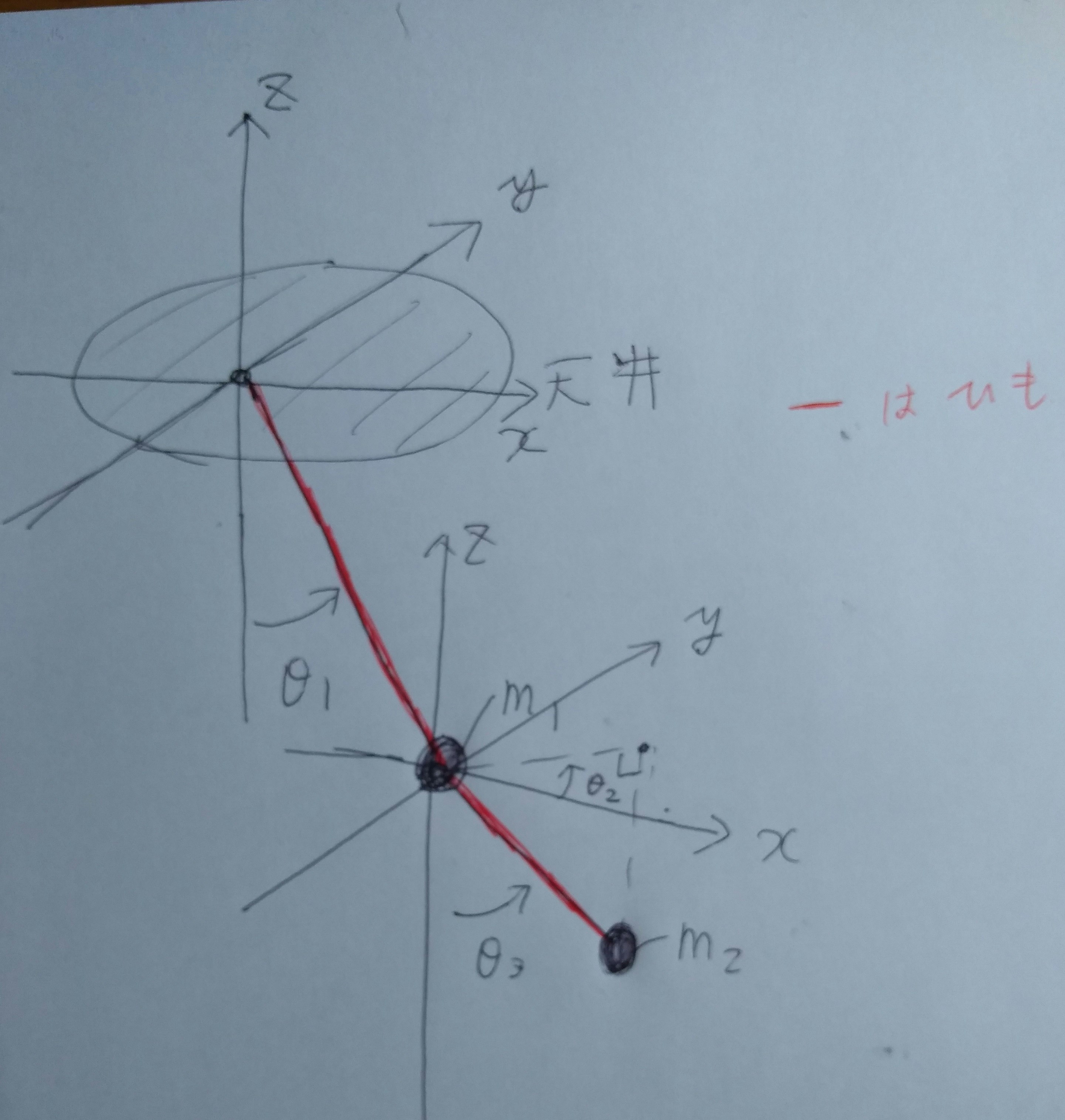
このように、回転角$\theta 123$を設定します。
\vec{R_{m1}} =
\left(
\begin{array}{ccc}
R_1*cos( \theta 1)\\
0\\
-R_1*sin(\theta2)
\end{array}
\right)
,
\vec{R_{m2}} = \vec{R_{m1}} +
\left(
\begin{array}{ccc}
R_3*sin(\theta3) * cos(\theta2)\\
R_3*sin(\theta3) * sin(\theta2)\\
-R_3*cos(\theta3)
\end{array}
\right)
となります。
これを時間微分し、速度ベクトルを出し、速度ベクトルの大きさから、運動エネルギーを出します。
T=\frac{1}{2} m_1 (R_1\dot{\theta})^2+\frac{1}{2} m_2 (R_1^2 \dot{\theta}^2 + R_3^2 sin(\theta 3)^2 \dot{\theta 2}^2 + R_3^2 \dot{\theta 3}^2
\\
-2*cos(\theta 1) sin(\theta 2) R_1 R_3 sin(\theta 3) \dot{\theta 1} \dot{\theta 2}\\
+2*(cos(\theta 1) cos(\theta 2) cos(\theta 3) + sin(\theta 1) sin(\theta 2) )R_1 R_3 \dot{\theta 1} \dot{\theta 3}
位置エネルギーは
U=m_1 g R_1 (1- cos(\theta 1)) + m_2 g (R_1 (1- cos(\theta 1)) + R_3(1-cos(\theta 3))
となる。
これを用いてラグランジアンを計算すると
L= m_1*r_1^2 /2 + m_2*r_1^2/2 \dot{ x_1}^{2.0} +
m_2 /2 *r_3^2 \dot{ x_2}^{2.0} sin( x_3)^{2.0} +
m_2 /2 *r_3^2 \dot{ x_3}^{2.0} +
m_2 /2 *(-2*r_1*r_3) \dot{ x_1}^{1.0} cos( x_1)^{1.0} \dot{ x_2}^{1.0} sin( x_2)^{1.0} sin( x_3)^{1.0} +
m_2 /2 *(2*r_1*r_3) \dot{ x_1}^{1.0} cos( x_1)^{1.0} cos( x_2)^{1.0} \dot{ x_3}^{1.0} cos( x_3)^{1.0} +
m_2 /2 *(2*r_1*r_3) \dot{ x_1}^{1.0} sin( x_1)^{1.0} \dot{ x_3}^{1.0} sin( x_3)^{1.0} +
-1*(g*(m_1*r1+m_2*(r_1+r_3))) +
-1*(-1*g*(m_1*r1+m_2*r_1)) cos( x_1)^{1.0} +
-1*(-1*g*m_2*r_3) cos( x_3)^{1.0}
となります。θとxを入れ替えて表示しています
x_1 = \theta 1
x_2 = \theta 2
x_3 = \theta 3
運動方程式を導くと
(m_2 /2 *(2*r_1*r_3) *1.0) + -1*( ( (m_2 /2 *(2*r_1*r_3) *1.0) *1.0) ) \dot{ x_1}^{1.0} cos( x_1)^{1.0} \dot{ x_3}^{1.0} sin( x_3)^{1.0} +
(m_2 /2 *(-2*r_1*r_3)*(-1)*1.0) + -1*( ( (m_2 /2 *(-2*r_1*r_3)*1.0) *(-1)*1.0) ) \dot{ x_1}^{1.0} sin( x_1)^{1.0} \dot{ x_2}^{1.0} sin( x_2)^{1.0} sin( x_3)^{1.0} +
(m_2 /2 *(2*r_1*r_3) *(-1)*1.0) + -1*( ( (m_2 /2 *(2*r_1*r_3) *1.0) *(-1)*1.0) ) \dot{ x_1}^{1.0} sin( x_1)^{1.0} cos( x_2)^{1.0} \dot{ x_3}^{1.0} cos( x_3)^{1.0} +
(-1*(-1*g*(m_1*r1+m_2*r_1))*(-1)*1.0) sin( x_1)^{1.0} +
0 + 0 + 0 +
0 + 0 +
0 +
-1*( ( (m_1*r_1^2 /2 + m_2*r_1^2/2*2.0) *1.0) ) \ddot { x_1}^{1.0} +
-1*( ( (m_2 /2 *(-2*r_1*r_3)*1.0) *1.0) ) cos( x_1)^{1.0} \dot{ x_2}^{2.0} cos( x_2)^{1.0} sin( x_3)^{1.0} +
-1*( ( (m_2 /2 *(2*r_1*r_3) *1.0) *(-1)*1.0) + ( (m_2 /2 *(-2*r_1*r_3)*1.0) *1.0) ) cos( x_1)^{1.0} \dot{ x_2}^{1.0} sin( x_2)^{1.0} \dot{ x_3}^{1.0} cos( x_3)^{1.0} +
-1*( ( (m_2 /2 *(-2*r_1*r_3)*1.0) *1.0) ) cos( x_1)^{1.0} \ddot { x_2}^{1.0} sin( x_2)^{1.0} sin( x_3)^{1.0} +
-1*( ( (m_2 /2 *(2*r_1*r_3) *1.0) *1.0) ) sin( x_1)^{1.0} \dot{ x_3}^{2.0} cos( x_3)^{1.0} +
-1*( ( (m_2 /2 *(2*r_1*r_3) *1.0) *(-1)*1.0) ) cos( x_1)^{1.0} cos( x_2)^{1.0} \dot{ x_3}^{2.0} sin( x_3)^{1.0} +
-1*( ( (m_2 /2 *(2*r_1*r_3) *1.0) *1.0) ) cos( x_1)^{1.0} cos( x_2)^{1.0} \ddot { x_3}^{1.0} cos( x_3)^{1.0} +
-1*( ( (m_2 /2 *(2*r_1*r_3) *1.0) *1.0) ) sin( x_1)^{1.0} \ddot { x_3}^{1.0} sin( x_3)^{1.0} =0\\
(m_2 /2 *(-2*r_1*r_3)*1.0) + -1*( ( (m_2 /2 *(-2*r_1*r_3)*1.0) *1.0) ) \dot{ x_1}^{1.0} cos( x_1)^{1.0} \dot{ x_2}^{1.0} cos( x_2)^{1.0} sin( x_3)^{1.0} +
(m_2 /2 *(2*r_1*r_3) *(-1)*1.0) + -1*( ( (m_2 /2 *(-2*r_1*r_3)*1.0) *1.0) ) \dot{ x_1}^{1.0} cos( x_1)^{1.0} sin( x_2)^{1.0} \dot{ x_3}^{1.0} cos( x_3)^{1.0} +
-1*( ( (m_2 /2 *(-2*r_1*r_3)*1.0) *(-1)*1.0) ) \dot{ x_1}^{2.0} sin( x_1)^{1.0} sin( x_2)^{1.0} sin( x_3)^{1.0} +
-1*( ( (m_2 /2 *(-2*r_1*r_3)*1.0) *1.0) ) \ddot { x_1}^{1.0} cos( x_1)^{1.0} sin( x_2)^{1.0} sin( x_3)^{1.0} +
0 + 0 +
-1*( ( (m_2 /2 *r_3^2*2.0) *1.0) ) \ddot { x_2}^{1.0} sin( x_3)^{2.0} +
-1*( ( (m_2 /2 *r_3^2*2.0) *2.0) ) \dot{ x_2}^{1.0} \dot{ x_3}^{1.0} sin( x_3)^{1.0} cos( x_3)^{1.0} =0\\
(m_2 /2 *r_3^2*2.0) \dot{ x_2}^{2.0} sin( x_3)^{1.0} cos( x_3)^{1.0} +
(m_2 /2 *(-2*r_1*r_3)*1.0) + -1*( ( (m_2 /2 *(2*r_1*r_3) *1.0) *(-1)*1.0) ) \dot{ x_1}^{1.0} cos( x_1)^{1.0} \dot{ x_2}^{1.0} sin( x_2)^{1.0} cos( x_3)^{1.0} +
(m_2 /2 *(2*r_1*r_3) *1.0) + -1*( ( (m_2 /2 *(2*r_1*r_3) *1.0) *1.0) ) \dot{ x_1}^{1.0} sin( x_1)^{1.0} \dot{ x_3}^{1.0} cos( x_3)^{1.0} +
(m_2 /2 *(2*r_1*r_3) *(-1)*1.0) + -1*( ( (m_2 /2 *(2*r_1*r_3) *1.0) *(-1)*1.0) ) \dot{ x_1}^{1.0} cos( x_1)^{1.0} cos( x_2)^{1.0} \dot{ x_3}^{1.0} sin( x_3)^{1.0} +
(-1*(-1*g*m_2*r_3)*(-1)*1.0) sin( x_3)^{1.0} +
-1*( ( (m_2 /2 *(2*r_1*r_3) *1.0) *1.0) ) \dot{ x_1}^{2.0} cos( x_1)^{1.0} sin( x_3)^{1.0} +
-1*( ( (m_2 /2 *(2*r_1*r_3) *1.0) *(-1)*1.0) ) \dot{ x_1}^{2.0} sin( x_1)^{1.0} cos( x_2)^{1.0} cos( x_3)^{1.0} +
-1*( ( (m_2 /2 *(2*r_1*r_3) *1.0) *1.0) ) \ddot { x_1}^{1.0} cos( x_1)^{1.0} cos( x_2)^{1.0} cos( x_3)^{1.0} +
-1*( ( (m_2 /2 *(2*r_1*r_3) *1.0) *1.0) ) \ddot { x_1}^{1.0} sin( x_1)^{1.0} sin( x_3)^{1.0} +
0 + 0 + 0 +
0 + 0 +
0 +
-1*( ( (m_2 /2 *r_3^2*2.0) *1.0) ) \ddot { x_3}^{1.0} =0
の3本の運動方程式が立ちます。
m1=1.0
m2=10
r1=1.0
r3=1.0
g=9.81
とすると
5.5 \dot{ x_1}^{2.0} +
5.0 \dot{ x_2}^{2.0} sin( x_3)^{2.0} +
5.0 \dot{ x_3}^{2.0} +
-10.0 \dot{ x_1}^{1.0} cos( x_1)^{1.0} \dot{ x_2}^{1.0} sin( x_2)^{1.0} sin( x_3)^{1.0} +
10.0 \dot{ x_1}^{1.0} cos( x_1)^{1.0} cos( x_2)^{1.0} \dot{ x_3}^{1.0} cos( x_3)^{1.0} +
10.0 \dot{ x_1}^{1.0} sin( x_1)^{1.0} \dot{ x_3}^{1.0} sin( x_3)^{1.0} +
206.01000000000002 +
-107.91000000000001 cos( x_1)^{1.0} +
-98.10000000000001 cos( x_3)^{1.0}
運動方程式を導くと
-107.91000000000001 sin( x_1)^{1.0} +
-11.0 \ddot { x_1}^{1.0} +
10.0 cos( x_1)^{1.0} \dot{ x_2}^{2.0} cos( x_2)^{1.0} sin( x_3)^{1.0} +
20.0 cos( x_1)^{1.0} \dot{ x_2}^{1.0} sin( x_2)^{1.0} \dot{ x_3}^{1.0} cos( x_3)^{1.0} +
10.0 cos( x_1)^{1.0} \ddot { x_2}^{1.0} sin( x_2)^{1.0} sin( x_3)^{1.0} +
-10.0 sin( x_1)^{1.0} \dot{ x_3}^{2.0} cos( x_3)^{1.0} +
10.0 cos( x_1)^{1.0} cos( x_2)^{1.0} \dot{ x_3}^{2.0} sin( x_3)^{1.0} +
-10.0 cos( x_1)^{1.0} cos( x_2)^{1.0} \ddot { x_3}^{1.0} cos( x_3)^{1.0} +
-10.0 sin( x_1)^{1.0} \ddot { x_3}^{1.0} sin( x_3)^{1.0} =0\\
-10.0 \dot{ x_1}^{2.0} sin( x_1)^{1.0} sin( x_2)^{1.0} sin( x_3)^{1.0} +
10.0 \ddot { x_1}^{1.0} cos( x_1)^{1.0} sin( x_2)^{1.0} sin( x_3)^{1.0} +
-10.0 \ddot { x_2}^{1.0} sin( x_3)^{2.0} +
-20.0 \dot{ x_2}^{1.0} \dot{ x_3}^{1.0} sin( x_3)^{1.0} cos( x_3)^{1.0} =0\\
10.0 \dot{ x_2}^{2.0} sin( x_3)^{1.0} cos( x_3)^{1.0} +
-98.10000000000001 sin( x_3)^{1.0} +
-10.0 \dot{ x_1}^{2.0} cos( x_1)^{1.0} sin( x_3)^{1.0} +
10.0 \dot{ x_1}^{2.0} sin( x_1)^{1.0} cos( x_2)^{1.0} cos( x_3)^{1.0} +
-10.0 \ddot { x_1}^{1.0} cos( x_1)^{1.0} cos( x_2)^{1.0} cos( x_3)^{1.0} +
-10.0 \ddot { x_1}^{1.0} sin( x_1)^{1.0} sin( x_3)^{1.0} +
-10.0 \ddot { x_3}^{1.0} = 0
の3本の運動方程式が立ちます。
この方程式を用いてシミュレーションさせます。
シミュレーションコード(オイラー法)
速度から位置を $r_{n+1}= r_{n} +v{n} *DT$
加速度から速度を $v_{n+1}= v_{n} +a{n} *DT$
更新することで、シミュレーションします。
# -*- coding: utf-8 -*-
"""
Created on Sat Mar 21 14:11:03 2020
@author: kisim
"""
import numpy as np # Numpyライブラリ
import copy
import math
# import matplotlib.pyplot as plt
import matplotlib
# matplotlib.use('Agg') # -----(1)
import matplotlib.pyplot as plt
import matplotlib.animation as animation
from matplotlib.animation import PillowWriter
'''
数式処理プログラム
列 : 多項式
行 : θ θ・ θ・・ sinθ cosθ 係数
の6個 × 変数数
'''
class Formula :
def __init__(self,L,num):
self.L = L
self.n = num #変数の種類数
def __add__(self,other):
self.L = np.append(self.L,other.L,axis =0)
self.together()
self.erase()
def __sub__(self,other):
expr,vari = other.L.shape
hoge = copy.deepcopy(other.L)
for i in range(expr):
hoge[i][5] = hoge[i][5] * -1
self.L = np.append(self.L,hoge,axis =0)
self.together()
self.erase()
def together(self): #同じ項の係数をまとめる
expr,vari = self.L.shape
if expr >=2:
for i in range(expr-1):
for j in range(i+1,expr):
m=0
while self.L[i][0+m*6:5+m*6].tolist() == self.L[j][0+m*6:5+m*6].tolist():
m += 1
if m == self.n:
break
if m== self.n:
self.L[i][5] += self.L[j][5]
for k in range(vari):
self.L[j][k] = 0
def erase(self): #係数が0の項を消す
expr,vari = self.L.shape
for i in list(reversed(range(expr))):
if self.L[i][5] == 0:
self.L = np.delete(self.L,i,axis = 0)
def partial(self,moji,kind): #kindの種類のもので項を偏微分する
expr,vari = self.L.shape
if kind == 0:
'''
sin
cos
+moji*6
'''
#print self.L
for i in range(expr):
if self.L[i][3+moji*6] !=0: #sin
hoge = copy.deepcopy(self.L[i])
hoge[5] = hoge[5]*hoge[3+moji*6]
hoge[3+moji*6] = hoge[3+moji*6]-1
hoge[4+moji*6] = hoge[4+moji*6]+1
self.L = np.append(self.L,hoge[np.newaxis,:],axis =0)
#print self.L
for i in range(expr):
if self.L[i][4+moji*6] !=0: #cos
hoge = copy.deepcopy(self.L[i])
hoge[5] = hoge[5]*hoge[4+moji*6]*-1
hoge[4+moji*6]= hoge[4+moji*6]-1
hoge[3+moji*6] = hoge[3+moji*6]+1
self.L = np.append(self.L,hoge[np.newaxis,:],axis =0)
#print self.L
'''
そのままのもの
次数を一つ下げる、0なら何もしない
元の次数を係数に掛ける
'''
#print self.L
for i in range(expr):
if self.L[i][kind] !=0:
#print kind,self.L[i][5]
self.L[i][5] = self.L[i][5] * self.L[i][kind+moji*6]
#print self.L[i][5]
self.L[i][kind+moji*6] = self.L[i][kind+moji*6] -1
else:
self.L[i][5] = 0 #含まないなら 0
if kind == 1:
'''
そのままのもの
次数を一つ下げる、0なら何もしない
元の次数を係数に掛ける
'''
for i in range(expr):
if self.L[i][kind+moji*6] !=0:
self.L[i][5] = self.L[i][5] * self.L[i][kind+moji*6]
self.L[i][kind+moji*6] = self.L[i][kind+moji*6] -1
else:
self.L[i][5] = 0 #含まないなら 0
self.together()
self.erase()
def diff(self): #時間微分
'''
4つのパターンで偏微分後
θ・の次数を1上げる
'''
L1=copy.deepcopy(self.L)
for i in range(self.n):
self.L =copy.deepcopy( L1)
self.partial(i,0)
expr,vari = self.L.shape
#print expr
#print self.L
for j in range(expr):
self.L[j][1+i*6] = self.L[j][1+i*6] + 1
if i == 0:
L2 = copy.deepcopy( self.L)
else:
L2 = np.append(L2,self.L,axis =0)
self.L =copy.deepcopy( L1)
self.partial(i,1)
expr,vari = self.L.shape
for j in range(expr):
self.L[j][2+i*6] += 1
L2 = np.append(L2,self.L,axis =0)
self.L = copy.deepcopy( L2)
self.together()
self.erase()
def disp(self): #多項式表示
print "-------------------Formula--------------"
expr,vari = self.L.shape
for j in range(expr):
hoge =""
for i in range(self.n):
hoge += str(self.L[j][5+i*6])
hoge += " θ^"
hoge += str(self.L[j][0+i*6])
hoge += " θ・^"
hoge += str(self.L[j][1+i*6])
hoge += " θ・・^"
hoge += str(self.L[j][2+i*6])
hoge += " sin^"
hoge += str(self.L[j][3+i*6])
hoge += " cos^"
hoge += str(self.L[j][4+i*6])
hoge += " "
hoge += " + "
print hoge
def disp2(self): #多項式表示
print "-------------------Formula--------------"
expr,vari = self.L.shape
for j in range(expr):
hoge =""
for i in range(self.n):
hoge += "["+str(i+1)+" "
if self.L[j][5]!= 0:
if i == 0:
hoge += str(self.L[j][5+i*6])
if self.L[j][0+i*6]!= 0:
hoge += " θ^"
hoge += str(self.L[j][0+i*6])
if self.L[j][1+i*6]!= 0:
hoge += " θ・^"
hoge += str(self.L[j][1+i*6])
if self.L[j][2+i*6]!= 0:
hoge += " θ・・^"
hoge += str(self.L[j][2+i*6])
if self.L[j][3+i*6]!= 0:
hoge += " sin^"
hoge += str(self.L[j][3+i*6])
if self.L[j][4+i*6]!= 0:
hoge += " cos^"
hoge += str(self.L[j][4+i*6])
hoge += " ] "
hoge += " + "
print hoge
def latex(self):
variable = " x"
k=1
print "-------------------Formula--------------"
expr,vari = self.L.shape
for j in range(expr):
hoge =""
for i in range(self.n):
hoge += " "
if self.L[j][5]!= 0:
if i == 0:
hoge += str(self.L[j][5+i*6])
if self.L[j][0+i*6]!= 0:
hoge += variable+"_"+str(i+k)+"^{"
hoge += str(self.L[j][0+i*6])+"}"
if self.L[j][1+i*6]!= 0:
hoge += " \dot{"+variable+"_"+str(i+k)+"}^{"
hoge += str(self.L[j][1+i*6])+"}"
if self.L[j][2+i*6]!= 0:
hoge += " \ddot {"+variable+"_"+str(i+k)+"}^{"
hoge += str(self.L[j][2+i*6])+"}"
if self.L[j][3+i*6]!= 0:
hoge += " sin("+variable+"_"+str(i+k)+")^{"
hoge += str(self.L[j][3+i*6])+"}"
if self.L[j][4+i*6]!= 0:
hoge += " cos("+variable+"_"+str(i+k)+")^{"
hoge += str(self.L[j][4+i*6])+"}"
hoge += " "
hoge += " + "
print hoge
def subst(self,x): #代入 x ,x・の順に入れる
vari =np.array(x).shape
if vari[0] != self.n*2:
print "cannot subst"
else:
'''
行ベクトルを生成して
dotでLと をして、できたベクトルの全要素を足せばよい
'''
expr,vari = self.L.shape
sum1 = 0
hoge=0
for j in range(expr):
hoge=self.L[j][5] #係数
for i in range(self.n):
hoge = hoge*x[0+i*2]**self.L[j][0+i*6] #θ
hoge = hoge*x[1+i*2]**self.L[j][1+i*6] #θ・
hoge = hoge*math.sin(x[0+i*2])**self.L[j][3+i*6] #sin
hoge = hoge*math.cos(x[0+i*2])**self.L[j][4+i*6] #cos
sum1 += hoge
return sum1
def separete(self): #2変数と考えて、 1 2 b の3つに分割する
a1=np.asarray([[]])
a2=np.asarray([[]])
expr,vari = self.L.shape
for j in range(expr)[::-1]:
if self.L[j][2] == 1:
if len(a1[0]) == 0:
a1=(self.L[j]) [np.newaxis,:]
else:
a1 = np.append(a1,(self.L[j]) [np.newaxis,:],axis =0)
self.L = np.delete(self.L,j,0)
continue
if self.L[j][8] == 1:
if len(a2[0]) == 0:
a2=(self.L[j]) [np.newaxis,:]
else:
a2 = np.append(a1,(self.L[j]) [np.newaxis,:],axis =0)
self.L = np.delete(self.L,j,0)
continue
if len(a1[0]) == 0:
a1 =np.asarray([ [0,0,0,0,0,0 ,0,0,0,0,0,0]])
if len(a2[0]) == 0:
a2 = np.asarray([[0,0,0,0,0,0 ,0,0,0,0,0,0]])
L1 = Formula(a1,2)
L2 = Formula(a2,2)
return L1,L2
def separete3(self): #3変数と考えて、 1 2 3 b の 4 つに分割する
a1=np.asarray([[]])
a2=np.asarray([[]])
a3=np.asarray([[]])
expr,vari = self.L.shape
for j in range(expr)[::-1]:
print "a1"
print a1.shape
print "a3"
print a3.shape
print "a2"
print a2.shape
if self.L[j][2] == 1:
if len(a1[0]) == 0:
a1=(self.L[j]) [np.newaxis,:]
else:
a1 = np.append(a1,(self.L[j]) [np.newaxis,:],axis =0)
self.L = np.delete(self.L,j,0)
continue
if self.L[j][8] == 1:
if len(a2[0]) == 0:
a2=(self.L[j]) [np.newaxis,:]
else:
a2 = np.append(a2,(self.L[j]) [np.newaxis,:],axis =0)
self.L = np.delete(self.L,j,0)
continue
if self.L[j][14] == 1:
if len(a3[0]) == 0:
a3=(self.L[j]) [np.newaxis,:]
else:
a3 = np.append(a3,(self.L[j]) [np.newaxis,:],axis =0)
self.L = np.delete(self.L,j,0)
continue
if len(a1[0]) == 0:
a1 =np.asarray([ [0,0,0,0,0,0 ,0,0,0,0,0,0 ,0,0,0,0,0,0]])
if len(a2[0]) == 0:
a2 = np.asarray([[0,0,0,0,0,0 ,0,0,0,0,0,0 ,0,0,0,0,0,0]])
if len(a3[0]) == 0:
a3 = np.asarray([[0,0,0,0,0,0 ,0,0,0,0,0,0 ,0,0,0,0,0,0]])
L1 = Formula(a1,3)
L2 = Formula(a2,3)
L3 = Formula(a3,3)
return L1,L2,L3
# L= np.asarray([[7,2,3,4,5,6, 7,2,3,4,5,6]])
# L= np.asarray([[2,2,0,5,4,5],[2,2,0,5,4,5]])
'''
L1,L2 の二つしか 式がなく、変数も2つの場合で考えよう
式 ≒ 0 として、
θ・・の項のみ取り出し新しいインスタンス化
除かれた方をbとして[L1_b,L2_b]ベクトルを作る
θ・・の項は
[L1_1 L1_2
L2_1 L2_2 ] というインスタンスの行列 A を考える
L1_2 = L1の式の中の θ2・・の項
θ・・ = A^-1 b を計算
オイラー法の陽解法でθ・ θ も出てくる
ここまでやってみよう
L1_b,L1_1,L1_2 を生成する 方法を考える
'''
m1=1.0
m2=10
r1=1.0
r3=1.0
g=9.81
T1=np.array([[0,2,0,0,0,m1*r1**2 /2 + m2*r1**2/2,
0,0,0,0,0,1,
0,0,0,0,0,1]])
T2=np.array([[0,0,0,0,0,m2 /2 *r3**2 ,
0,2,0,0,0,1,
0,0,0,2,0,1]])
T3=np.array([[0,0,0,0,0,m2 /2 *r3**2 ,
0,0,0,0,0,1,
0,2,0,0,0,1]])
T4=np.array([[0,1,0,0,1,m2 /2 *(-2*r1*r3),
0,1,0,1,0,1,
0,0,0,1,0,1]])
T5=np.array([[0,1,0,0,1,m2 /2 *(2*r1*r3) ,
0,0,0,0,1,1,
0,1,0,0,1,1]])
T6=np.array([[0,1,0,1,0,m2 /2 *(2*r1*r3) ,
0,0,0,0,0,1,
0,1,0,1,0,1]])
print "T1"
T=Formula(T1,3)
T.disp2()
print "T2"
R=Formula(T2,3)
R.disp2()
T+R
print "T3"
R=Formula(T3,3)
R.disp2()
T+R
print "T4"
R=Formula(T4,3)
R.disp2()
T+R
print "T5"
R=Formula(T5,3)
R.disp2()
T+R
print "T6"
R=Formula(T6,3)
R.disp2()
T+R
print "T"
T.disp2()
U1=np.array([[0,0,0,0,0,g*(m1*r1+m2*(r1+r3)),
0,0,0,0,0,1,
0,0,0,0,0,1]])
U2=np.array([[0,0,0,0,1,-1*g*(m1*r1+m2*r1),
0,0,0,0,0,1,
0,0,0,0,0,1]])
U3=np.array([[0,0,0,0,0,-1*g*m2*r3,
0,0,0,0,0,1,
0,0,0,0,1,1]])
U = Formula(U1,3)
hoge = Formula(U2,3)
U+hoge
hoge = Formula(U3,3)
U+hoge
print "U"
U.disp2()
T1=copy.deepcopy(T)
T1+U
T-U
L=copy.deepcopy(T)
# ラグランジュ方程式の構築
Lt_1=copy.deepcopy(T)
Lt_2=copy.deepcopy(T)
Lt_1.partial(0,0)
Lt_2.partial(0,1)
Lt_2.diff()
Lt_1-Lt_2
Ls_1=copy.deepcopy(T)
Ls_2=copy.deepcopy(T)
Ls_1.partial(1,0)
Ls_2.partial(1,1)
Ls_1.disp2()
print "Ls_2"
Ls_2.disp2()
Ls_2.diff()
Ls_2.disp2()
Ls_1-Ls_2
Lr_1=copy.deepcopy(T)
Lr_2=copy.deepcopy(T)
Lr_1.partial(2,0)
Lr_2.partial(2,1)
Lr_2.diff()
Lr_1-Lr_2
L1t=copy.deepcopy(Lt_1)
L1t_1,L1t_2,L1t_3 = L1t.separete3()
L2t=copy.deepcopy(Ls_1)
L2t_1,L2t_2,L2t_3 = L2t.separete3()
L3t=copy.deepcopy(Lr_1)
L3t_1,L3t_2,L3t_3 = L3t.separete3()
'''
オイラー法による数値解法を行う
初期値設定
解法
表示
の3プロセスを実装する必要がある
'''
DT = 0.0001 #時刻
x=np.array([0.1,0,0.1,0,0.1,0]) #初期値
saveX = x
T=10
N=int(T/DT) #計算時間/DT
saveEnergy = np.asarray([T1.subst(x)])
for i in range(N):
b1 = L1t.subst(x) * -1
b2 = L2t.subst(x) * -1
b3 = L3t.subst(x) * -1
a11 = L1t_1.subst(x)
a12 = L1t_2.subst(x)
a13 = L1t_3.subst(x)
a21 = L2t_1.subst(x)
a22 = L2t_2.subst(x)
a23 = L2t_3.subst(x)
a31 = L3t_1.subst(x)
a32 = L3t_2.subst(x)
a33 = L3t_3.subst(x)
B=np.array([b1,b2,b3])
B=B.reshape([3,1])
A=np.array([a11,a12,a13,a21,a22,a23,a31,a32,a33])
A=A.reshape([3,3])
hoge = np.linalg.det(A)
if hoge == 0:
#N=i
#print "hoge = 0 break"
Aneg = np.linalg.pinv(A)
else:
Aneg = np.linalg.inv(A)
'''
if hoge < 0.001:
N=i
print "hoge > 10000 break"
break
'''
K = np.dot(Aneg,B)
x2 =np.array( x ) + np.array( [ x[1] ,K[0][0] ,x[3], K[1][0], x[5] ,K[2][0] ] ) * DT
x = x2
saveX = np.append(saveX,x, axis=0)
Energy = T1.subst(x)
saveEnergy = np.append(saveEnergy,[Energy], axis=0)
saveX = saveX.reshape([6,N+1],order ='F')
t=[float(i)*DT for i in range(N+1)]
t= np.asarray(t)
# 点履歴
position_x1=r1*np.sin(saveX[0]) +r3*np.sin(saveX[4])*np.cos(saveX[2])
position_y1=r3*np.sin(saveX[4])*np.sin(saveX[2])
plt.figure(figsize=(28, 20)) # (width, height)
plt.rcParams["font.size"] = 25
plt.plot(position_x1,position_y1,label ="1")
plt.legend(fontsize = 25)
plt.savefig('Position_test.png')
# グラフ化
# z=np.sin(saveX[0])*R1+np.sin(saveX[2])*r2
plt.figure(figsize=(28, 20)) # (width, height)
plt.rcParams["font.size"] = 25
plt.xlim(0,T)
# plt.plot(t,z,label ="z")
plt.plot(t,saveX[0],label="x0")
plt.plot(t,saveX[1],label="dt x0")
plt.plot(t,saveX[2],label="x1")
plt.plot(t,saveX[3],label="dt x1")
plt.plot(t,saveX[4],label="x2")
plt.plot(t,saveX[5],label="dt x2")
plt.legend(fontsize = 25)
plt.savefig('Pendulum_test.png')
plt.figure(figsize=(28, 20)) # (width, height)
plt.rcParams["font.size"] = 25
plt.xlim(0,T)
# plt.plot(t,z,label ="z")
plt.plot(t,saveEnergy,label="Energy")
plt.legend(fontsize = 25)
plt.savefig('Energy_test.png')
こんな感じで、リサージュ曲線がかけます。