線形重回帰による決定係数の算出とモデルの選択 part_2

はじめに

　線形回帰を実施するとき、どのモデルが最も効率が良いのか試行する。データはscikit-learnのbreast_cancerを用いて実装する。このデータはウィスコンシン乳癌データセットと呼ばれるもので、腫瘍が良性であるか悪性であるかを判定したものである。データは569あり、そのうち良性は212、悪性は357、特徴量は30種類ある。これらのデータを用いて腫瘍が良性か悪性かを判定するモデルを作成し、最も決定係数が高くなるものを選択する。

　前回、線形重回帰による決定係数の算出とモデルの選択にて線形回帰、Lasso回帰、Ridge回帰、ElasticNet回帰の決定係数を求めた。ElasticNet回帰のli_ratioは0.5のみ実施したため、決定係数が最大となるli_ratioと決定係数を求める。

#シリーズ

• 線形重回帰による決定係数の算出とモデルの選択
• 線形重回帰による決定係数の算出とモデルの選択 part_2
• 単回帰分析による寄与率の算出
• 線形回帰と特徴量の絞り込み
• ロジスティック回帰(分類)とハイパーパラメータのチューニング
• 線形SVC(分類)とハイパーパラメータのチューニング
• 非線形SVC(分類)とハイパーパラメータのチューニング
• 決定木とハイパーパラメータのチューニング
• 決定木とハイパーパラメータのチューニング２

前回の結果

線形回帰の手法	メソッド	汎化手法	決定係数
線形回帰	LinearRegression()	-	0.73
Lasso回帰	Lasso()	L1正則化	0.61
Ridge回帰	Ridge()	L2正則化	0.72
ElasticNet回帰	ElasticNet()	L1 & L2正則化	0.66
※ElasticNet回帰はL1：L2 = 50：50

今回の結果

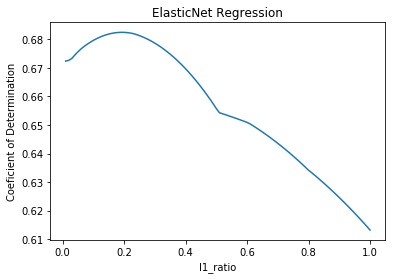
L1：L2 = 19：81のとき決定係数は最大で0.68となる。（l1_ratio=0.19）

手順

• 乳癌のデータセットを読み込む
• 訓練データとテストデータを分離する
• 決定係数の最大値を初期化し、li_ratioと決定係数を入れるための空のリストを用意する
• li_ratioと決定係数をプロットする
• 決定係数最大となるときのli_ratioと決定係数を出力する

#pythonによる実装

import numpy as np
from sklearn.datasets import load_breast_cancer
from sklearn.linear_model import ElasticNet
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt

#データの読み込み
cancer_data = load_breast_cancer()

#データポイントと特徴量(569,30)
print("データポイントと特徴量\n{}".format(cancer_data.data.shape))
print("")

#訓練データとテストデータを分離
train_X, test_X, train_y, test_y = train_test_split(cancer_data.data, cancer_data.target, random_state=0)

#モデルを学習し、最も高いl1の値と決定係数を出力する
maxvalue = 0
x = []
y = []

for i in range(1, 101):
    j = i / 100
    model = ElasticNet(l1_ratio=j)
    model.fit(train_X, train_y)
    score = model.score(test_X, test_y)

    x.append(j)
    y.append(score)

    if score >= maxvalue:
        maxvalue = score
        k = j

plt.xlabel("l1_ratio")
plt.ylabel("Coeficient of Determination")
plt.plot(x, y)
plt.show()

print("最も決定係数が高くなるli_ratioは：{}".format(k))
print("最も高い決定係数は：{:.2f}".format(maxvalue))

出力

データポイントと特徴量
(569, 30)

最も決定係数が高くなるli_ratio：0.19
最も高い決定係数は：0.68

おわりに

　ElasticNet回帰で決定係数が最大となるli_ratioを求めることができた。しかし、線形回帰には及ばなかったためモデルは線形回帰を選定する。