はじめに

　線形回帰を実施するとき、どのモデルが最も効率が良いのか試行する。データはscikit-learnのbreast_cancerを用いて実装する。このデータはウィスコンシン乳癌データセットと呼ばれるもので、腫瘍が良性であるか悪性であるかを判定したものである。データは569あり、そのうち良性は212、悪性は357、特徴量は30種類ある。これらのデータを用いて腫瘍が良性か悪性かを判定するモデルを作成し、最も決定係数が高くなるものを選択する。

　これまでの経緯から最も決定係数の大きくなるモデルは線形回帰だったが、決定係数は0.73と高くなかった。決定係数を高めるため、寄与率の高い特徴量を抽出して決定係数を求める。

シリーズ

結果

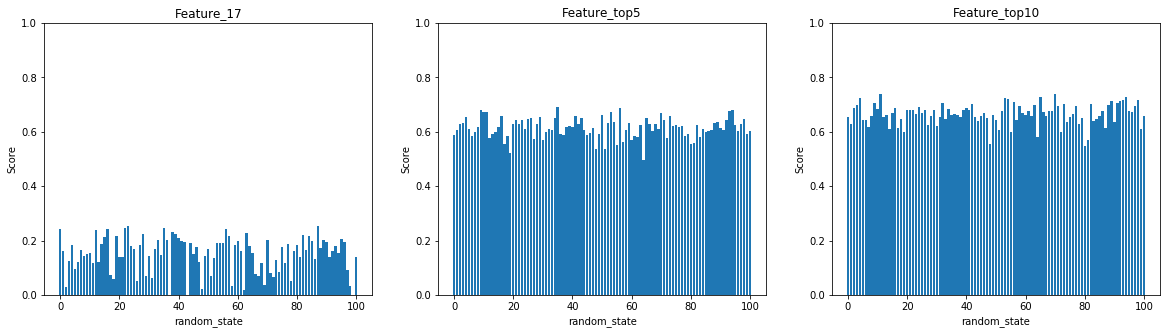
　x軸はrandam_stateを0～100まで振った。y軸はScoreを表す。
　左の図が最も高い寄与率の特徴量のみを用いた単回帰分析。これだけを用いては高い決定係数は得られないことがわかった。真ん中の図が寄与率Top5、右の図が寄与率Top10を用いた重回帰分析。単回帰分析に比べて決定係数は上昇したが、それでも値は低い。

手順

乳癌データの読み込み
データの前処理
17番目の特徴量のみで単回帰分析
寄与率上位5種で回帰分析
寄与率上位10種で回帰分析
データのプロット

pythonによる実装

import numpy as np
import pandas as pd
from sklearn.datasets import load_breast_cancer
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt

#データの読み込み
cancer_data = load_breast_cancer()
j = []
value_1 = []
value_2 = []
value_3 = []

#データの前処理
df =pd.DataFrame(cancer_data.data)
df_1 = df.drop(range(0, 4), axis=1)
df_1 = df_1.drop(range(5, 7), axis=1)
df_1 = df_1.drop(range(9, 14), axis=1)
df_1 = df_1.drop(16, axis=1)
df_1 = df_1.drop(18, axis=1)
df_1 = df_1.drop(range(20, 24), axis=1)
df_1 = df_1.drop(range(25, 27), axis=1)
df_1 = df_1.drop(28, axis=1)

df_2 = df_1.drop(8, axis=1)
df_2 = df_2.drop(15, axis=1)
df_2 = df_2.drop(24, axis=1)
df_2 = df_2.drop(27, axis=1)
df_2 = df_2.drop(29, axis=1)

#17番目の特徴量のみで単回帰分析
for i in range(0, 101):
    train_X, test_X, train_y, test_y = train_test_split(cancer_data.data[:, 17], cancer_data.target, random_state=i)

    train_X = train_X.reshape((-1, 1))
    test_X = test_X.reshape((-1, 1))

    model = LinearRegression()
    model.fit(train_X, train_y)

    j.append(i)
    value_1.append(model.score(test_X, test_y))

#寄与率上位5種で回帰分析
for i in range(0, 101):
    train_X, test_X, train_y, test_y = train_test_split(df_2, cancer_data.target, random_state=i)

    model = LinearRegression()
    model.fit(train_X, train_y)

    value_2.append(model.score(test_X, test_y))

#寄与率上位10種で回帰分析
for i in range(0, 101):
    train_X, test_X, train_y, test_y = train_test_split(df_1, cancer_data.target, random_state=i)

    model = LinearRegression()
    model.fit(train_X, train_y)

    value_3.append(model.score(test_X, test_y))

#データのプロット
fig = plt.figure(figsize=(20, 5))
plt.subplots_adjust(wspace=0.2)
ax = fig.add_subplot(1, 3, 1)
ax.plot(j, value_1)
ax.set_title("Feature_17")
ax.set_xlabel("random_state")
ax.set_ylabel("Score")
ax.set_ylim([0, 1])

ax = fig.add_subplot(1, 3, 2)
ax.plot(j, value_2)
ax.set_title("Feature_top5")
ax.set_xlabel("random_state")
ax.set_ylabel("Score")
ax.set_ylim([0, 1])

ax = fig.add_subplot(1, 3, 3)
ax.plot(j, value_3)
ax.set_title("Feature_17")
ax.set_xlabel("random_state")
ax.set_ylabel("Score")
ax.set_ylim([0, 1])

plt.show()

おわりに

　線形回帰では限界を感じた。しかし、寄与率の算出には有用と思われる。高い決定係数を求めるにはその他のモデルで試行していく。

線形回帰と特徴量の絞り込み

はじめに

結果

手順

pythonによる実装

おわりに