予測と結果の合致性の評価
はじめに
- 今回は、説明可能性についての5回目となります。今回は、モデルを評価するための指標の1つであるLog lossについてまとめています。
- Log lossはMLのモデルを評価する指標の1つであり、モデルをチューニングしていく際の指標としても利用されています。
- 説明可能性についてのまとめはこちらになります。
Log lossとは
- ログ損失、Logarithmic Loss、Log lossなどと言われていますが、予測された確率とその結果の乖離を交差エントロピーを利用して数値化しているものです。
- こちらでも書いた通りに(Predictが、「勝つ」か「負ける」を予測することであり、Forecastはどれくらいの確率で勝つのか(または負けるのか)を予測すること。)、Forecastにこだわりたい私としては、予測した確率の精度は重要な指標の1つとなります。
- モデルがいいほど0に近くなり、完璧なモデルでLog損失が0になります。
- すでに各種ライブラリに組み込まれているほど一般的な指標ですが、実際に何を見ているのかを整理するために、ここでも文章として説明します。
Accuracy、Brier Scoreとの違い
- Accuracyは0か1を予測し、その結果を評価しています。確率の高い・低いは、0か1を予測するために利用されていますが、予測した確率の乖離については考慮されていません。
- Brier Scoreについては以前に書きましたが(機械学習のモデル評価と説明可能性のための指標 その3。Brier Score(ブライアスコア))こちらの評価に近い考え方です。
どちらも予測した確率と結果の乖離を数値化していますが、その計算方法が違うだけです。
数学的計算方法
- 2項分類の計算式は下記の通りとなります。多項分類についてはここでは省略します。
log : 対数関数(底は$e$)
$y$ : Lable。0か1の2項分類。
$p$ : 予測確率。通常prediction_proba。
$$
-(y {\log} p+(1-y){\log}(1-p))
$$
- 平均値となるので
$$-\frac{1}{N} \sum_{i=1}^N((y_i {\log} p_i+(1-y_i){\log}(1-p_i))$$
- ちなみにさきほどのBrier Scoreは
$$\frac{1}{N} \sum_{i=1}^N(F_i - A_i)^2$$
Pythonでの計算
- Pythonで実際に計算してみると、より中身が把握できると思います。
個別のLog lossの計算
-
コードはこちら
# log loss import numpy as np import math def logloss(true_label, predicted, eps=1e-15): p = np.clip(predicted, eps, 1 - eps) if true_label == 1: return -math.log(p) else: return -math.log(1 - p) -
Labelが1で1の確率が0.9の時
logloss(1,0.9)out> 0.10536051565782628
-
Labelが0で1の確率が0.2の時
logloss(0,0.2)out> 0.2231435513142097
-
色々なLabelと確率を変動させるとLog lossの値がどう変化するかがよりイメージできると思います。たとえば、Labelが0だが、1になる確率を0.9と予測した場合、下記のようにLog lossの値が大きくなり評価が悪化します。
logloss(0,0.9)out> 2.302585092994046
-
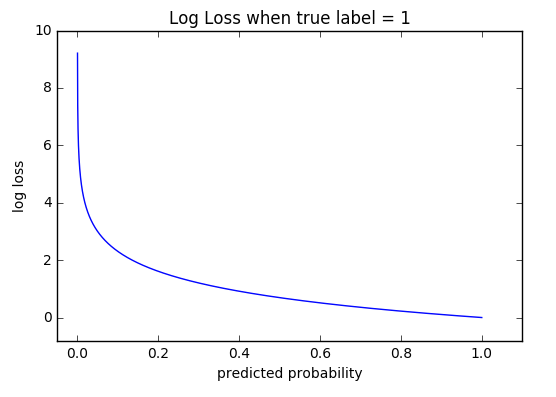
上記のようにlabel1の時の確率を変動させていくと、下図のようなプロットになります。Label=1で1になる確率が1に近づくほどLog lossが0に近づき、1になる確率が0に近い(間違っていた)ところで極端に数値が上昇しています。
-
コードから見てわかる通り、対数関数にLabelが0の時は、0になる確率を、Labelが1の時には1になる確率を代入して求めています。
-math.log(0.9)out> 0.10536051565782628
モデル全体のLog lossの計算
-
モデル全体のときは平均値となります。
log=(logloss(0,0.1), logloss(1,0.9) ,logloss(1,0.8) ,logloss(0,0.35)) avg= sum(log)/len(log) print(avg)out> 0.21616187468057912
-
scikit-learnではlog_loss(y_true, y_pred)とモデル全体に対してのLog lossが簡単に求められます。
上記の例はsklearnのDocumentにある例題のspamかhamを1か0に変更したものです。同じ結果が得られています。from sklearn.metrics import log_loss flag=(["spam", "ham", "ham", "spam"]) pre=([.1, .9], [.9, .1], [.8, .2], [.35, .65]) log_loss(flag,pre)out> 0.21616187468057912
まとめ
- モデルの予測確率と結果の乖離を数値化しています。0に近いほどいいモデルといえます。
- 予測確率が大きくハズレた時に評価がより悪化します。たとえば、延滞しない確率が90%の人が延滞した、延滞する確率が80%の人が延滞しなかったなど。
- ブレイアスコアと同様に確率の精度を評価していています。
- モデルを作成する際のベースとなりえる指標となります。ハイパーパラメーターなどを調整する時もこの値が最小値に近いところを選んだりします。
- GridSearchCVなどの評価対象にも使用することができる。
- Log lossの値は別なデータのモデルと数値の大小を比較することはできません。
- 機械学習においてはLog lossとCross-Entropyは同じになります。