本記事はfast.aiのwikiのLog Lossページの要約となります。
筆者の理解した内容で記載します。
一言でいうと、クロスエントロピー。0~1の予測値を入力してモデルの性能を測る指標を出力する。
概要
Logarithmic Lossのこと
分類モデルの性能を測る指標。(このLog lossへの)入力は0~1の確率の値をとる。
この値を最小化したい。完璧なモデルではLog lossが0になる。
予測値が正解ラベルから離れるほどLog lossは増加する。
Accuracyとの違い
- Accuracyは予測した値と正解が一致していた数のカウント。正解/不正解しかないのでいつも良い指標とは限らない(惜しかった、などが測れない)
- Log Lossは実際のラベルからどのくらい違っていたのかを考慮できる
可視化
下記のグラフは正解ラベルが例えば犬=1の場合にLog lossが取りうる値を示す
- 予測値が1に近づくとLog lossはゆっくり減少する
- 予測値が0に近づくと急増する
Log lossはモデルが間違ったラベルを、高い確信度で出力したときに、特に高くなる

コード
pythonの場合。
関数の入力が0~1に収まるようにnp.clip()を通す
import numpy as np
import math
def logloss(true_label, predicted, eps=1e-15):
p = np.clip(predicted, eps, 1 - eps)
if true_label == 1:
return -math.log(p)
else:
return -math.log(1 - p)
数学的なこと
1つの出力値に対するlog lossの計算式を示す。データセットに対してモデルを評価するときは単にすべての出力でlog lossを計算して平均する。
以降で使用する変数の定義
- $N$ : データ数
- $M$ : 全クラスラベル数
- $\log$ : 対数関数(底は$e$)
- $y$ : クラスラベル。0または1をとる。(観測$o$がクラス$c$に属している場合は1を設定している)
- $p$ : モデルによって出力された、観測$o$がクラス$c$に属する確率
2値分類の場合
2値分類(M=2)の場合の式は、
-(y\log p +(1-y)\log(1-p) ) \tag{1}
例1:
クラスラベルが1で予測値0.25が出力されたとき、$(1)$式よりlog lossは
\begin{align}
&-(1\log 0.25 +(1-1)\log(1-0.25) ) \\
&=-(\log 0.25 +0\log(0.75) ) \\
&=-\log0.25
\end{align}
例2:
同様にクラスラベルが0で予測値0.25が出力されたときは
\begin{align}
&-(0\log 0.25 +(1-0)\log(1-0.25) ) \\
&=-(1\log (0.75)) \\
&=-\log(0.75)
\end{align}
*
ちなみに2番目の例は元記事では
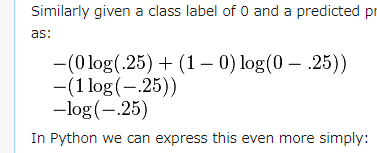
となっており、第二項目のlogの中が$0-.25$と表記されているが、
$(1)$式で第2項目のlogの中身は$1-p$であるのでこれは誤りで、$1-.25$が正しい。
(2019/1/27現在)
多クラスの場合
クラス数M>2の場合、各クラスの予測に関するlog lossの和になる。
-\sum_{c=1}^M y_{o,c} \log(p_{o,c})
log lossに負号がついているのは、
$\log n (0<n<1)$が負の値を返すから。
負号をつけないといつも戻り値が負になって、2つのモデルの性能を比較するときとかによくわからない。
MinMaxルール
上記式$(1)$では、予測値が0または1の時に未定義となるので、予測値の調整をすることがある。
max(min(p, 1−10^−15), 10^-15)
予測値p=0の場合
- min関数を適用。
max(0,10^-15)になる - max関数を適用。
10^-15になる - 予測値0は
10^-15(~0.0000000000000001)
に変換された。
予測値p=1の場合
- min関数を適用。
max(1-10^-15,10^-15)になる - max関数を適用。
1-10^-15になる - 予測値1は
1-10^-15(~0.9999999999999999)に変換された。
Log LossとCross-Entropyは
ほぼ同じものである。
特に機械学習で0~1の範囲で誤り率を計算するときは同じものを解いている。
p \in \bigl\{y, 1-y \bigr\}, q \in \bigl\{ \hat{y}, 1-\hat{y}\bigr\}
とすれば、
H(p,q)=-\sum p_i \log q_i = -y log \hat{y} - (1-y)log(1-\hat{y})
と書くことができ、一致している。
ここで
- $p$: 正解ラベルの集合
- $q$: 予測の集合
- $y$: 真のラベル
- $\hat{y}$: 予測値
である。