- 製造業出身のデータサイエンティストがお送りする記事
- 今回は時系列データを回帰モデル(GBDT)を用いて予測してみました。
はじめに
過去に時系列解析や回帰モデルの手法を整理しておりますので、興味ある方はそちらも参照して頂けますと幸いです。
GBDTの時系列予測
pythonのコードは下記の通りです。
# 必要なライブラリーのインポート
import pandas as pd
import numpy as np
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from matplotlib import pylab as plt
%matplotlib inline
# 統計モデル
import statsmodels.api as sm
# GBDT
from sklearn.ensemble import GradientBoostingRegressor
# グラフを横長にする
from matplotlib.pylab import rcParams
rcParams['figure.figsize'] = 15, 6
# https://stat.ethz.ch/R-manual/R-devel/library/datasets/html/AirPassengers.html
df = pd.read_csv('AirPassengers.csv')
# float型に変換
df['#Passengers'] = df['#Passengers'].astype('float64')
df = df.rename(columns={'#Passengers': 'Passengers'})
# datetime型にしてインデックスにする
df.Month = pd.to_datetime(df.Month)
df = df.set_index("Month")
# データの中身を確認
df.head()
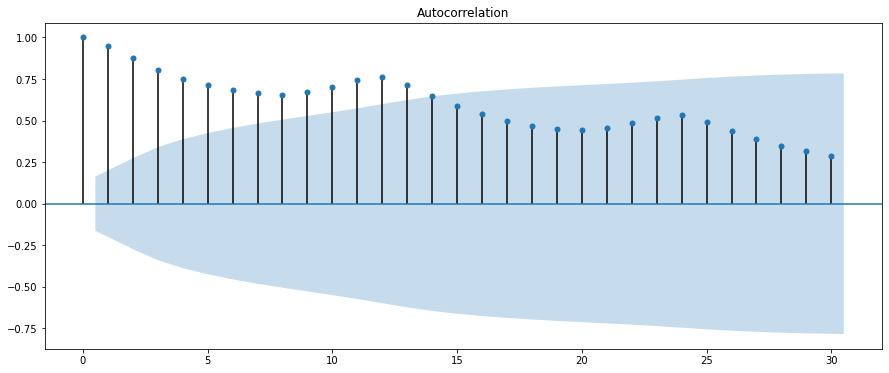
次にコレログラムを作成します。
# 自己相関のグラフ
fig = plt.figure(figsize=(12,8))
fig = sm.graphics.tsa.plot_acf(df["Passengers"], lags=30)
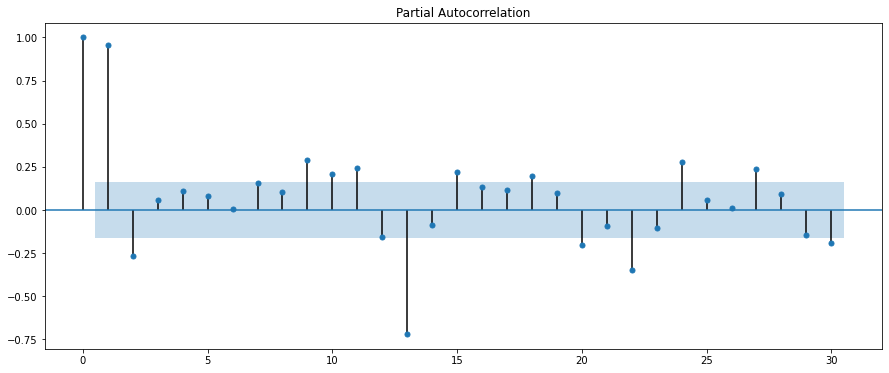
# 偏自己相関を可視化する
fig = plt.figure(figsize=(12,8))
fig = sm.graphics.tsa.plot_pacf(df["Passengers"], lags=20)
今回のデータでは、偏自己相関のグラフを見ると、12ヶ月周期で相関があることが分かるかと思います。つまり、季節的な周期変動があることが分かります。
次に過去12ヶ月の履歴を作成します。
for i in range(1, 13):
df['shift%s'%i] = df['Passengers'].shift(i)
pd.concat([df.head(13), df.tail(3)], axis=0, sort=False)
次に時系列データでよく使用する差分列を作成します。
df['deriv1'] = df['shift1'].diff(1)
df[['Passengers', 'deriv1']].head()
次は2回差分列を作成します。
df['deriv2'] = df['shift1'].diff(1).diff(1)
df[['Passengers', 'deriv2']].head()
最後に統計量も説明変数に追加します。
df['mean'] = df['shift1'].rolling(12).mean()
df['median'] = df['shift1'].rolling(12).median()
df['max'] = df['shift1'].rolling(12).max()
df['min'] = df['shift1'].rolling(12).min()
df[['Passengers', 'mean', 'median', 'max', 'min']][12:24]
これからGBDTで予測をしていきます。
# 欠損値データの削除
df = df.dropna()
df.head()
x = df.drop('Passengers', axis=1)
y = df['Passengers']
# 学習データと評価データを作成
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=1)
# データを標準化
sc = StandardScaler()
sc.fit(x_train) #学習用データで標準化
x_train_std = sc.transform(x_train)
x_test_std = sc.transform(x_test)
# モデルの学習
GBDT = GradientBoostingRegressor()
GBDT.fit(x_train_std, y_train)
# 予測
y_pred = GBDT.predict(x_test_std)
y_ = np.concatenate([np.array([None for i in range(len(y_train))]), y_pred])
y_ = pd.DataFrame(y_, index=df.index)
plt.figure(figsize=(10,5))
plt.plot(y, label='original')
plt.plot(y_, '--', label='predict')
plt.legend()
さいごに
最後まで読んで頂き、ありがとうございました。
今回は時系列データを回帰モデルを用いて予測してみました。
回帰モデルを使用する際は、特徴量作成と選択が重要ですね。
訂正要望がありましたら、ご連絡頂けますと幸いです。