- 製造業出身のデータサイエンティストがお送りする記事
- 今回は製造現場で良く使う時系列データの分析を実施してみました。
時系列データとは
時系列データとは、時間の推移とともに観測されるデータのことを指します。
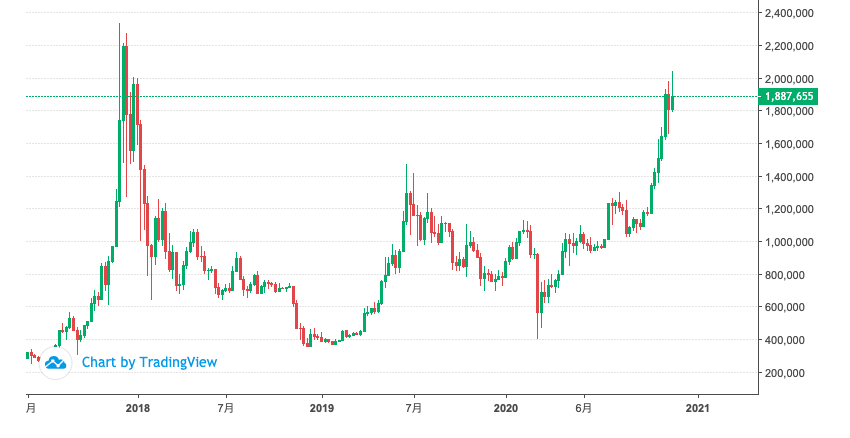
例えば、話題の仮想通貨(ビットコイン)チャートを下記に載せております。株価、為替、仮想通貨、等のチャートは始値、終値、高値、安値のたった4つの値を纏めたものがチャートになります。
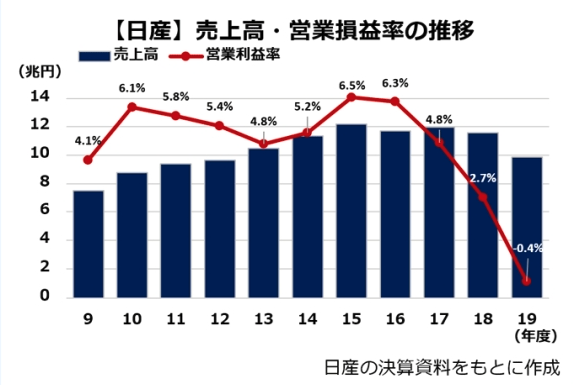
他にも、毎年の売上データなども時系列データです。下記は、日産自動車の売上高と営業損益率の推移を載せております(参考文献:https://monoist.atmarkit.co.jp/mn/articles/2009/30/news063.html)。
今回は時系列分析の中でも、「予測」に焦点を当てて解析を行っていこうと思います。
時系列解析
今回は、3つの手法(移動平均モデル:MA、自己回帰モデル:AR、自己回帰移動平均モデル:ARMA)を実装していこうと思います。
1.移動平均モデル(MA:Moving Average model)
解析したい時系列データに対して、ある時点tのデータと過去のデータで平均を取る手法になります。数式は下記のようになります。
\begin{eqnarray}
y_t = c + ε_t + θ_{1}ε_{t-1} + ・・・ + θ_{q}ε_{t-q}
\end{eqnarray}
$ε_t$ : $W.N(σ^2)$(分散$σ^2$のホワイトノイズ)
$c$ : 定数
$θ$ : 定数
$ε$ : 時点$t$におけるノイズ
pythonのコードは下記の通りです。
# 必要なライブラリーのインポート
import pandas as pd
import numpy as np
# 統計モデル
import statsmodels.api as sm
from matplotlib import pylab as plt
%matplotlib inline
# グラフを横長にする
from matplotlib.pylab import rcParams
rcParams['figure.figsize'] = 15, 6
# データの読み込み
# https://stat.ethz.ch/R-manual/R-devel/library/datasets/html/AirPassengers.html
df = pd.read_csv('AirPassengers.csv')
# float型に変換
df['#Passengers'] = df['#Passengers'].astype('float64')
df = df.rename(columns={'#Passengers': 'Passengers'})
# datetime型にしてインデックスにする
df.Month = pd.to_datetime(df.Month)
df = df.set_index("Month")
# データの中身を確認
df.head()
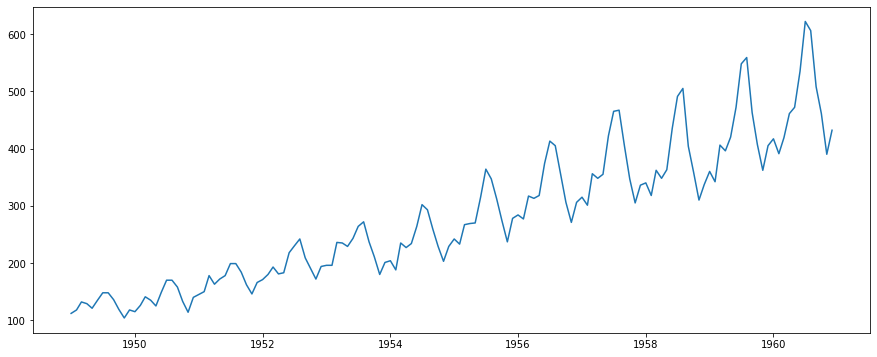
# データの可視化
plt.plot(df.earnings)
今回使用したデータは、月ごとの飛行機の乗客数データです。対象期間は1949年1月から1960年12月です。
初出は「Box, G. E. P., Jenkins, G. M. and Reinsel, G. C. (1976) Time Series Analysis, Forecasting and Control. Third Edition. Holden-Day. Series G.」となります。
URLから、データの詳細を確認できます。
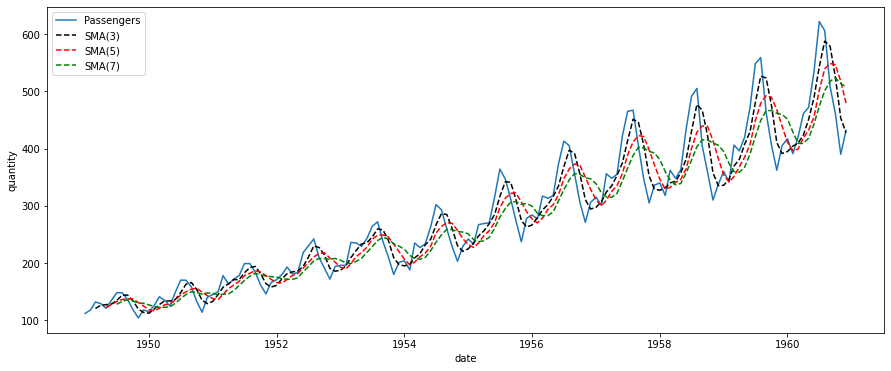
次に移動平均を求めてみたいと思います。
# 移動平均
df["3ma"]=df["Passengers"].rolling(3).mean().round(1)
df["5ma"]=df["Passengers"].rolling(5).mean().round(1)
df["7ma"]=df["Passengers"].rolling(7).mean().round(1)
# 可視化
plt.plot(df["Passengers"], label="Passengers")
plt.plot(df["3ma"], "k--", label="SMA(3)")
plt.plot(df["5ma"], "r--", label="SMA(5)")
plt.plot(df["7ma"], "g--", label="SMA(7)")
plt.xlabel("date")
plt.ylabel("quantity")
plt.legend()
plt.show()
2.自己回帰モデル(AR:Autoregressive Integrated Moving model)
解析したい時系列データがあるとき、そのデータの過去のデータに回帰させて未来の値を算出するモデルです。数式は下記のようになります。
\begin{eqnarray}
y_t = c + φ_1y_{t-1} + ・・・ + φ_py_{t-p} + ε_t
\end{eqnarray}
$ε_t$ : $W.N(σ^2)$(分散$σ^2$のホワイトノイズ)
$y_t$ : 時点$t$における時系列でーたの値
$c$ : 定数
$φ$ : 定数
$ε$ : 時点$t$におけるノイズ
まず初めに自己相関係数を推定してみたいと思います。自己相関とは前期と今期がどれだけ似ているかを表す数値になります。
# 自己相関を求める
df_acf = sm.tsa.stattools.acf(df["Passengers"], nlags=30)
# 自己相関のグラフ
fig = plt.figure(figsize=(12,8))
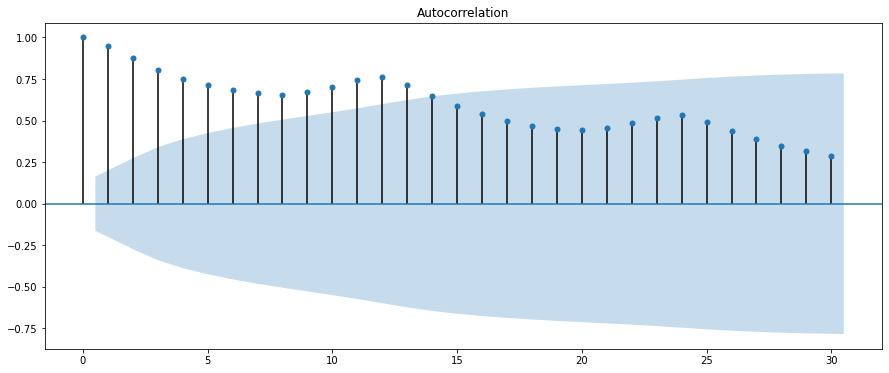
fig = sm.graphics.tsa.plot_acf(df["Passengers"], lags=30)
結果の見方は、薄青の空間は、真に自己相関がない場合の信頼区間95%の範囲を示します。
つまり、この範囲外の値を持つlag地点に(統計的に)有意な自己相関があると分かります。
今回の結果であれば、正の自己相関がありますので、先月の乗客数が多ければ、今月も多いということがわかります。
予測を行う際は、モデル選択において自己相関ではなく、偏自己相関を見る必要があります。
一次の自己相関がある時、
1.昨日の値が今日の値に関係する
2.一昨日の値が昨日の値に関係ある
→一昨日の値が今日の値に関係あるという関係が導けます(推移律)。
そこで、本当に高次の自己相関があるのかを見るためには、注目する変数以外の影響を取り除いて自己相関を図る必要があり、それが偏自己相関で見ることができます。
# 偏自己相関を求める
df_pacf = sm.tsa.stattools.pacf(df["Passengers"], nlags=20, method='ols')
# 偏自己相関を可視化する
fig = plt.figure(figsize=(12,8))
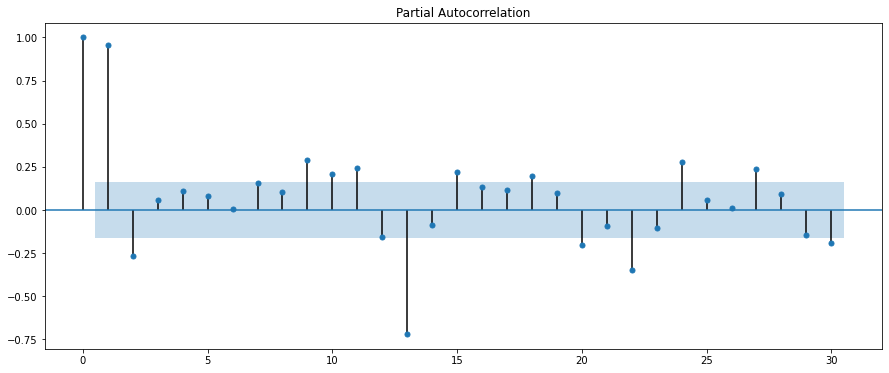
fig = sm.graphics.tsa.plot_pacf(df["Passengers"], lags=20)
今回のデータでは、偏自己相関のグラフを見ると、12ヶ月周期で相関があることが分かるかと思います。つまり、季節的な周期変動があることが分かります。
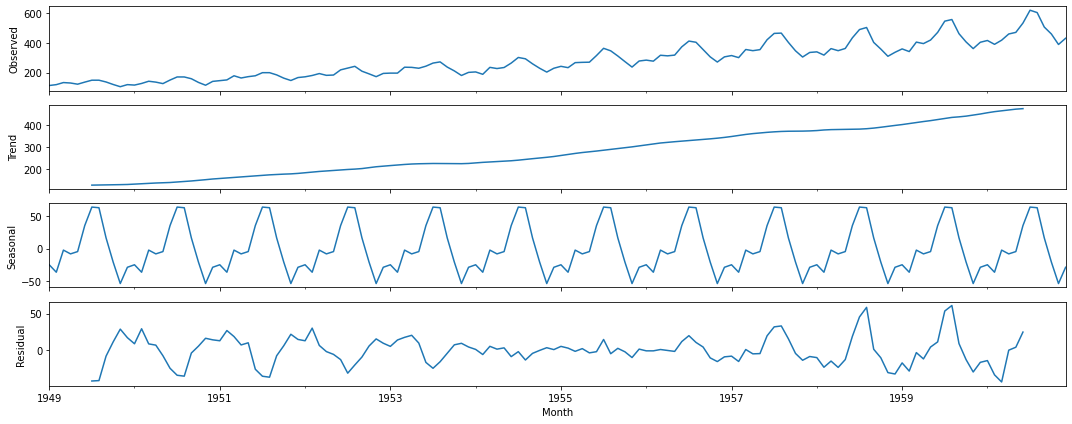
次は、トレンド、季節性、残差に分解してみようと思います。
res = sm.tsa.seasonal_decompose(df["Passengers"])
fig = res.plot()
最後にARモデルの推定を行いたいと思います。
まず作成した関数は下記です。
def invert(data, diff, prepro):
"""前処理に応じた逆変換をする
Parameters
----------
data (np.array or np.float) : 原系列のデータ
diff (np.array or np.float) : 変換したデータ
prepro (str) : 前処理の手法('diff', 'pct', 'logdiff')
"""
if prepro == 'diff':
return data + diff
elif prepro == 'pct':
return data * diff + data
elif prepro == 'logdiff':
return np.exp(diff) * data
else:
print('{}は対応していない前処理です'.format(prepro))
return None
def invert_predict(data, pred, start, prepro, period, span=None):
"""前処理した系列の予測値を原系列に逆変換する
Parameters
----------
data (np.array) : 実測値
pred (np.array) : 予測値
start (int) : 逆変換して得る最初の期
prepro (str) : 前処理手法('diff', 'pct', 'logdiff')
period (int) : 何期先まで予測したか
xlim (turple) : 原系列グラフのx軸の描画範囲
ylim (turple) : 原系列グラフのy軸の描画範囲
"""
pred_inverted = np.empty_like(pred)
if span == None:
pred_inverted[0] = invert(data[start - 1], pred[0], prepro)
for i in range(1, period):
pred_inverted[i] = invert(pred_inverted[i - 1], pred[i], prepro)
else:
for i in range(span):
pred_inverted[i, 0] = invert(data[start - period + i], pred[i, 0], prepro)
for j in range(1, period):
pred_inverted[i, j] = invert(pred_inverted[i, j-1], pred[i, j], prepro)
return pred_inverted
def plot_processed_series(data, pred, start, data_num, interval, prepro, axis):
"""前処理した系列の実測値及び予測値をグラフに書き出す
Parameters
----------
data (np.array) : 実測値
pred (np.array) : 予測値
start (int) : プロットの最初の期
data_num (int) : 予測に使用したデータの数
interval (int) : プロットする区間の長さ
prepro (str) : 前処理手法('diff', 'pct', 'logdiff')
axis (matplotlib.axes.Axes) : 書き出したいグラフのAxesオブジェクト
"""
if prepro == 'diff':
target = data.diff().values
elif prepro == 'pct':
target = data.pct_change().values
elif prepro == 'logdiff':
target = (np.log(data) - np.log(data.shift(1))).values
axis.plot(np.arange(start-data_num, start), target[start-data_num:start], marker='.')
axis.plot(np.arange(start, start+interval), target[start:start+interval], c='green', label='Actual', marker='.')
axis.plot(np.arange(start, start+interval), pred, c='r', label='Predict', marker='.')
axis.set_ylabel('diff', fontsize=17)
axis.legend()
return None
def plot_original_series(data, pred, start, interval, axis, xlim, ylim):
'''逆変換した系列の実測値および予測値をグラフに書き出す.
Parameters
----------
data (np.array) : 実測値
pred (np.array) : 予測値
start (int) : プロットの最初の期
interval (int) : プロットする区間の長さ
axis (matplotlib.axes.Axes) : 書き出したいグラフのAxesオブジェクト
xlim (turple) : 原系列グラフのx軸の描画範囲
ylim (turple) : 原系列グラフのy軸の描画範囲
'''
axis.plot(np.arange(1, start+interval+1), data[:start+interval], c='green', label='Actual', marker='.')
axis.plot(np.arange(start+1, start+interval+1), pred, c='r', label='Predict', marker='.')
axis.set_xlim(xlim)
axis.set_ylim(ylim)
axis.set_ylabel('Passengers', fontsize=17)
axis.legend()
return None
def plot_predict(data, pred, start, data_num, prepro, xlim=None, ylim=None):
"""AR(MA)モデルで予測したデータからグラフを描画する
Parameters
----------
data (np.array) : 実測値
pred (np.array) : 予測値
start (int) : プロットを始める期( > data_num)
data_num (int) : データをいくつ利用したか
prepro (str) : データの前処理方法('diff', 'pct', 'logdiff')
xlim (turple) : 原系列グラフのx軸の描画範囲
ylim (turple) : 原系列グラフのy軸の描画範囲
"""
period = len(pred) #何期先までの予測をしたか
# 逆変換して原系列の予測を用意
pred_inverted = invert_predict(data, pred, start, prepro, period)
# 処理した系列、原系列について実測値と予測値の比較
fig, axes = plt.subplots(1, 2, figsize=(12, 5))
plt.rcParams["font.size"] = 12
plt.subplots_adjust(wspace = 0.3)
plot_processed_series(data, pred, start, data_num, period, prepro, axes[0])
plot_original_series(data, pred_inverted, start, period, axes[1], xlim, ylim)
plt.show()
return None
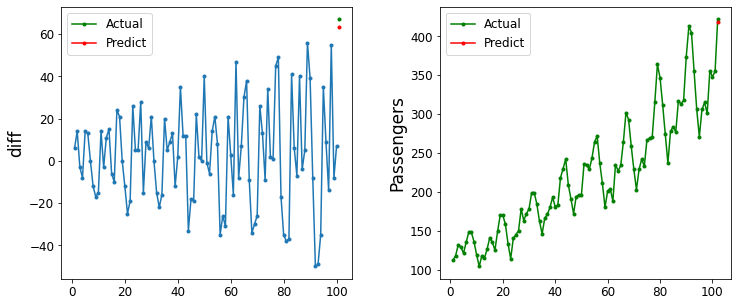
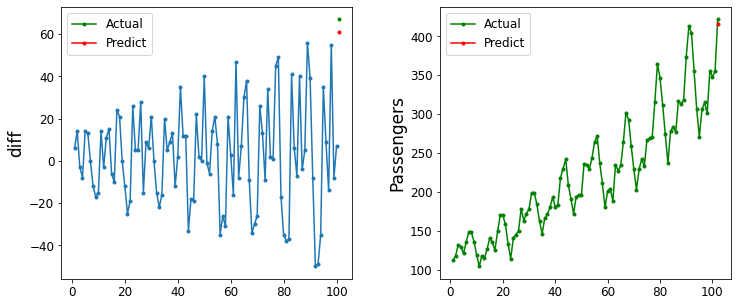
今回は100ヶ月のデータを使ったAR(12)で1ヶ月後の飛行機の乗客数を予測してみようと思います。
target = df["Passengers"].diff().values
start = 101
period = 1
data_num = 100
pred = sm.tsa.AR(target[start-data_num:start]).fit(maxlag=12).predict(start=data_num, end=data_num+period-1)
plot_predict(df["Passengers"], pred, start, data_num, 'diff')
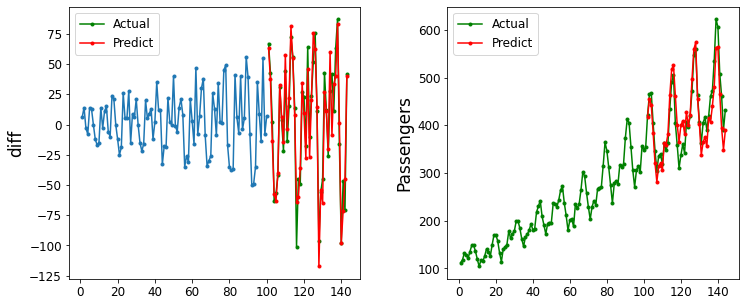
ちなみに最後までを予測しようとしたら下記のようになります。
start = 101
period = 1
data_num = 100
pred_seq = np.arange(start+period-1, len(df))
pred = np.empty((len(pred_seq), period), dtype=float)
for i, j in enumerate(pred_seq):
pred[i] = sm.tsa.AR(target[j-period+1-data_num:j-period+1]).fit(maxlag=12).predict(start=data_num, end=data_num+period-1)
plot_predict(df["Passengers"], pred, start, data_num, 'diff')
3.自己回帰移動平均モデル(ARMA)
ARMAモデルは現在の値$𝑦_𝑡$を過去の値とホワイトノイズの和によって表現するモデルです。ARモデルとMAモデルから構成されるモデルと考えることもできます。数式は下記のようになります。
\begin{eqnarray}
y_t = c + φ_1y_{t-1} + ・・・ + φ_py_{t-p} + ε_t+ θ_{1}ε_{t-1} + ・・・ + θ_{q}ε_{t-q}
\end{eqnarray}
$ε_t$ : $W.N(σ^2)$(分散$σ^2$のホワイトノイズ)
$y_t$ : 時点$t$における時系列でーたの値
$c$ : 定数
$θ$ : 定数
$φ$ : 定数
$ε$ : 時点$t$におけるノイズ
基本的にはARモデルと一緒ですので、コードと結果だけ下記に載せていきます。
target = df["Passengers"].diff().values
start = 101
period = 1
data_num = 100
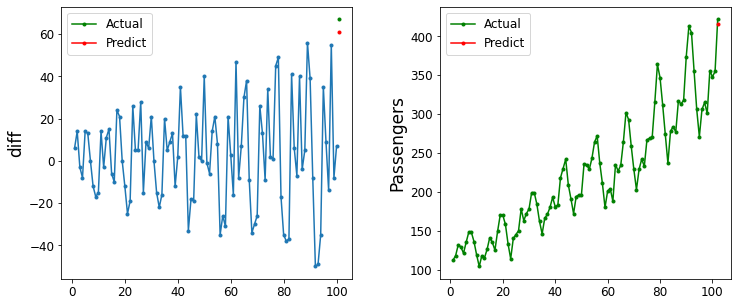
pred = sm.tsa.ARMA(target[start-data_num:start], order=(9, 3)).fit().predict(start=data_num, end=data_num+period-1)
plot_predict(df["Passengers"], pred, start, data_num, 'diff')
target = df["Passengers"].diff().values
start = 101
period = 1
data_num = 100
pred = sm.tsa.ARMA(target[start-data_num:start], order=(9, 3)).fit().predict(start=data_num, end=data_num+period-1)
plot_predict(df["Passengers"], pred, start, data_num, 'diff')
ARMA関数を用いて係数を推定しようとするとき、statsmodelsでARMAを推定する際下記のようなエラーが出ることがあります。
- ValueError:The computed initial AR coefficients are not stationary
- MA coefficients are not invertible
これはARMA過程が定常性を仮定している一方で、データが定常性を満たさない等の場合に最適化のための初期値を上手く設定できないことが原因で起こります。
今回でいえば、12ヶ月の周期性があるまま推定しようとしているので、前処理をきちっとやる必要があります。対処法としては下記がありますので、ご参考までに記載しておきます。
- fit()の引数start_paramsを用いて手動で初期値を設定する
- fit()の引数trend='nc'を用いる
- fit()の引数にmethod='mle'を用いる ※初期値の推定方法を変更する
- データが定常性を満たすように変換する ※これが一番良いです
さいごに
最後まで読んで頂き、ありがとうございました。
今回は時系列解析を実装してみました。
他にも手法はたくさんありますので、別の機会に実装してみようと思います。
訂正要望がありましたら、ご連絡頂けますと幸いです。